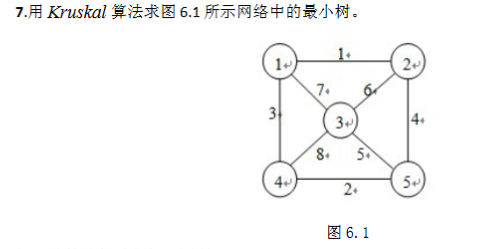
最小树问题

一般研究无向图；

树图：倒置的树，根(root)在上，树叶(leaf)在下；

多级辐射制的电信网络、管理的指标体系、家谱、分类学、组织结构等都是典型的树图。 

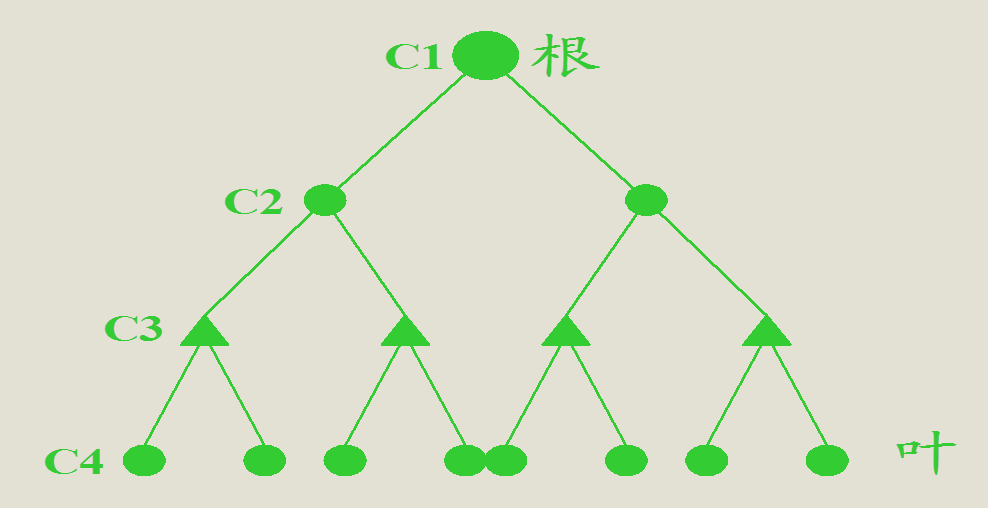
树 的 概 念

无圈连通图称为树(tree)，记为T；

例：判断下面图形哪个是树；

“破圈法”基本步骤

破 圈 法

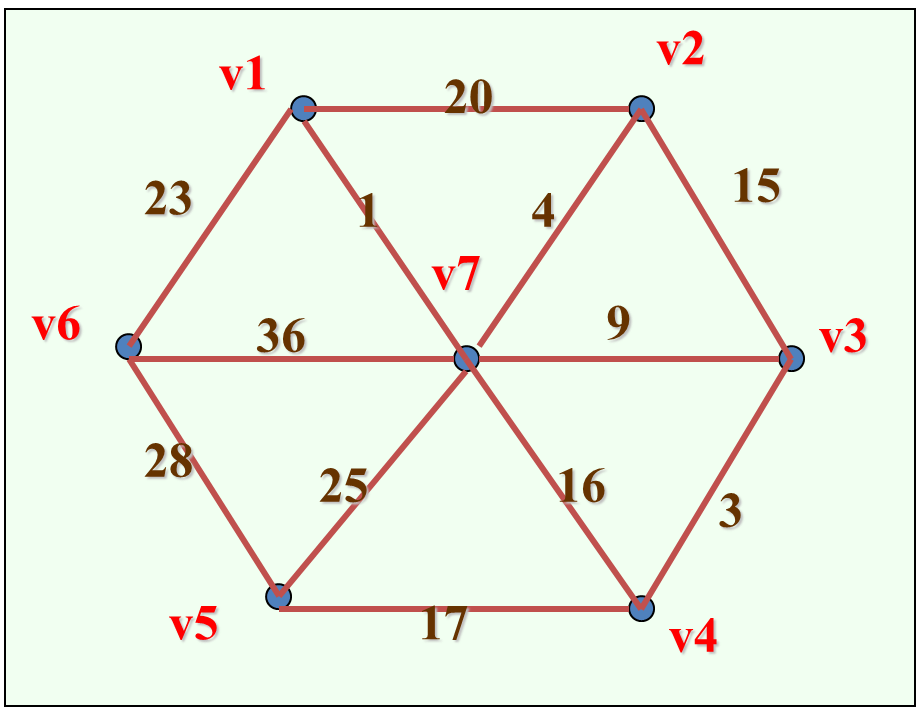
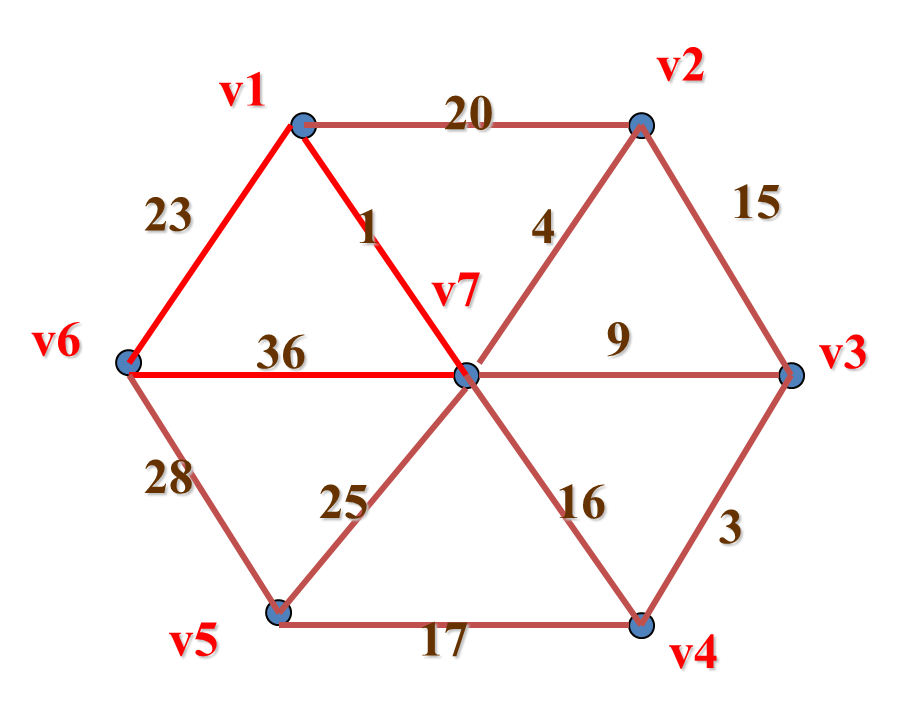
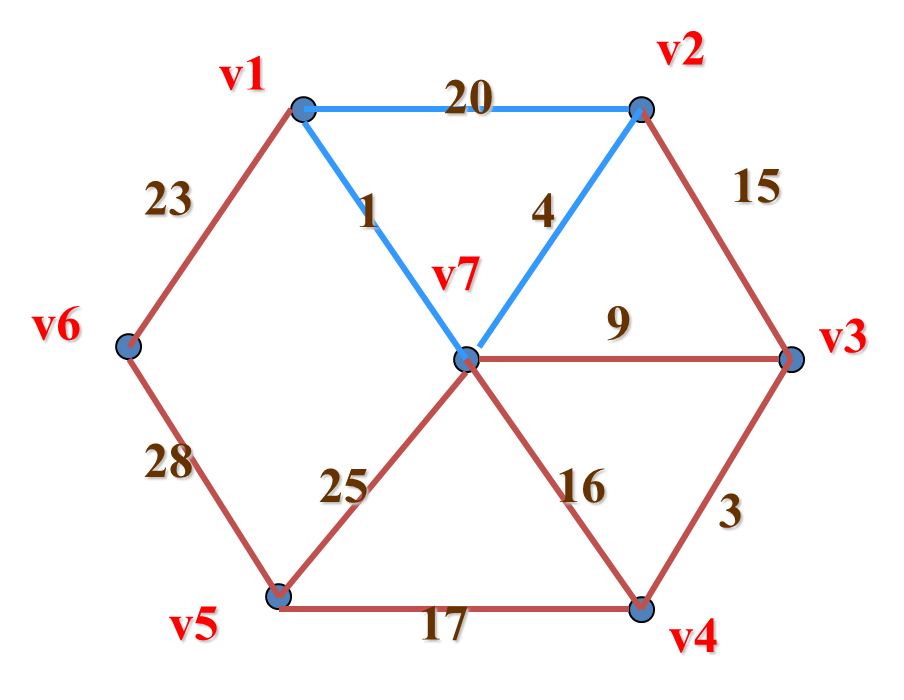
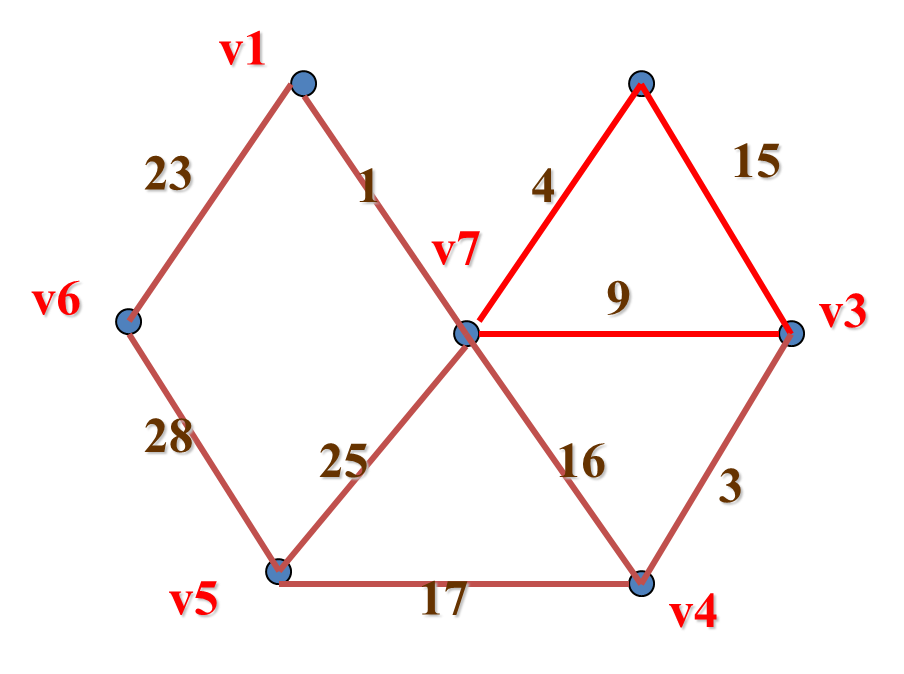
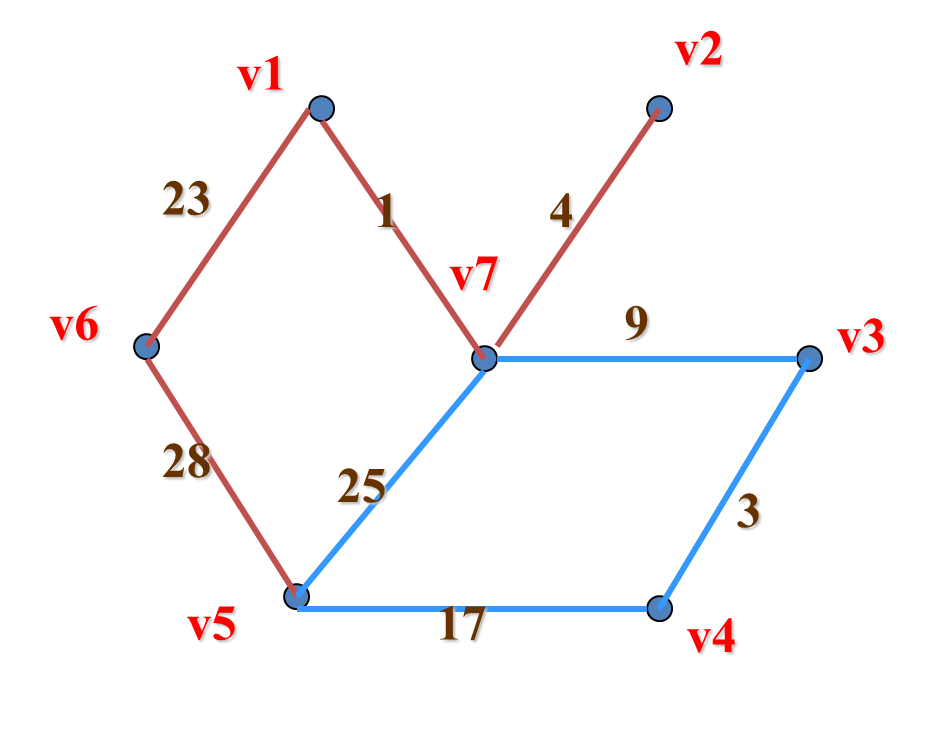
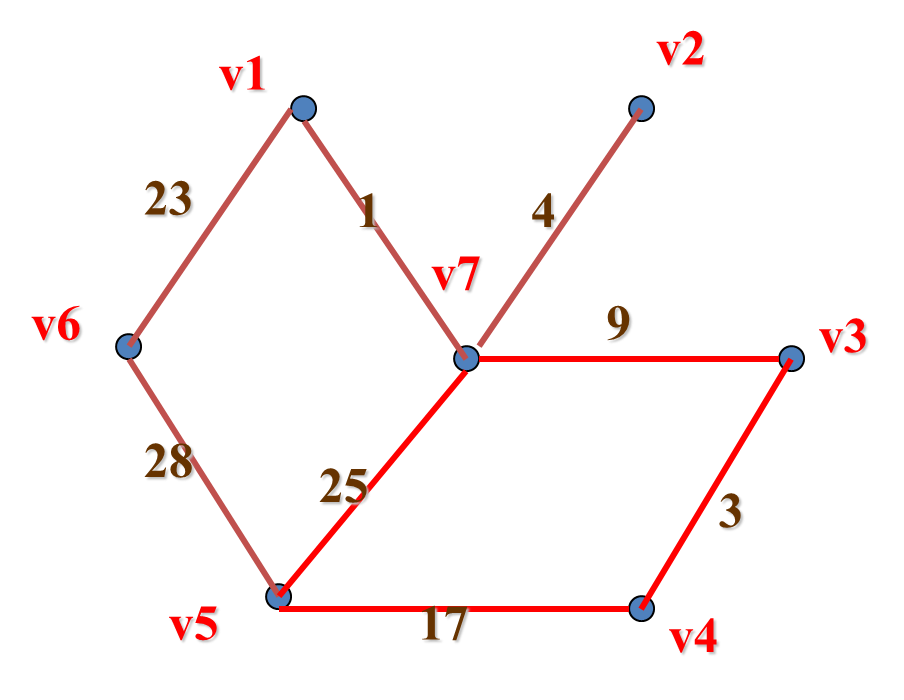
先从图G任取一个圈，并从圈中去掉一条权最大的边。若在同一圈中有几条都是权最大边，则任选其中一边去掉。

“避圈法”基本思想

开始选一条最小的边，以后每步从未选的边中选取一条权最小的边，使它与已选边不构成圈，直至选够q-1条边至。