一、实验目的

1．了解电阻应变测试技术的基本原理，学会使用应力/应变综合参数测试仪测量应变。

2．测定矩形截面梁纯弯曲时横截面上的正应力分布规律，验证梁的平面弯曲正应力公式。

3．测定材料的泊松比。

二、实验仪器

1．材料力学多功能试验台

2．应力/应变综合参数测试仪

三、实验原理

    在平面弯曲时，梁横截面上正应力公式为：

    式中：M为作用在横截面上的弯矩；I为梁横截面对中性轴的惯性矩； y为中性轴到测点之距；

    上式是在纯弯曲条件下，根据平截面假定和纵向纤维互不挤压等假设的条件下推导出来的。它表明梁横截面上正应力沿高度按线性规律分布。这一结论是否正确？可否应用于工程实践中？需要通过实验来验证。

    选取一具有纵向对称面的矩形截面简支梁，在距两端等距的两个截面上施加大小相等的作用力F/2，使梁中部承受纯弯曲，在纯弯段内沿梁高等距分布粘贴五枚应变片，使应变片轴线与梁轴线平行，在梁上表面贴一枚与轴线垂直的应变片以测定横向应变。

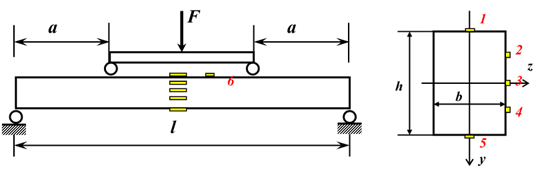
用XL－2118B应力/应变综合参数测试仪测出各应变片的应变值，如果所加载荷能保证梁在弹性条件下工作，则由虎克定律可求得各测点的应力值，即：

式中：E为材料的弹性模量。E=206 GPa。为提高测量精度，采用“增量法”，每增加一次载荷ΔF  ，测出相应应变的增量，最后取应变增量的平均值Dε，求出各测点的应力增量值：

              Ds_实＝E×Dε

    把由实验得到的Ds_实，与由理论计算得到的 Ds_理＝DM×y/I进行比较，以验证弯曲正应力公式的正确性。

四、实验步骤

1.  确定梁的尺寸b=20mm, h=40mm, l=620mm, a=135mm；计算I；检查梁支点，加载点位置是否正确。

2.  接线：将六个应变片和温度补偿片接入应变仪各测点。其中工作片接AB，补偿片接BC(公共补偿)。

3.  打开XL－2118B应力/应变综合参数测试仪，按“N/kg”转换键使力显示单位为N，检查螺旋加载装置，确认无力作用后按“清零”键。

4.  预调平衡：按单点平衡键，对各测点进行桥路平衡。

5.  加载测量：记录各测点应变片的读数ε_i 。

6.  卸载，数据经教师审阅后方可离开。

五、实验数据处理

1. 将实验中载荷、应变、尺寸记入实验报告中；

2. 计算：Ds_实＝E×Dε；Ds_理＝DM×y/I (其中ΔM＝ΔF×a/2 )

3. 以应力为横坐标，梁的高度为纵坐标，画出实测应力与理论应力随梁高度的变化曲线，并进行比较分折

六、分析讨论题

1. 影响实验结果的主要因素有哪些?

2. 尺寸完全相同的钢梁和木梁，如果距中性层等远处，纵向纤维伸长量对应相等，问两梁相应截面的应力是否相同?为什么?

3. 为什么要进行温度补偿?如何补偿。

虚拟仿真实验网址：力学实验

教师讲解

虚拟仿真实验演示