惯性矩的平行移轴公式

图示平面图形面积为A，C为形心，yC、zC为过形心C的坐标轴，yC与y平行，相距a；zC与z平行，相距b；则有：

上式即为惯性矩（积）的平行移轴公式。

证明：根据惯性矩和极惯性矩的定义有

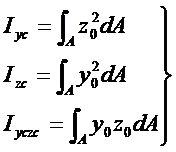
利用坐标变换关系

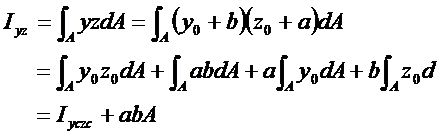
由上式可见，图形对于形心轴的惯性矩是对所有平行轴的惯性矩中最小的一个。在应用平行移轴公式时，要注意应用条件，即y_c、z_c轴必须是通过形心的轴，且y、z轴必须分别与y_c、z_c轴平行。在计算惯性积时，还须注意a、b的正负号，它们是截面形心C 在Oyz坐标系中的坐标值。

惯性矩的转轴公式

当一对坐标轴绕原点转动时，截面对于不同坐标轴的惯性矩或惯性积之间有一定的关系，即所谓的转轴公式。用它可以确定截面的主惯性轴及计算截面的主惯性矩。

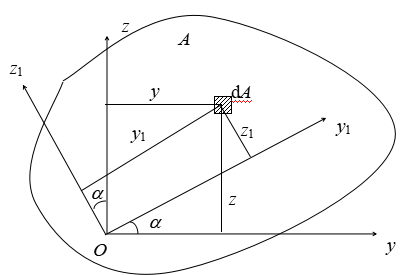
(1) 角度α的正负号，从原坐标轴y,z转至新坐标轴y1,z1，以逆时针转向为正。

(2) 原点O为截面图形平面内的任意点，转轴公式与图形的形心无关。

(3) 图形对通过同一坐标原点任意一对相互垂直坐标轴的两个轴惯性矩之和为常量，等于图形对原点的极惯性矩，即

主惯性轴、主惯性矩  

任意形状截面图形对以某一点O为坐标原点的坐标轴y0、z0的惯性积为零（），则坐标轴y0、z0称为图形通过点O的主惯性轴。截面图形对主惯性轴的惯性矩、称为主惯性矩。

对于某一点O，若能找到通过点O的图形的对称轴，则以点O为坐标原点，并包含对称轴的一对坐标轴，即为图形通过点O的一对主惯性轴。对于具有对称轴的图形（或组合图形），往往已知其通过自身形心轴的惯性矩。于是，图形对通过点O的主惯性轴的主惯性矩，一般即可由平行移轴公式直接计算。

若通过某一点O没有图形的对称轴，则可以点O为坐标原点，任作一坐标轴y,z为参考轴，并求出图形对参考轴y,z的惯性矩和惯性积。于是，图形通过点O的一对主惯性轴方位及主惯性矩分别为

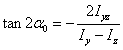
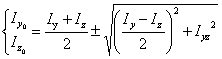
主惯性轴、主惯性矩的特征：

（1）图形通过某一点O至少具有一对主惯性轴，而且主惯性矩是图形对通过同一点O所有轴的惯性矩中的最大值和最小值。

（2）主惯性轴的方位角，从参考轴y,z算起，以逆时针转向为正。

（3）若图形对一点O为坐标原点的两主惯性矩相等，则通过点O的所有轴均为主惯性轴，且所有主惯性矩都相同。

（4）以截面图形形心为坐标原点的主惯性轴，称为形心主惯性轴。图形对一对形心主惯性轴的惯性矩，称为形心主惯性矩。

在对构件进行强度、刚度和稳定计算中，常常需要确定形心主轴和计算形心主惯性矩。因此，确定形心主轴的位置是十分重要的。

由于图形对包括其对称轴在内的一对正交坐标轴的惯性积为零，所以对于具有对称轴的截面图形，可根据图形具有对称轴的情况，确定形心主轴的位置。如果图形有一个对称轴，则此轴必定是形心主轴、而另一形心主轴通过形心，并与对称轴垂直；如果图形有两个对称轴，则该两轴都为形心主轴；如果图形具有3个或更多对称轴，过图形形心的任何轴都是形心主轴，且图形对其任一形心主轴的惯性矩都相等。