1．惯性矩

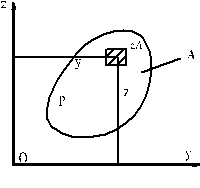
定义：面积对坐标轴的二次矩。

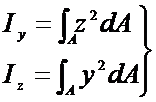
（1）惯性矩恒为正值。

（2）量纲为长度的4次方。

2．惯性半径

力学计算中，有时把惯性矩写成图形面积A与某一长度二次方的乘积，即

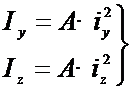
则有：

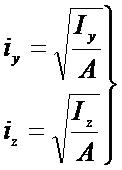
i_y为图形对y轴的惯性半径，i_z为图形对z轴的惯性半径，量纲为长度。

3．极惯性矩

定义：极惯性矩（又称截面二次极矩）是面积对于坐标原点（极点）的二次矩。

极惯性矩与横截面形状和尺寸有关，是计算抗扭截面系数的一个重要物理量。

极惯性矩与惯性矩的关系：

平面图形对任一点的极惯性矩，等于图形对通过此点且在其平面内的任一对正交轴惯性矩之和。

4．组合图形惯性矩的计算

当平面图形由若干个简单图形组成时，根据惯性矩的定义，可以先算出每个简单图形对某一轴的惯性矩，然后求其总和即整个图形对同一轴的惯性矩。

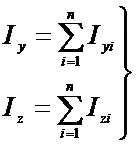
5. 惯性积

定义：

（1）由于yz乘积可正、可负、可为零，因此惯性积I_yz值可正、可负、可为零。

（2）量纲为长度的四次方。

（3）y、z轴中只要有一轴为对称轴，则I_yz=0