欧拉公式的适用范围

压杆处于临界状态时横截面上的平均应力称为压杆的临界应力，压杆的临界应力就是临界力除以原始横截面面积。

根据细长压杆临界压力的欧拉公式可求得临界应力为   

由截面的几何性质

i为截面惯性半径，引入参数 

λ称为压杆的柔度或压杆的长细比，它是一个无量钢量，集中反映了压杆的长度、约束条件、截面尺寸、形状对临界应力的影响。

因此临界应力可由下式计算

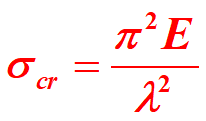
此式称为压杆临界应力的欧拉公式。欧拉公式导出利用了弯曲变形的微分方程，而材料服从胡克定律是微分方程的基础，因此公式的适用范围是临界应力小于等于材料的比例极限。

求出与比例极限对应的柔度λ_1，公式的适用范围可用下式表示。

满足此式的压杆称为细长杆或大柔度杆，这就是欧拉公式的适用范围。需要说明的是λ₁也称为第一界限柔度，由公式可知它与材料性质有关，即不同的材料λ₁不同。

中柔度杆（中长杆）

若λ<λ₁，临界应力σ_cr会大于材料的比例极限，欧拉公式已不能适用。属于超过比例极限σ_p的压杆稳定问题。一般采用直线形式的经验公式。：

σ_cr=a－bλ

式中a、b为与材料有关的常数。

经验公式的适用范围是：      

sp ≤s ≤ss 

前面已经求出与比例极限对应的柔度，即第一界限柔度，下面计算与屈服强度对应的柔度，即第二界限柔度λ₂：

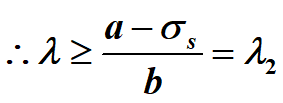
满足 λ₂<λ≤λ₁的压杆称为中柔杆或中长杆 。

小柔度杆（短粗杆）

当λ≥λ₂时，压杆的临界应力已达到材料的屈服强度，这时压杆的失效实际为强度失效，因此 此时的临界应力就等于屈服强度。满足这一条件的压称为小柔度杆或短粗杆。

临界应力总图

综上所述，临界应力σ_cr随压杆柔度λ而不同，即不同的柔度，临界应力σ_cr应按相应的公式来计算。

临界应力σ_cr随柔度λ变化的图线称为临界应力总图。

需要说明的是，失稳是考虑杆的整体变形，局部削弱（如螺钉孔等）对整体变形影响很小，计算A、I时可忽略削弱的尺寸。