两端铰支细长压杆的临界压力

设两端为球铰的细长压杆处于微弯平衡，选取坐标系如图所示，距原点为x的任意截面的挠度为w，弯矩为Fw，当w为正时，M为负，w为负时，M为正，即M与w的符号相反。

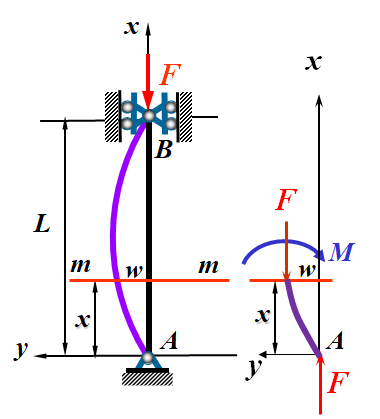
M=-Fw

挠曲线近似微分方程

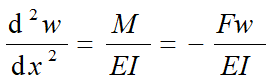
引入 ，则：

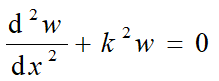
微分方程的通解为：w=Asinkx+Bcoskx，A、B为积分常数，由边界条件确定。

当x=0时，w=0，则：B=0；当x=l时，w=0，则： Asinkl=0。

（1）显然A≠0，若A=0，则w=0，杆始终为直线，这与微弯假设前提矛盾。

（2）故只有sinkl=0，于是

kl=0,π,2π,3π……或kl=nπ（n=0,1,2……）

故 

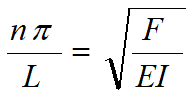
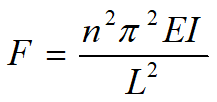
由此可见，使曲线保持平衡时，压力为出现多值。使压杆保持微弯平衡时的最小压力即为临界压力，故取n=1，则

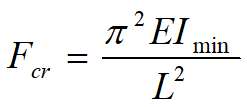
此式即为两端铰支细长压杆的欧拉公式。

压杆将绕惯性矩最小的轴弯曲，故公式中I值为最小值。

由w=Asinkx 知挠曲线的形状为正弦曲线 。当当n=1时，为一个半波正弦曲线；当n=2时，为2个半波正弦曲线；当当n=3时，为3个半波正弦曲线。当在高阶临界压力下，压杆变形成2个、3个……半波正弦曲线，其形式是不稳定的，只有当中间有约束时，才能转为稳定。

欧拉公式的应用条件：

（1）理想压杆（轴线为直线、压力与轴线重合、材料均匀）；

（2）线弹性范围内；

（3）两端为球铰支座。

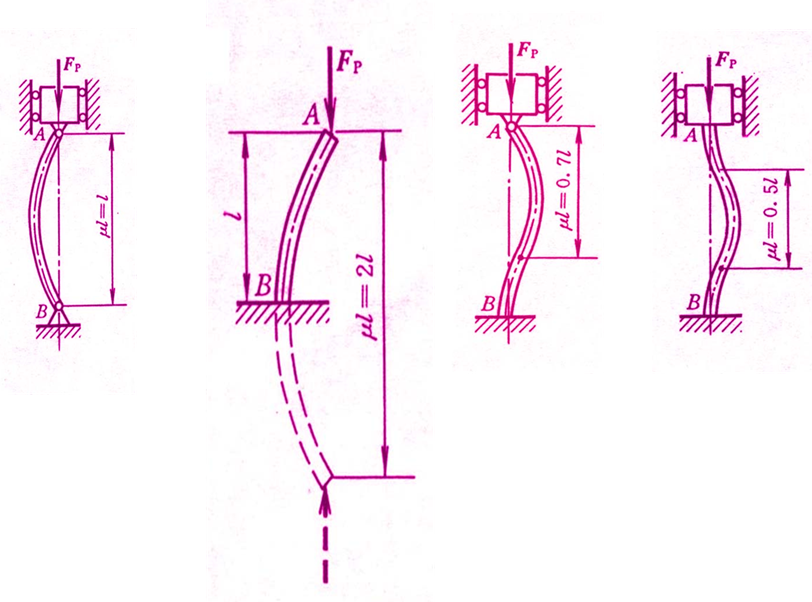
细长压杆临界力欧拉公式的一般形式

μ—长度系数（或约束系数）。μl——相当长度。

一端自由，一端固定: μ＝2.0

一端铰支，一端固定: μ＝0.7

两端固定: μ＝0.5

两端铰支: μ＝1.0