杆件同时受横向力和轴向力的作用

外力分析：

将力F分解为轴向力和横向力，分别引起轴向拉伸和平面弯曲变形。

内力分析：

画出轴力图和弯矩图，确定危险截面为固定端截面。

应力分析：

画出危险截面上的应力分布图，确定危险点的位置。

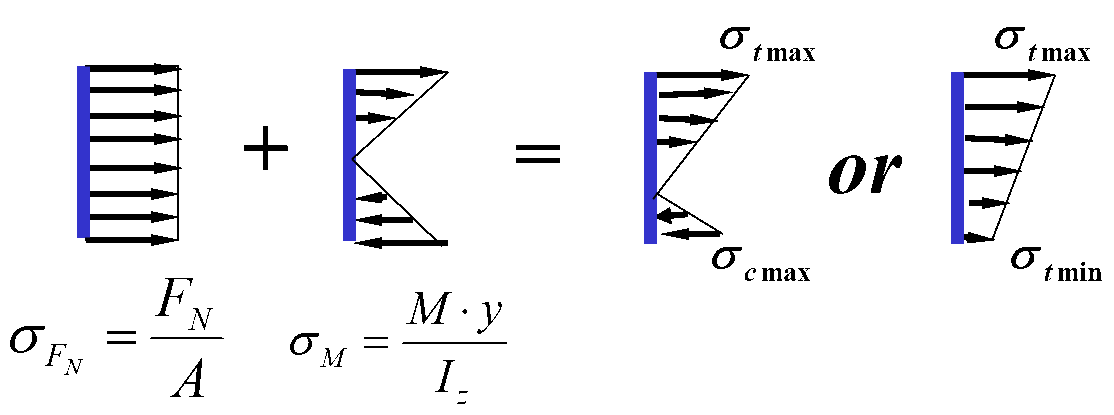
强度条件：

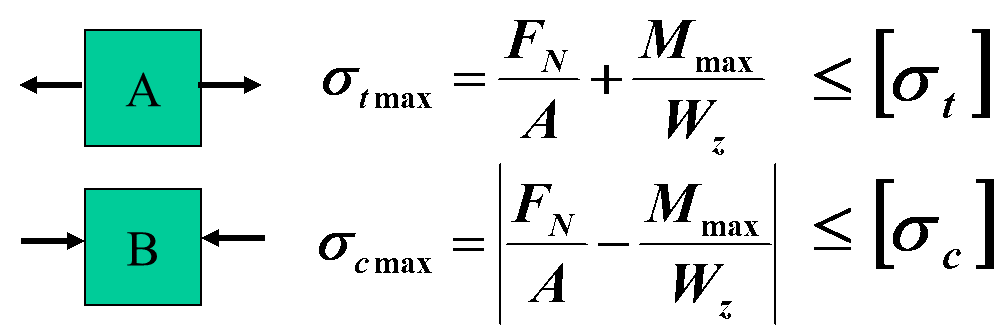
偏心拉压问题

如果外力的作用线平行于杆件的轴线，但不通过横截面的形心，则引起偏心拉伸(或压缩)，简称偏心拉压。当外力在纵向对称面时，称为单向偏心拉压。在工程实际中，经常会遇到单向偏心拉压的问题，如图中开口链环和厂房的立柱。如果将载荷向杆件等直部分AB段的轴线平移，则作用在AB 段上的外力可视为轴向力P和矩为Pe的力偶，轴向力可使杆段产生拉伸(或压缩)，力偶将使杆段产生弯曲，所以，偏心拉压本质上是轴向拉压与弯曲的组合变形问题。

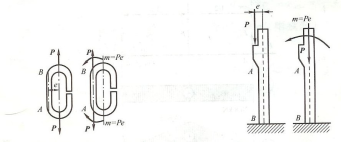
偏心拉伸图                     偏心压缩图

下面以矩形截面杆为例，说明单向偏心拉压的应力计算。载荷P位于纵向对称面Oxy内，杆件承受单向偏心压缩，其简图为(b)。将P平移至轴线，如图(c)所示，杆件承受压弯组合变形。

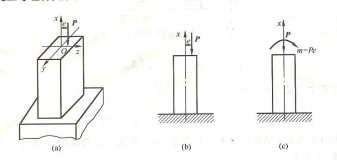
单向偏心压缩

各横截面的内力：F_N=P, M_y=Pe (y为中性轴)。易知各个横截面的右侧边缘有最大压应力：

若偏心距e较大，则弯曲最大应力大于压缩应力，横截面左侧边缘会出现拉应力：

对于脆性材料的受压立柱，由于材料抗拉能力较差以从强度方面考虑，希望横截面上的拉应力很小或不出现拉应力，这就要求偏心距控制在一定范围之内。

当外力不在纵向对称面时，称为双向偏心拉压。以图（a）所示矩形截面杆为例，载荷P位于Oyz面上K点，讨论任意横截面四个角点的应力。

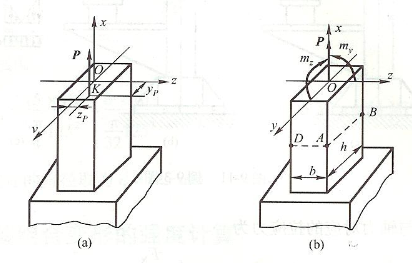
双向偏心拉伸

将力P平移至轴线，如图(b)所示，附加力偶矩为纵向对称面Oxy、Oxz内的两个力偶，力偶矩矢大小为m_z=Py_P，m_y=Pz_P。轴向力使杆件受拉，附加力偶使杆件在Oxy和Oxz面产生弯曲，中性轴分别为z、y轴，因此，杆件承受拉伸和双向弯曲的组合变形。

各横截面的内力：F_N=P，M_z=Py_P，M_y=Pz_P。可知各个横截面有相同的应力分布。利用叠加法，可求得横截面四个角点的应力。

结果若为负值，则表示应力为压应力。