-
1 内容
-
2 PPT
-
3 视频
强度理论概述
材料在单向应力状态下的强度(塑性材料的屈服极限,脆性材料的强度极限)总可通过拉伸试验和压缩试验加以测定;材料在纯剪切这种特定平面应力状态下的强度(剪切强度)可以通过例如圆筒的扭转试验来测定。
但是对于材料在一般二向应力状态下以及三向应力状态下的强度,则由于不等于零的主应力可以有多种多样的组合,所以不可能总是由试验加以测定。因而需要通过对材料破坏现象的观察和分析寻求材料强度破坏的规律,提出关于材料发生强度破坏的力学因素的假设——强度理论,以便利用单向拉伸试验测得的强度来推断复杂应力状态下材料的强度。
材料的强度破坏有两种类型,即在没有明显塑性变形情况下的脆性断裂和产生显著塑性变形而丧失工作能力的塑性屈服。工程中常用的强度理论按上述两种破坏类型分为:
(1)研究脆性断裂力学因素的第一类强度理论,其中包括最大拉应力理论和最大伸长线应变理论。
(2)研究塑性屈服力学因素的第二类强度理论,其中包括最大切应力理论和形状改变比能(形状改变能密度)理论。
最大拉应力理论(第一强度理论)
受铸铁等材料单向拉伸时断口为最大拉应力作用面等现象的启迪,第一强度理论认为,在任何应力状态下,当一点处三个主应力中的拉伸主应力达到该材料在单轴拉伸发生脆性断裂的极限应力时就发生断裂。因此,第一强度理论关于脆性断裂的判据为
而相应的强度条件则是
式中,[s]为对应于脆性断裂的许用拉应力
n为断裂安全系数。这一理论与均质脆性材料(例如铸铁、玻璃、石膏等)的实验结果相吻合。
最大拉应变理论(第二强度理论)
第二强度理论认为,在任何应力状态下,当一点处的最大伸长线应变ε1,达到该材料在单轴拉伸试验中发生脆性断裂时与断裂面垂直的极限伸长线应变eb时就会发生断裂。因此,第二强度理论关于脆性断裂的判据为
对于式中材料脆性断裂的极限伸长线应变eb,如是由单轴拉伸试验测定的(例如,对铸铁等脆性金属材料),那么eb=sb/E;故有断裂的判据为
由广义胡克定律
得断裂判据为
则相应的强度条件则为
式中,[s]为对应于脆性断裂的许用拉应力。石料或混凝土等脆性材料受轴向压缩时,往往出现纵向裂缝而断裂破坏,而最大伸长线应变发生于横向,最大伸长理论可以很好的解释这种现象。但是实验结果表明,这一理论仅仅与少数脆性材料在某些情况下的破坏相符,并不能用来解释脆性破坏的一般规律,故工程上应用较少。
最大切应力理论(第三强度理论)
低碳钢在单轴拉伸而屈服时出现滑移等现象,而滑移面又基本上是最大切应力的作用面(45°斜截面)。据此,第三强度理论认为,在任何应力状态下当一点处的最大切应力tmax达到该材料在试验中屈服时最大切应力的极限值ts时就发生屈服。第三强度理论的屈服判据为
对于由单轴拉伸试验,可测定屈服极限ss ,从而有ts=ss/2,上列屈服判据可写为
即
相应的强度条件则为
式中,[s]为对应于屈服失效的许用应力
n为屈服安全系数。从上述屈服判据和强度条件可见,这一强度理论没有考虑复杂应力状态下的中间主应力对材料发生屈服的影响,因此它与试验结果会有一定误差,但结果偏于安全。
形状改变比能理论(第四强度理论)
注意到三向等值压缩时材料不发生或很难发生屈服,第四强度理论认为,在任何应力状态下材料发生屈服是由于一点处的形状改变比能或形状改变能密度达到该材料在单向拉伸试验发生屈服失效时形状改变比能的极限值所致。
复杂应力状态的形状改变比能为
单向拉伸试验发生屈服失效时形状改变比能为
屈服判据为
相应的强度条件则为
这个理论比第三强度理论更符合已有的一些二向应力状态下的试验结果。
摩尔—库仑理论
前面所述四个强度理论,主要是采用科学假设的方法建立的,它们是对决定材料强度失效或破坏的主要因素,根据一定的实验基础,进行假设,然后验证。所以观点明确,物理意义清楚。当然,强度失效或破坏的因素很多(特别是微观、细观因素很多),一两个主要因素不可能概括全部,因此理论与实验之间的偏差是难免的。正是这种原因,以往有些强度理论尽管物理意义似乎很合理(例如最大伸长线应变理论),但由于同实验结果偏差太大,也很快被淘汰。因此,一个从宏观角度描述现象的理论能否成立,关键仍在于能否同实验结果相符合。所以基于这种考虑,近代工程科学中较多地采用唯象学的方法,即根据尽可能多的实验结果对现象和数据进行综合分析和描述,确定出其行为过程,而不过多地注意其物理意义的阐述。摩尔-库仑强度理论就是综合实验结果建立的。
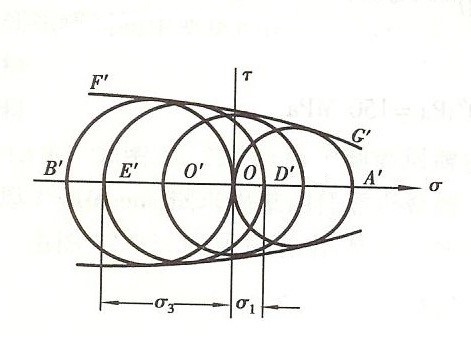
单向拉伸试验时,失效应力为屈服极限σs或强度极限σb。在σ-τ平面内,以失效应力为直径作应力圆OA′,称为极限应力圆。同样,在单向压缩试验确定的极限应力圆为 OB′。由纯剪切试验确定的极限应力圆是以OO′为半径的圆。对任意的应力状态,设想三个主应力按比例增加,直至材料以屈服或断裂的形式失效。这时,由三个主应力可确定三个主应力圆。现在只作出三个应力圆中最大的一个,亦即由σ1和σ3确定的应力圆,如图中的圆D′E′。按上述方式,在s-t面内得到一系列的极限应力圆。于是可以做出它们的包络线F′G′。包络线当然与材料的性质有关,不同的材料包络线也不一样;但对同一材料则认为它是唯一的。
对一个已知的应力状态σ1、σ2、σ3,如由σ1和σ3确定的应力圆在上述包络线之内,则这一应力状态不会引起失效。如恰与包络线相切,就表明这一应力状态已达到失效状态。
在实用中,为了利用有限的试验数据便可近似地确定包络线,常以单向拉伸和压缩的两个极限应力圆的公切线代替包络线,若再除以安全系数,便得如图所示以圆的公切线代替包络线的情况。
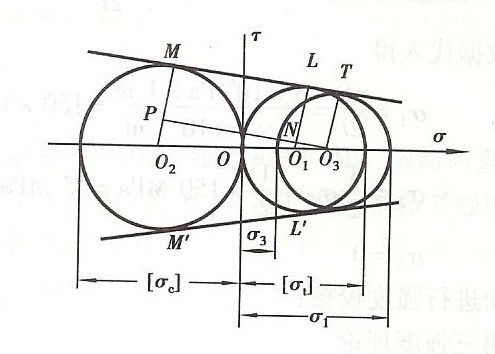
图中[σt]和[σc]分别为材料的抗拉和抗压许用应力。若由σ1和σ3确定的应力圆在公切线ML和M′L′之内,则这样的应力状态是安全的。当应力圆与公切线相切时,便是许可状态的最高界限。由图中各线段间的几何关系可得到
考虑到一定的安全储备,于是摩尔—库仑理论的强度条件为
对抗拉和抗压强度相等的材料,上式化为
成为第三强度理论的强度条件。
当σ3=0或σ1=0 时分别同单向拉伸或单向压缩实验吻合。
摩尔—库仑强度理论可以用来说明材料的脆性断裂和塑性屈服,但仍然未考虑σ2的影响。与前述四个强度理论相比较,它不是只考虑应力或应变各因素中的一个,而是考虑了它们的组合,因此摩尔—库仑强度理论是比较完善的。
强度理论的统一形式
把各种强度理论的强度条件写成统一形式
sr称为复杂应力状态的相当应力。
强度理论的适用范围及其应用
1. 适用范围
(1)一般脆性材料选用第一或第二强度理论;
(2)塑性材料选用第三或第四强度理论;
(3)在二向和三向等拉应力时,无论是塑性还是脆性都发生脆性破坏,故选用第一或第二强度理论;
(4)在二向和三向等压应力状态时,无论是塑性还是脆性材料都发生塑性破坏,故选用第三或第四强度理论。
2.强度理论的计算步骤
(1)外力分析:确定所需的外力值;
(2)内力分析:画内力图,确定可能的危险面;
(3)应力分析:画危面应力分布图,确定危险点并画出单元体,求主应力;
(4)强度分析:选择适当的强度理论,计算相当应力,然后进行强度计算。


