由斜截面上的应力公式可知，正应力和切应力都是a的函数，说明它们在之间存在着函数关系。下面来推导这一关系。首先，将正应力和切应力公式分别改写成如下形式

然后将以上两式各自平方后相加，于是得

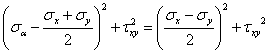
此式表示以正应力s_a和切应力t_a为变量的圆的方程。以s_a为横坐标，t_a为纵坐标，则此圆圆心O的坐标为；半径为

此圆称为应力圆或摩尔（Mohr）圆。圆上任一点的横纵坐标，则分别代表围绕一点的单元体在各个不同方位截面上的正应力与切应力。这种通过作应力圆求任意斜截面的应力的方法称为应力分析的图解法。

下面以图（a）所示平面应力状态为例，说明应力圆的做法。

图 (a)    

（1）作s-t坐标系；

（2）选择合适的比例尺，作出与截面x和y上两对应力所对应的点D（s_x，t_xy）和D′（s_y，t_yx）；

（3）连接D和D′两点，与s轴交于C点；

（4）以C点为圆心，CD为半径画圆，即为所要作的应力圆。

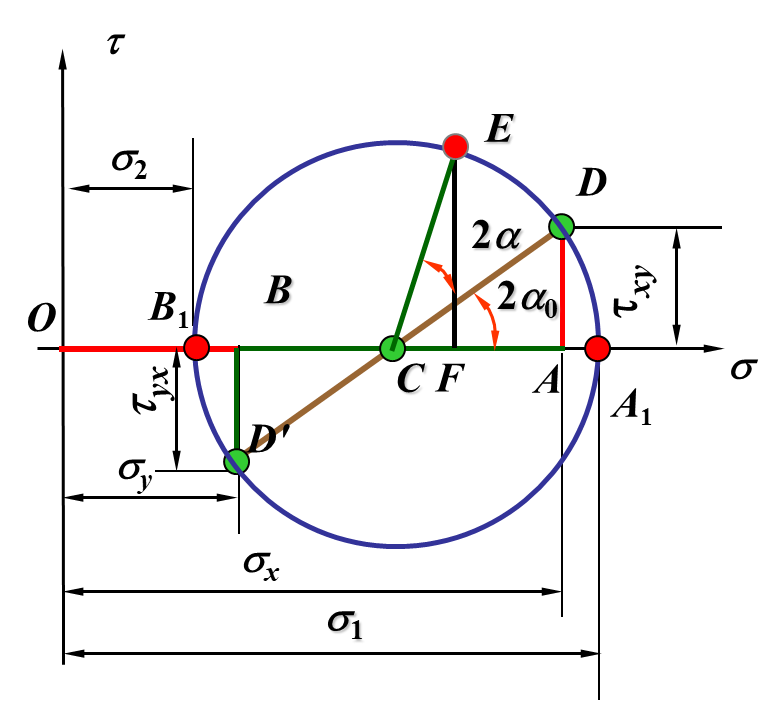
 图 (b)

要求图（a）中斜截面a上的应力，在应力圆上将线段CD沿a转向转过2a角，得E点。E点的横坐标和纵坐标值即分别为a斜截面上的正应力与切应力。

图（b）中的A₁、B₁两点的横坐标分别为

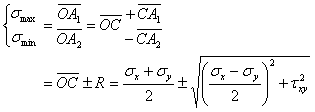
角Ð D C A₁为主应力所在面方位角的2倍。在应力圆中线段C D转向线段C A₁为顺时针，那么在图（a）的单元体上从x轴应顺时针转过a₀角，即为主平面。在图上A₁、B₁两点相差180°，则在单元体上两平面相差90°。

图（c）

图（c）中G₁和G ₂是最大切应力和最小切应力对应的点，其值等于R，两点相差180°，则在单元体上最大切应力和最小切应力所在的平面相差90°，线段G₁ G ₂与线段A₁B₁正交，说明在单元体上主平面与最大切应力和最小切应力所在平面相差45°。

综上所述，应力圆与单元体有如下对应关系：

• 点面对应。应力圆上某一点的坐标值，分别对应着单元体上某一方位面上的正应力与切应力。

• 转向对应。应力圆半径旋转时，单元体上斜截面的外法线绕x轴应沿相同转向旋转。

• 二倍角对应。应力圆上的角度是相应单元体上角度的2倍。

• 应力符号对应。单元体上正号正应力，在应力圆上位于纵坐标的右方，反之位于左方；使单元体有逆时针旋转趋势的切应力，在应力圆上位于横坐标轴的下方，反之位于上方。