工程上，一般构件的受力都比较复杂，因此，在构件的某一点处所取得已知单元体方向的应力通常不是最大的应力方向。下面来讨论平面应力状态下，已知通过一点的某些截面上的应力后，如何确定通过这一点的其他截面上的应力，从而确定主应力和主平面及其最大切应力。

从受力构件上截取一单元体abcd。其一对侧面上应力为零，而另两对侧面上分别作用有应力sx，sy，txy，tyx如图 (a)所示，这类单元体是平面应力状态的一般情况。图 (b)为单元体的正投影。

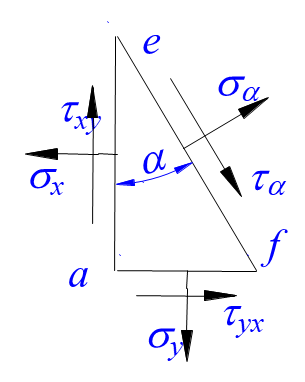
        （a）                                         （b）                                                      （c）

这里s_x，t_xy是法线与y轴平行的面上的正应力和切应力；s_y，t_yx是法线与x轴平行的面上的应力。切应力t_xy第一下角标x表示切应力作用平面的法线的方向，第二下角标y表示切应力的方向；应力的正负号规定为：正应力以拉应力为正，而压应力为负；切应力对单元体内任意点的矩为顺时针转向时为正，反之为负。按照以上规定，在图 (a)中，s_x、s_y、t_xy皆为正，而t_yx为负。假想取任一与xy平面垂直的斜截面ef，如图 (b)，其外法线n与y轴的夹角为a。规定由x轴逆时针转向外法线n时，a为正，反之为负。以截面ef把单元体截开，取左半部分aef为研究对象，如图 (c)。斜截面上的正应力为s_a，切应力为t_a。设ef面的面积为dA，则af面和ae面的面积分别是dAsina和dAcosa, 把作用于aef部分上的力投影于ef面的外法线n和切线t的方向，列静力平衡方程，得：

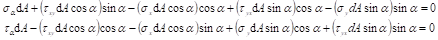
由切应力互等定理有t_xy=t_yx，代入以上平衡方程，整理得

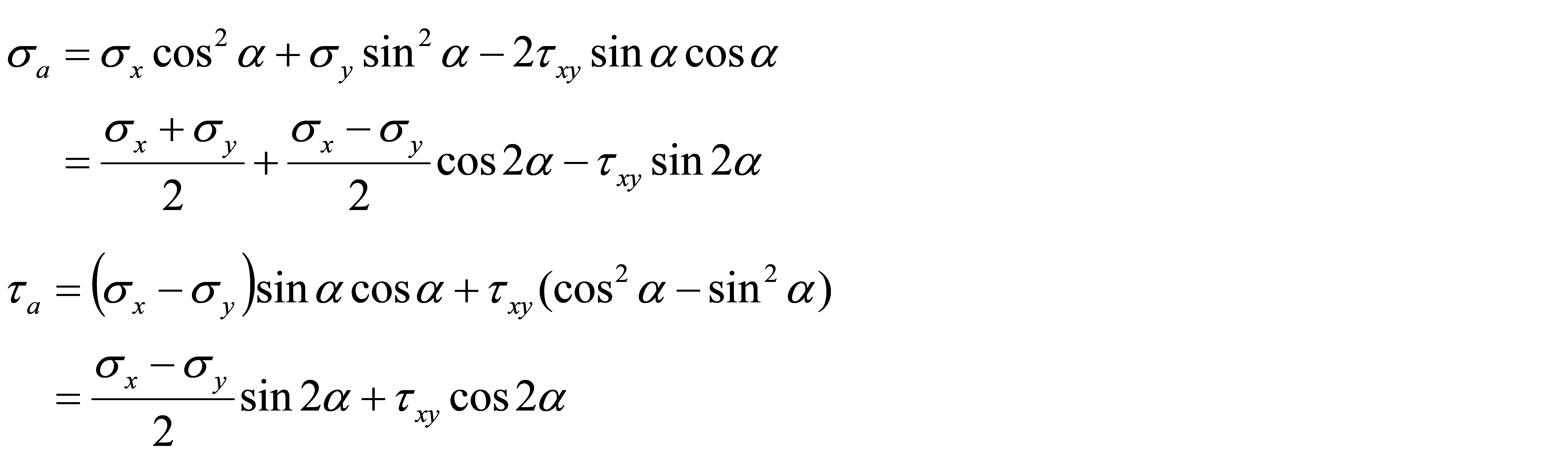
可见，斜截面上的正应力和切应力都是角a的函数。这样，在平面应力状态下，只要知道一对互相垂直面上的应力和a，就可以依上式求出a为任意值时的斜截而上的应力。

下面来推导主应力和确定主平面的角度的公式。

将斜截面上的正应力对a求导数并令此导数等于零，可求得正应力达到极值时的方位角，用a₀来表示。

由上式可求出a₀的相差90°的两个根，它们确定相互垂直的两个平面，其中一个是最大正应力所在平面，另一个是最小正应力所在的平面。

由三角关系

整理后可求得最大正应力和最小正应力的计算表达式

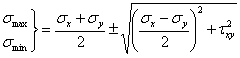
比较上式和斜截面上切应力的表达式可见，满足上式的角a₀恰好使t_a0等于零，这表明正应力取得极值的截面上，切应力必为零，即正应力的极值就是单元体的主应力。

用相似的方法，可以确定最大和最小切应力以及它们所在的平面。将斜截面上切应力的表达式对a求导数，得

令此导数等于零，可求得切应力取得极值时的a值，用a₁来表示，有

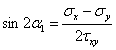
由此式也可求出相差90°的两个a₁，其中一个对应的作用面是切应力极大值所在的平面，另一个对应的作用面是切应力极小值所在的平面，两个切应力分别称为最大切应力和最小切应力。将上式结果代入切应力表达式，求得切应力的最大值和最小值为

比较a₀和a₁，有

所以有

即最大和最小切应力所在平面与主平面的夹角为45°。