应力状态的概念

构件在受力时将同时产生应力与应变。构件内的应力不仅与点的位置有关，而且与截面的方位有关，应力状态理论是研究指定点处的方位不同截面上的应力之间的关系。应变状态理论则研究指定点处的不同方向的应变之间的关系。应力状态理论是强度计算的基础，而应变状态理论是实验分析的基础。

研究表明，构件内不同位置的点，一般情况下具有不同的应力，所以点的应力是该点坐标的函数。然而就一点来论，不同方位截面上的应力也不同，截面上的应力又随截面方位的不同而变化，是截面方位角的函数。因此，所谓“一点的应力状态”就是指过一点各个方位截面上的应力情况的总体。

为了表示一点应力状态,一般是围绕该点取出一个三个方向尺寸均为无穷小的正六面体，简称为单元体。由于单元体是无限小的，因此可以认为单元体各面上应力是均匀的，单元体相互平行的截面上应力相同。

在物件内任一点总可以取出一个特殊的单元体，其3个相互垂直的面上都无切应力，这种切应力为零的截面称为主平面，主平面上的正应力称为主应力。这样特殊的单元体称为主单元体，主单元体上3个主应力按代数值大小排列为

当三个主应力均不为零时，称该点处于三向应力状态。若只有两对面上的主应力不等于零，则称为二向应力状态或平面应力状态。若只有一对面上的主应力不为零，则称为单向应力状态。

应力状态实例

单向应力状态

轴向拉伸或压缩时构件上任意一点。

横力弯曲时梁横截面上、下边缘点处。

平面应力状态

横力弯曲时梁横截面除上、下边缘点以外的各点。

薄壁压力容器

如果容器的壁厚t 远小于容器中面的最小曲率半径R（如t£R/20），则这种容器就称为薄壁容器；反之，称为厚壁容器。

圆筒形薄壁容器

设圆筒形薄壁容器的平均直径为D，壁厚为t，容器所装流体的压力为p，如图（a）所示，如果不考虑圆筒自重和圆筒内所装流体的重量，则筒体在内压力作用下只产生轴向伸长和周向胀大的变形，因此在筒壁的纵横两截面上只有正应力，而无剪应力。

用横截面将圆筒截开，取筒的左半边部分连同所装流体一起为隔离体（图（b）），由于筒壁很薄，可认为筒壁中的应力沿壁厚是均匀分布的。

流体作用于隔离体的压力的合力为

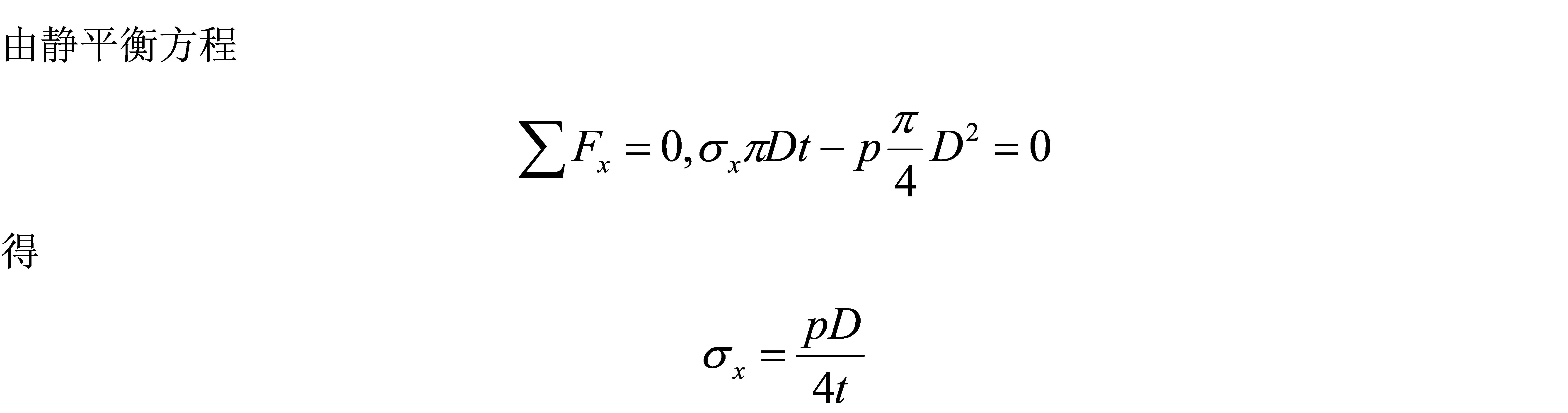
再用两个横截面在离端盖较远处截取长为l的圆筒，并以纵向对称面将其截为两半，取其下半部分连同所装液体一起为分离体（图（c）），同样认为应力沿壁厚是均匀分布的。流体作用于分离体的压力的合力为

即圆筒形薄壁容器的筒壁的周向应力为轴向应力的2倍。

圆筒壁上任一点A的应力状态如图（a）所示，要说明的是，圆筒内表面虽然直接受内压p的作用，但p远小于轴向应力和周向应力，于是由内压p引起的径向应力可以忽略不计；又圆筒外表面为自由表面，因此圆筒上任一点处的应力状态可近似地看作为二向应力状态。

圆球形薄壁容器

设圆球形薄壁容器的平均直径为D，壁厚为t。所受内压为p。如图（a）所示。

由于圆球的对称性，可取半个圆球连同所装的流体一起为分离体(图（b）)。流体作用于分离体的压力的合力为

由静平衡方程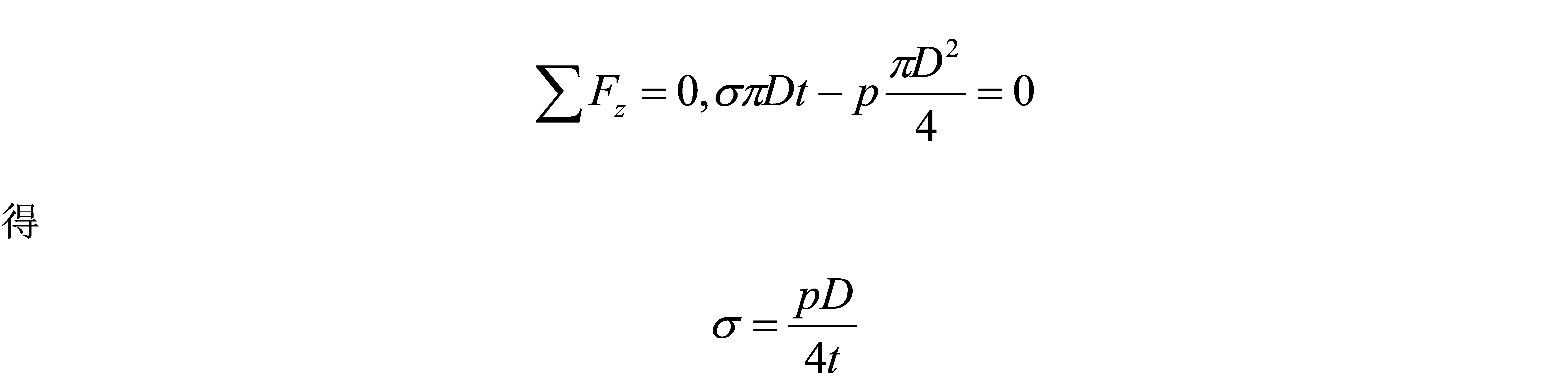得

如果略去径向应力，则球璧上任一点A处的应力状态如图（a）所示，为一等值二向应力状态。

三向应力状态

岩石的三轴压缩试验、钢轨的轨面受车轮的静荷作用时，其应力状态为三向压应力状态。

金属拉深成型过程中各点受力复杂，分别承受单向应力状态、平面应力状态和空间应力状态。