积分法虽然可以求得挠曲线方程和转角方程，可得到任意截面的转角和挠度，但是计算过程比较麻烦，工程中往往关心的某些特殊截面上的挠度和转角，特别是梁的最大挠度和转角，并不要求求出挠曲线或转角方程，常常采用叠加法。

在小变形、线弹性前提下（材料服从胡克定律），挠度与转角均与载荷成线性关系。因此，当梁上有多个载荷作用时，可以分别求出每一载荷单独引起的变形，把所得变形叠加即为这些载荷共同作用时的变形，这就是弯曲变形的叠加法。

为了便于工程计算，把简单基本载荷作用下梁的最大挠度，最大转角计算公式列出以便查用。

基本梁的挠度和转角（抗弯刚度为EI，跨度为l，C为中点）

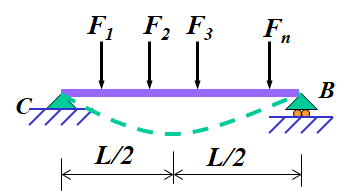
一、载荷叠加（直接叠加法）

多个载荷同时作用于结构而引起的位移等于每个载荷单独作用于结构而引起的位移的代数和。

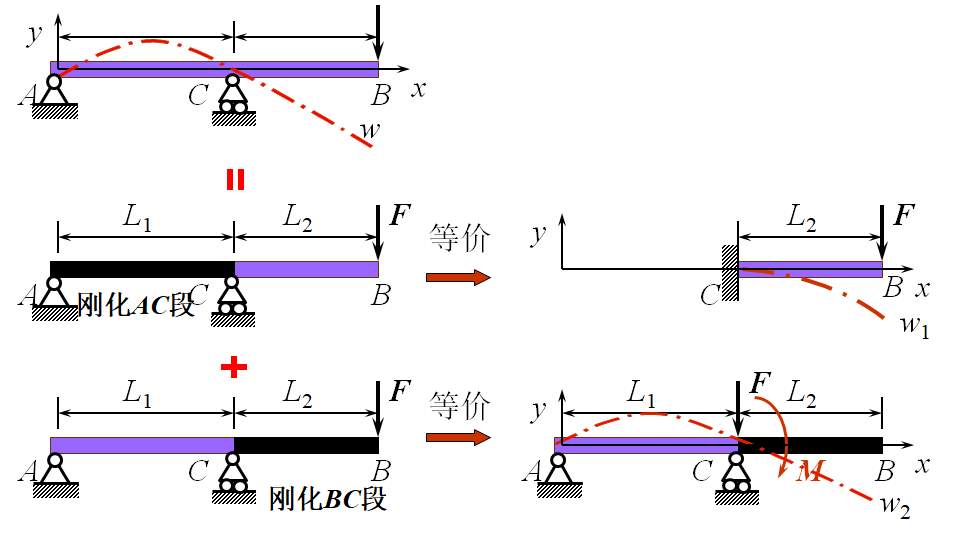
二、结构形式叠加（逐段刚化法）

为求图示外伸梁B截面的挠度，将梁的BC段视为C端为固定端的悬臂梁，此梁在F作用下B截面的挠度为w1。外伸梁的C截面并非固定不动，而要产生转角，截面的转动对BC段位移的影响，相当于使BC段绕C点刚性转动，此时B截面的竖向位移为w2。将w1与w2叠加就是外伸梁B截面的挠度，即

讨论：

叠加法求位移虽然比较简便、快速，但具体运用时，往往需经过分析、处理及运用等效力系后，才能利用表中的公式，比较灵活。

叠加法中的叠加是代数相加，在求若干荷载共同作用下的转角和挠度时，应注意每项的正、负。

上表中所列六个公式需要强记。