基本概念

以简支梁为例，以变形前的轴线为x轴，垂直向上为y轴，xoy平面为梁的纵向对称面。 

①挠曲线：

在对称弯曲情况下，变形后梁的轴线为xoy平面内的一条光滑连续的平面曲线，此曲线称为挠曲线。

②挠度：

梁的任一截面形心的竖直位移称为挠度。

③挠曲线方程：w=f(x)

④转角：弯曲变形中，梁的横截面对其原来位置转过的角度θ，称为截面转角。

根据平面假设，梁的横截面变形前，垂直于轴线，变形后垂直于挠曲线。故转角为挠曲线的法线与y轴的夹角，也等于挠曲线的切线与x轴的夹角。挠度与转角的关系为

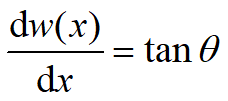
小变形情况下

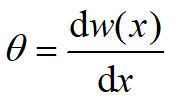
⑤挠度w和转角θ是度量弯曲变形的两个基本量。

⑥挠度与转角符号规定：在图示坐标中，挠度向上为正，反时针的转角为正。

梁的挠曲线近似微分方程

对于图示简支梁，考虑dx 微段的变形。

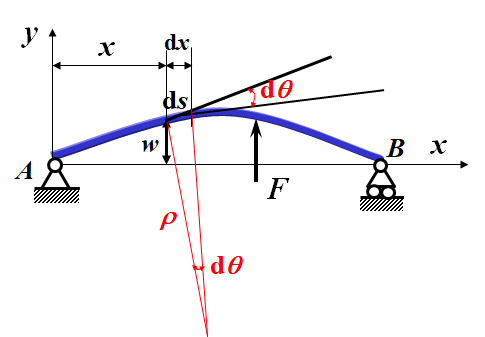
根据平面弯曲梁变形的基本公式

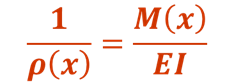
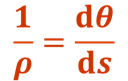
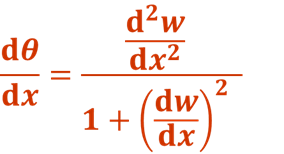
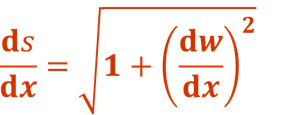
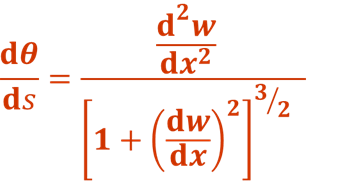
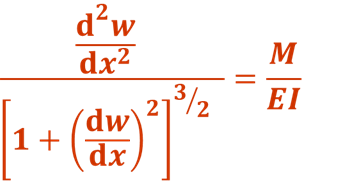
此式即为挠曲线的微分方程，适用于弯曲变形的任意情况，它是非线性的。在小变形的情况下，梁的挠度w一般都远小于跨度，挠曲线w=f(x)是一非常平坦的曲线，转角θ也是一个非常小的角度，于是

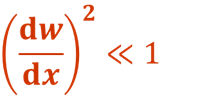
故可得

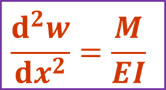
此式为挠曲线的近似微分方程。

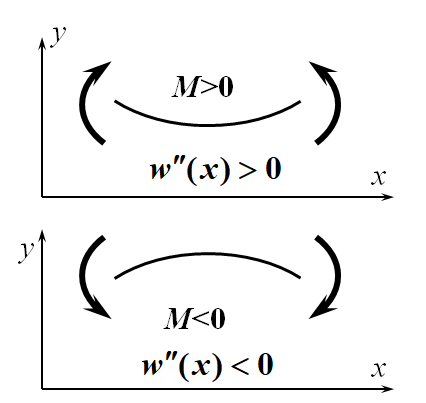
在图示坐标系内，若弯矩M为正，则挠曲线向下凸，有极小值，挠度的二阶导数亦为正值。若弯矩M为负，则挠曲线向上凸，有极大值，挠度的二阶导数亦为负值。