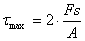切应力的分布规律与梁的横截面形状有关，因此以梁的横截面形状不同分别加以讨论。

 1．矩形截面梁

（1）切应力的分布规律

两点假设:

   切应力与剪力平行；

   距中性轴等距离处，切应力相等。

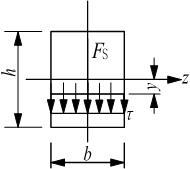
当h>b时，按上述假设得到的解答与精确解相比有足够的准确度。

（2）切应力沿截面高度的变化规律

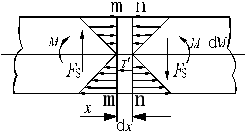
①从梁中取出dx段，而微段上无载荷作用。

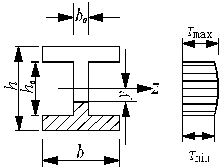
②截面上的σ和τ的分布如图。

③研究微块的平衡

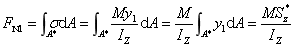
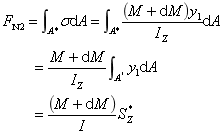
式中：为离中性轴为y的横线以下面积对中性轴之静矩。

考虑到微块顶面上相切的内力系的合力 

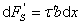
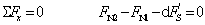
由切应力互等定理，横截面上pq线处切应力为

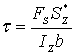
这就是矩形截面梁弯曲切应力计算公式。

④讨论：

a. 横力弯曲下梁的纵向纤维层之间存在切应力。

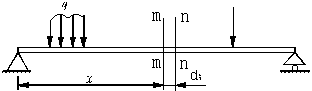
b. 矩形截面切应力沿高度的变化规律如图。

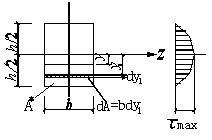
说明切应力τ沿截面高度按抛物线规律变化。

c. 最大切应力发生中性轴上。 

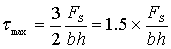
2．工字形截面梁

（1）计算表明：截面上剪力F_S的95～97%由腹板承担，故只考虑腹板上的切应力分布规律，而腹板是一个狭长矩形，矩形截面切应力两个假设均适用（τ方向与F_S一致，设宽度均布），采用矩形截面方法可得：

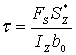
式中：

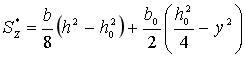
以y=0，代入上式得 

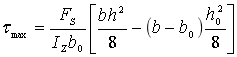
∵b₀<<b

∴τ_max≈τ_min

于是近似认为

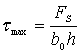
（2）翼缘中切应力分布比较复杂，且数量很小，无实际意义，不予讨论。

（3）工字梁翼缘的全部面都距中性轴较远，每一点的正应力都很大，所以工字梁的最大特点是，用翼缘承担大部分弯矩，腹板承担大部分剪力。

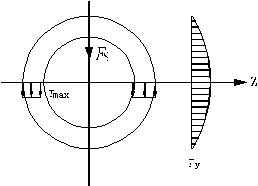
3．圆形及圆环形截面梁

 （1）圆形截面

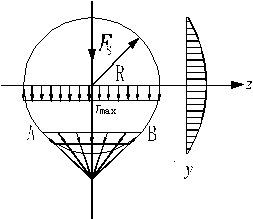
 在中性轴上

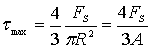
（2）圆环形截面