一、纯弯曲时的正应力

图示梁中间段只有弯矩没有剪力，称为纯弯曲。两端即有剪力以有弯矩称为横力弯曲（剪切弯曲）。

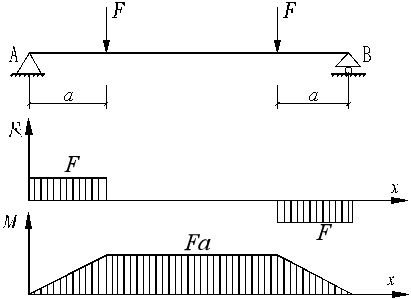
变形观察：

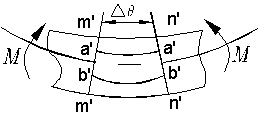
变形前的直线aa、bb变形后成为曲线a'a'、b'b'，变形前的直线mm、nn变形后仍为直线m'm'、n'n'，然而却相对转过了一个角度，且仍与a'a'、b'b'曲线相垂直。

假设

（1）平截面假设

变形前为平面的横截面变形后仍为平面，且仍垂直于变形后梁的轴线。

（2）纵向纤维互不挤压假设

设想梁是由平行于轴线的众多纤维组成。在纯弯曲过程中各纤维之间互不挤压，只发生伸长和缩短变形。

中性层与中性轴

显然，凸边一侧的纤维发生伸长，凹边一侧的纤维缩短。由平截面假设和连续性假设，纤维由伸长变为缩短，连续变化，中间一定有一层纤维称既不伸长,也不缩短,这一层纤维为中性层。中性层与横截面的交线称为中性轴，由于整体变形的对称性，中性轴由与纵向对称面垂直。可以证明，中性轴为形心主轴。

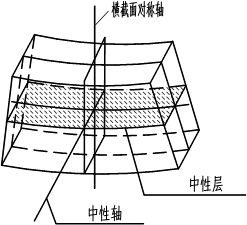
正应力分布规律

（1）变形几何关系

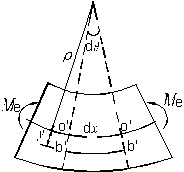
取dx微段来研究，竖直对称轴为y轴，中性轴为z轴，距中性层为y的任一纤维bb的线应变。

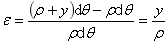
（2）物理关系

因为纵向纤维之间无正应力，每一纤维都是单向拉伸或者单向压缩，当应力小于比例极限时，由胡克定律

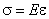
得：

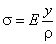
此式表明：任意纵向纤维的正应力与它到中性层的距离成正比。在横截面上，任意点的正应力与该点到中性轴的距离成正比。亦即沿截面高度，正应力按直线规律变化。

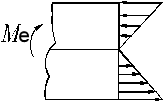
（3）静力关系

横截面上的微内力σdA组成垂直于横截面的空间平行力学。这一力系可能简化为三个内力分量：

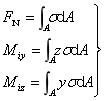
横截面上的内力与截面左侧的外力必须平衡。在纯弯曲情况下，截面左侧的外力只有对z轴的力偶矩Me。由于内外力必须满足平衡方程，故：

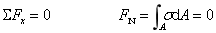
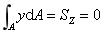
结论：z轴（中性轴）通过形心。

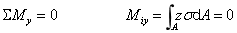
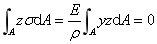
结论：y轴为对称轴，上式自然满足。

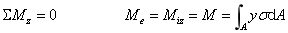
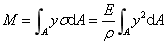
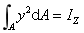
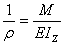
式中1/ρ为梁轴线变形后的曲率，称为梁的抗弯刚度。

由曲率公式代入物理关系中得：

此式即为纯弯曲时梁的正应力计算公式。

讨论：

（1）导出公式时用了矩形截面，但未涉及任何矩形的几何特性，因此，公式具有普遍性。

（2）只要梁有一纵向对称面，且载荷作用于对称面内，公式都适用。

（3）横截上任一点处的应力是拉应力还是压应力可直接判定，不需用y坐标的正负来判定。

二、横力弯曲（剪切弯曲）时的正应力

纯弯曲正应力公式可推广应用于横力弯曲

讨论：公式的适用条件

（1）平面弯曲

（2）纯弯曲或l/h≥5的横力弯曲（σ，τ）

（3）应力小于比例极限。

最大正应力

引入记号：

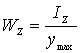
Wz——抗弯截面系数（m³）

讨论：

（1） 等直梁而言σ_max发生在最大弯矩断面，距中性轴最远处y_max。

（2）对于变截面梁不应只注意最大弯矩M_max截面，而应综合考虑弯矩和抗弯截面系数W_z两个因素。