一、  剪力、弯矩与分布荷载间的关系

图示简支梁受分布载荷作用，假设分布载荷向上为正，下面分折分布载荷集度与剪力和弯矩的微分关系。为了研究的一般性，在x截面处截取微段dx为研究对象，画出微段左侧和右侧的剪力和弯矩。

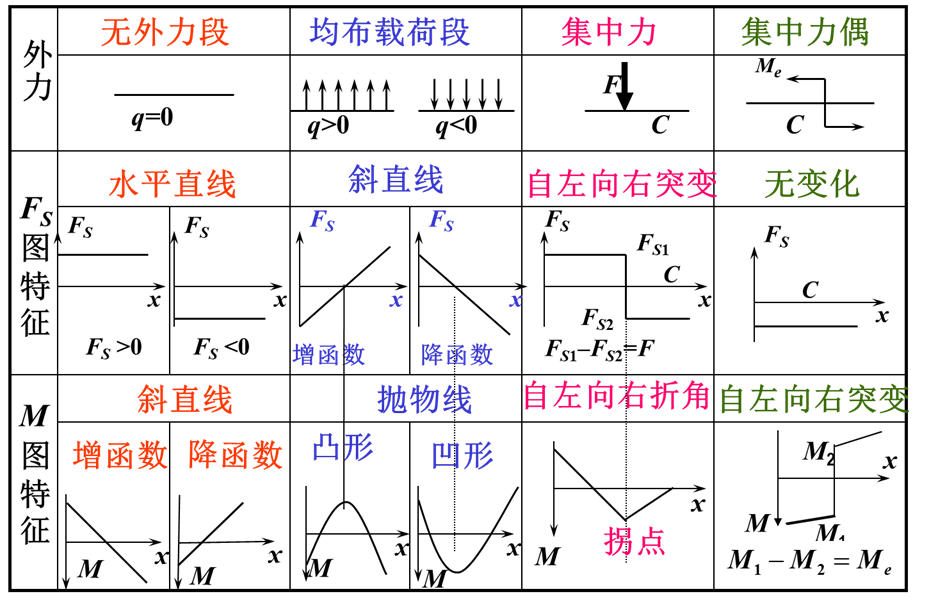
当q=0时，剪力为常数，剪力图为水平直线；

当q=常数>0时，剪力图为斜直线，且斜率为正；

当q=常数<0时，剪力图为斜直线，且斜率为负。

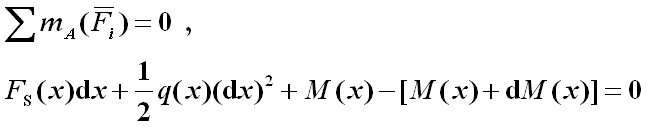
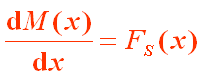
上式表明：弯矩图上某点处的切线斜率等于该点处剪力的大小。

当剪力为零时，弯矩图为水平线；当剪力为正常数时，弯矩图为斜率为正的斜直线；当剪力为负常数时，弯矩图为斜率为负的斜直线。当剪力图为斜直线时，弯矩图为二次抛物线。

弯矩与荷载集度的关系是：

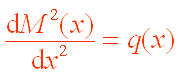
当q为正值时，弯矩对x的二阶导数大于零，表明弯矩图为有极小值的抛物线，当弯矩坐标向下为正是为凸形抛物线，抛物线的极值点对应一阶导数等于零，即剪力等于零；q为负值时，弯矩图为凹形抛物线；当q=0时，弯矩图为斜直线。

二、剪力、弯矩与外力间的关系

根据分布载荷集度与剪力和弯矩的微分关系及简单梁的内力图特点，将各种受力情况下剪力和弯矩图变化规律列成下表，可在作内力图时应用。

三、简易作图法

利用内力和外力的关系及特殊点的内力值来作内力图的方法称为简易作图法，作图步骤如下框图。

首先根据静力学平衡方程求约束反力；根据梁上载荷作用情况和支座情况进行分段，利用内力和外力的关系判断每一段剪力图和弯矩图的大致形状；然后从梁的左端开始向右作图，作剪力图时，遇到向上的集中力，剪力图向上突变，突变的大小等于集中力的数值。遇到向下的集中力，剪力图向下突变。作弯矩图时，遇到顺时钟的集中力偶时，弯矩图向下（弯矩图的正方向）突变。画二次曲线时除了确定起止点的坐标外，还需要确定极值点的坐标，当剪力为零时弯矩有极值。

如何合理利用外力与内力的关系作剪力图和弯矩图是本章乃至材料力学这门课程的重点。不仅要能准确、迅速地根据载荷作用情况作出剪力图和弯矩图，而且还应能根据已知的剪力图作出载荷图和弯矩图或已知弯矩图作出载荷图和剪力图；不仅会作单跨梁（简支梁、悬臂梁、外伸梁）的剪力图和弯矩图，而且会作简单双跨梁的剪力图和弯矩图。