实验原理         

    

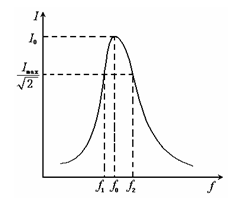
              图8-1                                   图8-2

图8-1所示电路为RLC串联电路。若取电阻R的端电压u2为输出电压，则该电路的转移电压比为

          

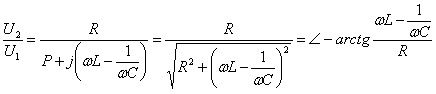
由上式可知，输出和输入电压的幅度比是角频率ω的函数，当频率很高时和频率很低时，幅度比都将趋于零，而在某一频率ω₀时，ω₀L=1/ω₀C，振幅比等于1，为最大值。我们把具有这种性质的函数称为带通函数，该网络称为二阶带通网络。

二阶带通函数输出电压和输入电压的振幅比是频率函数，其特性曲线如图8-2所示，称为该网络的幅频特性曲线。出现尖峰的频率ω0称为中心频率或谐振频率。这时，电路中的电抗部分为零，阻抗的模最小，称为纯电阻电路，电路中电流最大且与输入电压相同。我们把电路的这种工作状态叫做谐振。由此可见电路的谐振条件是：

即：            

改变角频率ω时，振幅比随之变化，当振幅比下降到峰值的0.707倍时的两个频率ω₁、ω₂分别叫做下3分贝频率和上3分贝频率。这两个频率的差值定义为该网络的通频率BW理论推导证明同频率BW=ω2-ω1=R/L，由电路的参数决定。

RLC串联电路的幅频特性的限度，可以用品质因数Q来衡量；Q的定义为：          

                                     

可见品质因数Q是由电路的参数决定的。当LC一定时，电阻R越小，Q值越大，通频带也越窄；反之，电阻R越大，品质因数Q越小，通频带BW也越宽，如图8-2所示。

     其次，当电路谐振时，X_L=X_C,电路为纯电阻性的，电流最大Im=U1m/R,因此，电容及电感上的电压的幅值分别为：

                                  

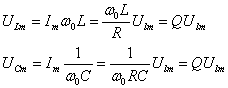
其幅值为输入电压的幅值的Q倍。若ω₀L=1/ω₀C远远大于电阻R，则品质因数Q远远大于1。在这种情况下，电容及电感上的电压就会远远超过输入电压。这种现象在无线电通讯中获得了广泛的运用，而在电力系统中，这种现象应极力设法避免。