实验原理

线性时不变渐进稳定电路在正弦信号激励下的响应，可以通过该电路的分方程式来求得，其解是由对应的齐次方程的解和非齐次方程的特解组成特解即是该电路的稳态解，其形式和激励一样也是正弦量。运用向量法电路的稳态响应，可以不必列出电路的微分方程，只需列出向量的代数程便可求出电路的稳态响应，从而使电路的计算大为简化。         

                                 

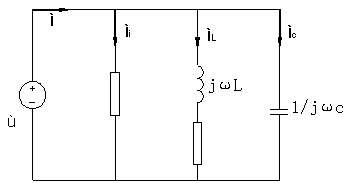
                        图6-1

1、R、L、C元件的向量关系

   报R元件来说，在正弦交流电路中的伏安关系和直流电路并没什么区别，其向量关系为

                                U=IR                            （6-1）

其中U=Um∠φu,I=Im∠φi Zc=1/jωc 将上式代入（6-1）式中

                                                                    （6-2）

由 (6-2）式可知电阻元件两端电压幅值和电流幅值符合欧姆定律，电流和电压是相同的。电阻值和频率无关。

电容C元件的相量关系为

                             U=Z_cI                             （6-3）   

其中电压相量U=UM ∠φu,电流相量I=Im∠φi，Zc=1/jωc ，将上式代入 (6-3）式得：        

                                          （6-4）

式(6-4）表示电容器C端电压的幅值及电流幅值不仅和电容U的大小有关，而且和角频率的大小有关。当电容C一定时，w越高，电容器的阻抗越小，在电压一定的情况下电流的幅值大；反之，频率越低电容器的阻抗越大，流过电容的电流越小。同时，公式表明流过电容的电流超前其端电压90。

 电感L元件的相量关系为

              U=IZ_l                 （6-5）

其中U=U_M ∠φu，I=Im∠φi，Z_L=jωl。将上式代入（6-5）式中得

                                                                 （6-6） 

式（6-6）表示电感L的阻抗是频率的函数，频率越高，电感的阻抗越大，在电压一定的情况下，流过电感的电流越小；反之，频率越低，感抗越小，流过电感的电流越大。电感中的电流落后其端电压90。

2、RLC并联电路中总电流和分电流的关系

图6-1为RLC并联电路，其中r为电感的绕线电阻。根据基尔霍夫电流定律:

            I=I_R+I_L+I_C                                              (6-7)

  其中         I_R=U/R       

                

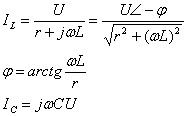
所以         

                                                       (6-8)

式(6-8)说明总电流相量I是各之路电流I_R 、I_L、 I_C 相量的代数和。