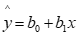线性回归模型是通过对历史数据进行训练获得一个线性模型以尽可能准确地预测实值X对应的Y值。在这个模型中，因变量Y是连续的，自变量X可以是连续或离散的。

在回归分析中，如果只包括一个自变量和一个因变量，且二者关系可用一条直线近似表示，称为一元线性回归分析；如果回归分析中包括两个或两个以上的自变量，且因变量和自变量是线性关系，则称为多元线性回归分析。对于二维空间线性是一条直线，对于三维空间线性是一个平面，对于多维空间线性是一个超平面。

一元线性回归分析预测法，是根据自变量x和因变量y的相关关系，建立x与y的线性回归方程进行预测的方法。由于市场现象一般是受多种因素的影响，而并不是仅仅受一个因素的影响。所以应用一元线性回归分析预测法，必须对影响市场现象的多种因素做全面分析。只有当诸多的影响因素中，确实存在一个对因变量影响作用明显高于其他因素的变量，才能将它作为自变量，应用一元相关回归分析市场预测法进行预测。

一元线性回归分析的特点如下：

（1）回归分析中，两个变量之间的关系是不对等的，因此必须根据研究目的，具体确定自变量与因变量。

（2）回归分析中的两个变量，自变量是给定的确定性变量，因变量是随机变量。

（3）在两个变量互为因果关系的情况下，可以有两个回归方程：y依x变化的回归方程和x依y变化的回归方程。但是不同方程所说明的问题是不一样的。

一元线性回归分析法的预测模型为：

式中：β₀、β₁是待估参数；u_i 是随机误差，是服从正态分布N(0,σ²)的随机变量，且独立。

线性回归方程为：