-
1 教学内容
-
2 练习
-
3 案例
-
4 扩展学习
第三节 离散程度的描述
某医学院用自编生存质量量表测得三组同年龄、同性别中年知识分子的躯体功能维度得分,资料如下:
甲组 8 8 9 10 11 12 12
乙组 5 6 8 10 12 14 15
丙组 1 2 5 10 15 18 19
均数=中位数=10(分),离散程度?
描述离散程度的常用指标:
极差? 四分位数间距? 方差? 标准差? 变异系数
(一) 极差 / 全距, R
极差大,说明变异程度大;极差小,说明变异程度小。
甲组 R=12-8= 4(分)
乙组 R=15-5=10(分)
丙组 R=19-1=18(分)
极差一般常用于:描述单峰对称分布小样本资 料的离散程度;初步了解资料的变异程度;当样本含量相差较大时,不宜用极差来比较资料的离散程度。
(二) 四分位数间距
1.百分位数(percentile, Px) : 位置指标,将观察值从小到大排列后处于第x百分位置上的数值。全部数据中,有x%的数据小于Px,有(100-x)%的数据大于Px 。
P50= M
百分位数的计算方法:
(1)直接法
当nx%=INT(nx%)时,PX=? ![]()
当nx% >INT(nx%)时,PX= ![]()
INT(nx%):n与x%乘积的整数部分。
根据下列资料求某市102名高中男生引体向上次数的第80%位数P80(数据已排序)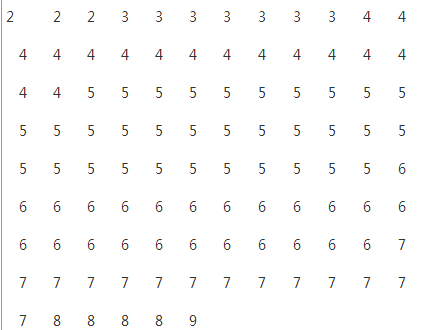
n=102, 102X80%=81.6, nx%> INT(nx%), ![]()
(2)频数表法: ![]()
例2.12? 用表2.4(见下)的资料求219名乳腺癌患者术后康复期生存质量评分的P25和P75。 ![]()
![]()
表2.4 219名乳腺癌患者康复期生存质量评分
评分 | 频数 | 累计频数 | 累计频率(%) |
0- | 2 | 2 | 0.91 |
30- | 2 | 4 | 1.83 |
40- | 3 | 7 | 3.20 |
50- | 11 | 18 | 8.22 |
60- | 30 | 48 | 21.92 |
70- | 63 | 111 | 50.68 |
80- | 60 | 171 | 8.08 |
90-100 | 48 | 219 | 100.00 |
2.四分位数间距 (inter-quartile range)
四分位数(quartile,简记为Q):
下四分位数 P25,QL;
上四分位数 P75,QU。
四分位数间距= QU-QL
例2.13 求219名乳腺癌患者术后康复期生存质量评分的四分位数间距。
四分位数间距=QU-QL=88.88-71.07=17.81(分)
四分位数间距数值越大,说明观察值分布的离散程度越大。
常用于描述偏态分布资料、两端无确切值或分布不明确资料的离散程度。
二、方差与标准差
单峰对称分布资料
(一) 方差(variance)? ![]()

(n-l) 自由度(degree of freedom)
例2.14用例2.2的资料计算某市120名9岁男孩肺活量的样本方差,已知![]() ,
, ![]()
![]()
(二) 标准差 (standard deviation)
方差的单位是平方,为还原单位,将方差开平方得到标准差。
1.直接法: 

例2.15 用例2.2资料计算某市120名9岁男孩肺活量的样本标准差。 

2.加权法:用于频数表资料。 
标准差是描述单峰对称分布资料离散程度最常用的指标。
标准差大,表示观察值之间变异程度大,即一组观察值的分布较分散;
标准差小,表示观察值之间变异程度小,即一组观察值的分布较集中。
对于经对数变换后呈正态分布或近似正态分布的资料,应将原始观察值取对数值后计算几何标准差。
三、变异系数(coefficient of variation)
用于:比较均数相差很大或计量单位不同的几组资料的离散程度。 ![]()
例2.17 某年某市城区120名5岁女孩身高均数为110.10cm,标准差为5.90cm;体重均数为17.71kg,标准差为1.44 kg,比较身高与体重的离散程度。
身高 
体重
可见,该市城区5岁女孩体重的变异大于身高的变异。


