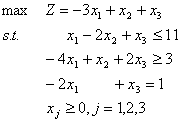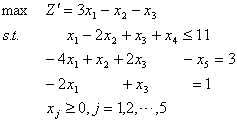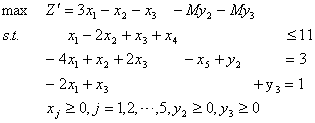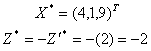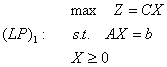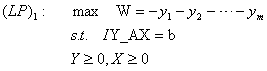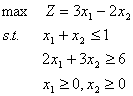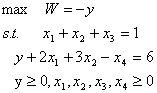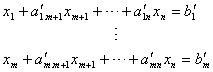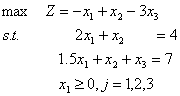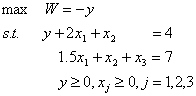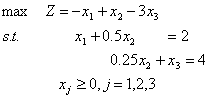引入人工变量——大M法和两阶段法

我们已经注意到，只有当存在初始的标准基时，才能使单纯形法来求解线性规划问题。如果欲求解的线性规划不存在标准基，就应当想办法变换出一个标准基。不过要注意的是，在变换的过程中，

    第一，应保持约束方程组的解集不变，即原问题的可行域不变，也就是说应当进行同解变换。

    第二，在获得标准基的同时，应使约束方程组右边的资源向量保持非负，这样才能使用单纯形法求解。

   一般来说，第一点要求是容易办到的，例如利用线性代数中关于行的初等变换就可以办到。然而，要同时做到这两点要求，常规的方法往往顾此失彼，很难满足要求。因此，应研究有效的办法来解决这个问题。下面介绍两种常见的方法。

一、大M法

大M法的基本思想是，如果将原问题标准化后的约束方程中仍无标准基，则可以在约束方程中添加人工变量，使之构成含有标准基的新问题，然后就可以用单纯形法求解新问题。显然，在新问题的某个解中，如果人工变量对应的分量是正数，则该解必不是原问题的可行解。因此，欲从新问题的解得到原问题的解，必须使新问题的可行解中的人工变量为零，而要达到这一点只须使人工变量全部成为非基变量即可。为达此目的，对极大化问题，可在原目标函数中加入绝对值充分大的负系数人工变量。这样，当对新问题用单纯形法求解时，在新目标函数的值逐步增大的迭代过程中，人工变量就会逐步退出基。

设原问题为

                                   （1-17）

引入人工变量

可得含有标准基的大M法新问题：

                （1-18）

其中，M是充分大的正数，I是m阶单位矩阵。

下面讨论新旧问题之间的关系。

首先要指出，新问题必有可行解，例如

就是新问题的一个可行解。于是，对新问题求解，其结果有两种可能：

1．新问题无最优解

此时可断言原问题无最优解。这是因为，此种条件下，意味着新问题存在可行点列（X_k，Y_k），使得

且                  

注意到M为充分大正数，故上式表明必有

即X_k是原问题的可行点列，且其对应的目标函数值有

表明原问题没有最优解。

2．新问题有最优解

设为则有：

（1）若是原问题的一个可行解。现任取原问题的一个可行解X，显然（X，0）是新问题的可行解，且其对应的目标函数值为于是有

表明，是原问题的最优解。

（2）若存在某个，则原问题没有可行解。因为此时新问题的最优值为

由，M为充分大的正数，上式显然是不可能的。所以，原问题没有可行解。

例1.8  用大M法求解线性规划

解  原问题标准化为

引入两个人工变量，原问题化为大M法问题：

此时，已拥有一个标准基，可用单纯形法求解，其计算过程及结果见表1-12。

在表1-12中，人工变量全部出基，故原问题的最优解及最优值为

表1-12

cj	3	-1	-1	0	0	-M	-M
初 始 表 1	x1	x2	x3	x4	x5	y2	y3
	1	-2	1	1	0	0	0	11
	-4	1	2	0	-1	1	0	3
	-2	0	（1）	0	0	0	1	1
	-6M+3	M-1	3M-1	0	-M	0	0	4M
迭代表 2	3	-2	0	1	0	0	-1	10
	0	（1）	0	0	-1	1	-2	1
	-2	0	1	0	0	0	1	0
	1	M-1	0	0	-M	0	1-3M	M+1
迭代表 3	（3）	0	0	1	-2	2	-5	12
	0	1	0	0	-1	1	-2	1
	-2	0	1	0	0	0	1	1
	1	0	0	0	-1	1-M	-M-1	2
最优表	1	0	0	1/3	-2/3	2/3	-5/3	4
	0	1	0	0	-1	1	-2	1
	0	0	1	2/3	-4/3	4/3	-7/3	9
	0	0	0	-1/3	-1/3	1/3-M	2/3-M	-2

二、两阶段单纯形法

两阶段单纯形法也是一种人工变量法，它的算法可分为两个阶段：

第一阶段，引入人工变量，构造一个具有标准基的新线性规划，求解这个新线性规划，其结果将有两种可能：或者将原问题的约束方程组化成具有标准基的形式，或者提供信息，表明原问题有可行解。

第二阶段，利用第一阶段所得的标准基，对原问题求解。

1．人工变量的引入

设原问题为

引入人工变量，构造新规划

其中，。

易知，新规划（LP）₁，具有以下3个特点：

（1）（LP）₁存在可行解，例如取Y=b，X=0，就得到一个可行解。

（2）（LP）₁必有最优解。这是因为，由于（LP）₁有可行解，且y_i非负，故（LP）₁的最大值上有界，不会超过零。

（3）（LP）₁存在一个标准基。

基于以上几点，可以用单纯形法求解（LP）₁，设其最优单纯形法为表1-13。

表1-13中，的系数。

显然，所有的检验数是最优值，故必有

若，则可断言原问题（LP）₁没有可行解。如果（LP）₁有行解，则有

那么，则是（LP）₁的一个可行解，且对应的目标值为

这与是最优值相矛盾。

表1-13

				b

例1.9  求解

解  将原问题标准化，再引入人工变量y，构造新规划：

其求解过程及结果见表1-14。

从表1-14可以看出，，表明原问题无可行解。事实上，容易验证，当均非负时，原问题的两个不等式约束是互不相容的。

若注意目标函数的表达式，可知必有全为零，可分两种情形讨论：

（1）人工变量全部是非基变量。不失一般性，可设是基变量，则表1-13等价于如下方程组：

 

对线性规划的可行域而言，单纯形法实质上是进行同解变换。因而上述方程组与原问题（LP）₁的约束方程组的解集相同，且由于已有一个标准基，故可用它取代原问题（LP）₁的约束方程组，再利用第四节中的单纯形法求解。

（2）某个人工变量y_s还是基变量。这时，显然有

表1-13中第s行等价于如下方程：

                  （1-19）

对（1-19）式可分两种情形进行讨论：

1）（1-19）式中所有的均为零。注意到所有的都为零。（1-19）式实际上是恒等式

0=0

说明表1-13的第s行是多余的、无意义的，应从表1-13中删除掉，约束方程减为m-1个，最优表中出现一个m-1阶的单位矩阵，正好可作为初始标准基。

2）（1-19）式中的不全为零，例如某个非零。此式，可用为主元，进行换基迭代，变量入基，而人工变量出基。由于有

此时将产生一个退化的基可行解。

表1-14

cj	-1	0	0	0	0
初 始 表	y	x1	x2	x3	x4
	0	1	（1）	1	0	1
	1	2	3	0	-1	6
	0	2	3	0	-1	6
	0	1	1	1	0	1
	1	-1	0	-3	-1	3
	0	-1	0	-3	-1	3

2．两阶段单纯形法的步骤

（1）第一阶段：首先将原问题标准化，得到（LP）₁形式，再引入必要的人工变量，构造新的线性规划（LP）₁，并用单纯形法解新规划（LP）₁，得到形如表（1-13）的最优单纯形表。若该表中的，则表明原问题没有可行解，应停止计算；若，表明已将原问题的约束方程组变换成了含有标准基的同解方程组，转（2）。

（2）第二阶段：用第一阶段所得的含标准基的约束方程组取代原问题的约束方程组，再用单纯形法求解。

例1.10  试用两阶段单纯形法求解

解  第一阶段：由于原问题只有两个约束，且系数矩阵又有一个单位向量，故只需再引入一个人工变量y就可以获得单位矩阵，构造新规划如下：

 

本阶段的计算过程及结果见表1-15，在表1-15中，，人工变量全部为非基变量，原问题已得到标准基。

表1-15

cj	-1	0	0	0
初 始 表	y	x1	x2	x3	b
	1	（2）	1	0	4
	0	1.5	1	1	7
	0	2	1	0	4
最优表	0.5	1	0.5	0	2
	-0.75	0	0.25	1	4
	-1	0	0	0	0

 

第二阶段：去掉第一阶段结果中的人工变量y，剩余部分用以替换原问题的约束方程组，则可得原问题的等价形式为：

 

用单纯形法求解，其过程及结果见表1-16。从该表中，可以知道，原问题的最优解为

表1-16

cj	-1	1	-3
初 始 表	x1	x2	x3	b
	1	（0.5）	0	2
	0	0.25	1	4
	0	2.25	0	14
最优表	2	1	0	4
	-0.5	0	1	3
	-4.5	0	0	5

 

例1.11  求解线性规划

注意前两个约束实际是同一约束，故其中之一是多余约束，试观察多余约束是如何在迭代计算过程中被除去的。                         

解： 引入人工变量，构造新规划为

 

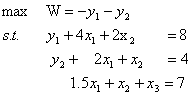
其计算过程及结果见表1-17。在表1-17中，，且行中，的系数以及全为零，故原问题的约束方程组等价于：

 

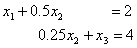
与例1.10第一阶段的最后结果完全相同。转入第二阶段后，其过程与结果也应与表1-16相同。

表1-17

cj	-1	-1	0	0	0
初 始 表	y1	y1	x1	x2	x3	b
	1	0	（4）	2	0	8
	0	1	2	1	0	4
	0	0	1.5	1	1	7
	0	0	6	3	0	12
	0.25	0	1	0.5	0	2
	-0.5	1	0	0	0	0
	-0.375	0	0	0.25	1	4
	-1.5	0	0	0	0	0

李 钦，关于线性规划问题退化解的教学思考，2022

Python实现两阶段法

Python代码

import numpy as np

import time

1、算法原理

首先设法找到一个（初始）基可行解，然百后再根据最优性条件判断这个基可行解是否最优解。若度是最优解，则输出结果，计算停止；若不是最优解，则设法由当前的基本可行解产生一个目标值更优的新的基本可行解，再利用最优性条件对所知得的新基可行解进行判断，看其是否最优解，这样就构成一个迭代道算法。由于基本可行解只有有限个，而每次目标值都有所改进，因而必可在有限步版内终止。如果原问题确有最优解，必可在有限步内达到；若原问权题无最优解，也可根据最优性理论及时发现，停止计算，避免错误及无效运算。

由于要解决等式约束，先添加人工变量，求解第一阶段的最小值；再删去人工变量列，添加z=cx的系数矩阵c。

2、两阶段法的主要结构

【求解类型】-最小化问题，等式约束与不等式约束（<=）

• 1. 主函数

if __name__ == '__main__':

    #问题求解

'''

Min Z=0.4*x1+0.5*x2+0*x3

st. 0.5*x1+0.5*x2=6

    0.6*x1+0.4*x2-x3=6

    0.3*x1+0.1*x2<=2.7

''' 

    c = np.array([-2,3,0,0])

    # 不等式约束<=

    A_ub = np.array([])

    b_ub = np.array([])

    # 等式约束

    A_eq = np.array([[1,-1,1,0],

                 [-3,1,0,1]])

    b_eq = np.array([2,4])

    time.perf_counter()

    digit = 2

    Problem=Simplex(c, A_ub, b_ub, A_eq, b_eq)

    Problem.Main()

    print('Running time: %s Seconds', time.perf_counter())

• 2.定义Simplex()大类

class Simplex(object):

    def __init__(self,c,A_ub,b_ub,A_eq, b_eq):  #初始化函数

        self.c=c            #系数矩阵

        self.A_ub=A_ub      #不等式约束矩阵

        self.b_ub=b_ub      #不等式约束边界

        self.A_eq=A_eq      #等式约束矩阵

        self.b_eq=b_eq      #等式约束边界

        self.N_x=0          #变量个数

        self.meq=0          #等式约束个数

        self.mub = 0        #不等式约束个数

        self.m=0            #约束的总数

        self.T=[]           #将所有数据放入单纯形表T

        self.sign=[]        #记录基变量序号

        self.F=1            #判断迭代进行的情况：

                            # 1——继续迭代

                            # 0——无界解，停止迭代

• 3. 将初值全部放入大矩阵T中

数据初始化函数：输入等式约束矩阵A_eq,b_eq，不等式约束矩阵A_ub,b_ub以及求解函数的系数矩阵c（当只有某一个约束时，用空矩阵[]代替）；将所有已知参数全部放入单纯形表矩阵T中。获得基变量列表sign

def Initial_value(self):

    self.N_x=len(self.c)

    # 按照约束类型求解

    if self.b_eq.any():  # 判断等式约束的有无

        self.meq = len(self.b_eq)

    if self.b_ub.any():  # 判断不等式约束的有无

        self.mub = len(self.b_ub)

    self.m = self.mub + self.meq  # 所有约束的行数

    # 建立第一阶段单纯型表。

    self.T = np.zeros([self.m + 1, self.N_x + self.m + 1], dtype='float')

    b = self.T[:-1, -1]

    # 判断两种约束的有无，

    # T矩阵上半部分为等式约束，下半部分为不等式约束

    if self.meq > 0:

        self.T[:self.meq, :self.N_x] = self.A_eq

        b[:self.meq] = self.b_eq

    if self.mub > 0:

        self.T[self.meq:self.m, :self.N_x] = self.A_ub

        b[self.meq:self.m] = self.b_ub

    #人工变量与松弛变量系数设为1

    np.fill_diagonal(self.T[:self.m, self.N_x:self.N_x + self.m], 1)

    # T矩阵最后一行表示（-c）

    # 第一阶段

    self.T[-1, self.N_x:self.N_x + self.meq] = -1 * np.ones(self.meq)

    for i in range(0, self.meq):

        self.T[-1] += self.T[i]

    l = [i for i in range(self.N_x, self.N_x + self.m)]  # 记录基变量列标,也可自行输入列标

    self.sign = list(l)

• 4. 最优性检验函数

由于是最小化，当非基变量检验数都小于等于0即可停止运算。1.先判断非基变量检验数是否都小于0，决定是否进行迭代运算；否则，进行迭代运算 def calculate()，每一次迭代只会让一个变量离基，一个变量进基。迭代次数由num统计。

def solve(self):  # 判断是否到达最优解

    num = 0

    flag = True

    while flag:

        # 直至所有非基变量检验数小于等于0

        # 合并多个解的情况，即使非基变量检验数等于0也停止迭代

        if max(list(self.T[-1][:-1])) <= 0:

            flag = False

        # 迭代，直至某个非基变量检验数等于0

        else:

            num += 1

            self.F=self.calculate()

        # 判断无界解，防止无限迭代

        if self.F==0:

            break

• 5.迭代函数：

选出最大的检验数，选出出该列bj/yj中最小的一行，变为1，进行迭代运算。运算过程中，用sign【】列表记录并更新基变量的序号。

def calculate(self): # 进行迭代运算

    H = list(self.T[-1, :-1])

    j_num = H.index(max(H))

    D = []

    for i in range(0, self.m):

        if self.T[i][j_num] == 0:

            D.append(float("inf"))

        else:

            D.append(self.T[i][-1] / self.T[i][j_num])

    if max(D) <= 0:# 判断无界解

        return 0

    # 找出最小比值所在行、列—i_num,j_num

    i_num = D.index(min([x for x in D if x >= 0]))

    self.sign[i_num] = j_num

    t = self.T[i_num][j_num]

• 高斯消元法换基迭代

#换基迭代

self.T[i_num] /= t

for i in [x for x in range(0, self.m + 1) if x != i_num]:

    self.T[i] -= self.T[i_num] * self.T[i][j_num]

return 1

• 6. 去人工变量

对于混合约束，需要采用两阶段法，去掉人工变量列，替换上最优化函数的系数的相反数-C。

两阶段衔接函数：

def change(self):#人工变量所在列变为0，替换上第二阶段的c

    self.T[:, self.N_x:self.N_x + self.meq] = 0

    self.T[-1, 0:self.N_x] = -self.c

    for i in range(0, self.m):

        self.T[-1] -= self.T[i] * self.T[-1][int(self.sign[i])]

• 7.两阶段法和单纯形法选择

两阶段法增加了等式约束，且两个阶段运算方法相同，可根据等式约束的有无决定是否进行第二阶段，不进行第二阶段则为常规单纯形法。

def Main(self):#主函数

    self.Initial_value()

    if self.meq > 0:  # 采用两阶段法

        # 第一阶段求解

        print("phase 1")

        self.solve()

        # 消去人工变量列

        self.change()

        #第二阶段求解

        print("phase 2")

        self.solve()

    else:

        # 直接进入第二阶段求解，消去人工变量列

        print("simple")

        self.change()

        self.solve()

    if self.F==1:

        print("Optimal solution:")

        j = 0

        for i in range(0, self.N_x):

            if i not in self.sign:

                print("x" + str(i + 1) + "=0")

            else:

                print("x" + str(i+1) + "=", self.T[j][-1])

                j+=1

        print("Best Value:\n", self.T[-1][-1])

    else:

        print("出现无界解")

• 8.求解结果

phase 1phase 2

Optimal solution :x1= 2.0

x2=0x3=0

x4= 10.0Best Value:-4.0

Running time: %s Seconds 0.239326

————————————————

原文链接：https://blog.csdn.net/zfdvxhbbnm/article/details/105599551