2.9 表格单纯形法
从上面求解例1的过程发现,直接使用单纯形法进行迭代计算不是很方便的,其中最复杂的是进行基变换,但施行基变换所用的实际上是消元法.由线性代数知道,用消元法解线性方程组可在增广矩阵上利用行初等变换进行计算.因此,可以将求解标准形线性规划的单纯形法的全部计算过程在一个类似增广矩阵的数表上进行,这种表称为单纯形表.在这种表格上进行的单纯形法运算称为表格单纯形法.
通常情况下,不妨假设\mathbf A的前m列线性无关,则单纯形表形式可以布局如下:
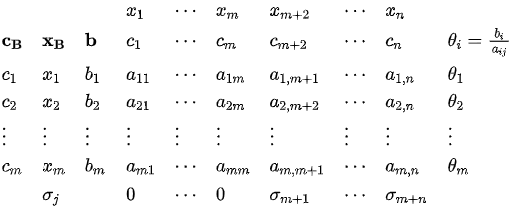
其中\mathbf {x_B},\mathbf{c_B}分别为基变量和其对应目标函数中的系数,\sigma_j为第j个变量的检验数.
例 2 使用表格单纯形法求解例1.
解 模型标准化后对应的初始单纯形表表示为

此时,\mathbf x =(0,0,0)^\top, z=0.选择x_1进基,x_5离基.

此时,\mathbf x =(3,0,0)^\top, z=-15.选择x_2进基,x_4离基.

此时,已得最优单纯形表,故得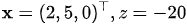 .
.
根据单纯形法解的判定定理2.3.1 2.3.3,也可从单纯形表格判定线性规划问题解的情况.
2.3.3,也可从单纯形表格判定线性规划问题解的情况.
随堂练程序表格单纯形法的Python实现
2.3.5 单纯形法的特点
2.3.5.1 计算复杂度
根据单纯形法的构建原理可知,它的迭代搜索过程始终沿着可行域的边界搜索,从可行域的一个顶点走向相邻的另一顶点,而可行域的顶点共有C_n^m个,当问题规模非常大(即变量非常多)的情况下,如n\ge 2m时,C_n^m\ge\left(\frac{n}{m}\right)^m\ge 2^m,单纯形法的算法运算量可能达到指数阶.事实上,Klee 和 Minty (1972) 给出了一个例子,在该例子中单纯形算法需要遍历2^m个顶点才能获得最优解.由此可知,单纯形算法不是.
经验表明,单纯形算法求解某些问题确实会比较慢.不过,实际上单纯形算法求解问题的平均效率却很高,求解中小规模的问题非常快,一般不会超过4m至6m次迭代(包括获得初始可行解在内).从单纯形算法不是多项式时间的却依然有较好的实际表现说明,依据最坏情况下的计算复杂度参考价值有限,甚至可能会产生一些误导.因为这些最坏情况在实际问题中几乎不可能发生,而在合理概率意义下的复杂度才更加贴近现实情况.Borgwardt(1982) 证明单纯形算法的平均复杂度是多项式时间的.
2.3.5.2 退化和循环
若单纯形表中的基本可行解中出现一个或多个基变量等于零时,或者按最小比值来确定换出基的变量时,存在两个以上相同最小比值的线性规划问题,称之为退化问题.
退化情况会使得在单纯形法的进基和离基操作无效,导致在完成一次进基和离基操作后,目标函数的值不会发生变化,但是基会发生变化.
例如线性规划问题 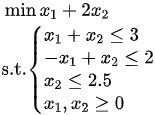 ,其可行域如图 2-3-2所示.
,其可行域如图 2-3-2所示.
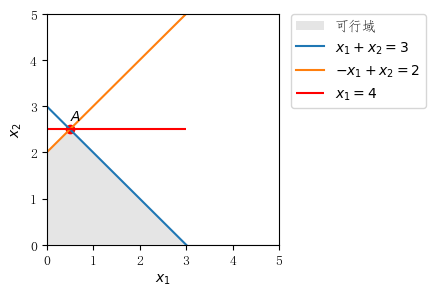
图2-3-2线性规划退化问题
从中可以发现顶点A=(0.5,2.5)^\top是三个约束对应直线的交点,通常情况下,二条直线相交可以得到一个顶点,但是本问题中恰好三条线交于同一顶点.
将其化为标准形式为
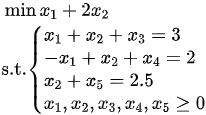 .
.
而顶点A=(0.5,2.5)^\top在标准形中对应的基为
\mathbf v=\left(0.5, 2.5, 0, 0, 0\right)^\top,
显然顶点A对应的基变量可以有三种情况:x_1,x_2,x_3,x_1,x_2,x_4,x_1,x_2,x_5.例如从基变量x_1,x_2,x_3出发,令x_3出基x_4离基,那么得到新基变量x_1,x_2,x_4,但是这两组基对应顶点未变,仍是顶点A.
当没有退化现象发生的时候,单纯形法在搜索过程中可以保证某个非基变量检验数\sigma_i<0,由此可知单纯形算法必然不会搜索已经搜索过的顶点(即不可能产生循环).反之,当有退化现象发生的时候,单纯形法在搜索过程中可能会使得某个\sigma_i=0,由此可知单纯形算法可能会再次搜索已经搜索过的顶点(即可能产生循环).一旦产生循环现象,就无法找到最终的最优解.
Beale在1955年提出了一个如下的线性规划问题
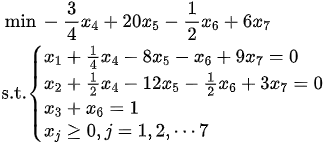 ,
,
其最优解为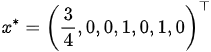 ,最优值为
,最优值为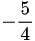 .但按照基本的单纯形法求解过程中会出现循环,从而不能找到最优解.
.但按照基本的单纯形法求解过程中会出现循环,从而不能找到最优解.
针对退化和循环问题,已经有多种方法解决这类问题.

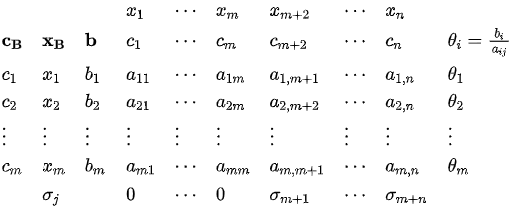



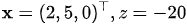 .
. 2.3.3,也可从单纯形表格判定线性规划问题解的情况.
2.3.3,也可从单纯形表格判定线性规划问题解的情况.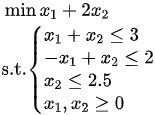 ,
,
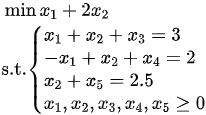 .
.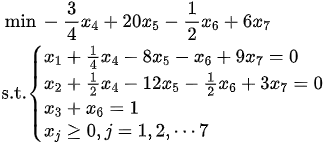 ,
,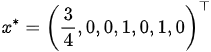 ,最优值为
,最优值为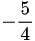 .但按照基本的单纯形法求解过程中会出现循环,从而不能找到最优解.
.但按照基本的单纯形法求解过程中会出现循环,从而不能找到最优解.
