六、最大化单纯形法  

2.8 单纯形法步骤

下面以极小化问题为例给出单纯形法计算步骤．

求解线性规划标准形的单纯形法

Step 1 确定初始基本可行解．

Step 2 检验各非基变量的检验数．如果\sigma_j≥0(j=m+1,⋯,1)，则当前的基本可行解就是最优解，算法结束；否则转Step 3．

Step 3 如果存在\sigma_j<0使得其对应变量x_j的系数列向量\mathbf p_j≤，即\mathbf p_j的每个分量均为非正数，则线性规划问题的解无界，算法结束；否则转Step 4．

Step 4 设\sigma_k=\displaystyle\min⁡_j\{\sigma_j\}<0，选取x_k为入基变量．根据l=\mathop{\text{argmin}}\limits_i \left\{\theta_i=\displaystyle\frac{b_i'}{a_{ij}'}\Big|a_{ij}'>0 \right\}确定l，选取x_l为离基变量．转Step 5．

Step 5 以a_{lk}'为主元旋转运算，即利用行变换将第k个系数列向量变换为a_{lk}'=1，其它元素为0．转Step 2．

下面给出应用单纯形法求解问题（2.3.1）的完整过程．

例 1 用单纯形法求解

\begin{aligned} &\min z =-5x_1-2x_2\\ &\text{s.t.}\begin{cases} 30x_1+20x_2+x_3≤160\\ 5x_1+x_2≤15\\ x_1 ≤4\\ x_i≥0,~i=1,2,3 \end{cases}. \end{aligned}

解 通过引入3个非负松驰变量x_4,x_5,x_6，把模型标准化为

\begin{aligned} &\min z=-5x_1-2x_2\\ &\text{s.t.}\begin{cases} 30x_1+20x_2+x_3 + x_4&&=160\\ 5x_1+x_2 &+x_5 &=15\\ x_1 &&+x_6 =4\\ x_i≥0,~i=1,2,\cdots,6 \end{cases} \end{aligned}，

则\mathbf A=\begin{pmatrix} 30 & 20 & 1 & 1& 0 &0\\5&1 & 0& 0 & 1 &0\\ 1 & 0 & 0 & 0 & 0&1\end{pmatrix}，\mathbf b=\begin{pmatrix} 160\\15\\ 4\end{pmatrix}，\mathbf c^\top=\begin{pmatrix} -5,-2,0,0,0,0\end{pmatrix}．

• 第1次迭代．

（1）确定初始基本可行解．

取基矩阵\mathbf B=(\mathbf p_4,\mathbf p_5,\mathbf p_6)=\begin{pmatrix}  1& 0 &0\\ 0 & 1 &0\\  0 & 0&1\end{pmatrix}，非基矩阵\mathbf N=(\mathbf p_1,\mathbf p_2,\mathbf p_3)=\begin{pmatrix} 30 & 20 & 1 \\5&1 & 0\\ 1 & 0 & 0 \end{pmatrix}，则\mathbf{x_B}=(x_4,x_5,x_6)^\top，\mathbf{x_N}=(x_1,x_2,x_3)^\top，即

\begin{cases} x_4 = 160-(30x_1+20x_2+x_3)\\ x_5 = 15-(5x_1+x_2 )\\ x_6=4-x_1 \end{cases}．

而\mathbf{c_B}=(c_4,c_5,c_6)^\top=(0,0,0)^\top，\mathbf{c_N}=(c_1,c_2,c_3)^\top=(-5,-2,0)^\top．

令\mathbf{x_N}=\mathbf 0，则\mathbf{x_B}=(160，15，4)^\top，即\mathbf x^{(0)}=(0,0,0,160,15,4)^\top，代入目标函数得z_0=\mathbf{c^\top x}=0．

（2）检验各非基变量的检验数．

(\sigma_1,\sigma_2,\sigma_3)=\mathbf{c_N^\top}-\mathbf{c_B^\top}\mathbf{B}^{-1}\mathbf N=(-5,-2,0)-(0,0,0)\begin{pmatrix} 1& 0 &0\\ 0 & 1 &0\\ 0 & 0&1\end{pmatrix}\begin{pmatrix} 30 & 20 & 1 \\5&1 & 0\\ 1 & 0 & 0 \end{pmatrix}=(-5,-2,0)，

其中\sigma_i<0(i=1,2)，所以\mathbf{x_B}=(160，15，4)^\top不是最优解．

（3）此时\mathbf p_i\ge\mathbf 0(i=1,2)，所以继续计算．因为\min\{\sigma_1,\sigma_2\}=\sigma_{\textcolor{red}{1}}=-5，故选择x_1进基；而

\theta=\displaystyle\min⁡\left\{\frac{b_i}{a_{ik}}\Big|a_{ik}>0\right\}=\min⁡\left\{\frac{160}{30},\frac{15}{5}\right\} =\frac{b_{\textcolor{red}{2}}'}{a_{\textcolor{red}{2}1}'}=5，

此时对应第2个基变量，其下标为5，故选择x_5离基．

（4）以a_{\textcolor{red}{21}}'为主元旋转运算．

\begin{aligned}\mathbf A&=\left(\begin{array}{c:c}\begin{matrix}30 & 20 & 1 & 1& 0 &0\\\textcolor{red}{5}&1 & 0& 0 & 1 &0\\ 1 & 0 & 0 & 0 & 0&1\end{matrix}&\begin{matrix}160\\50\\4 \end{matrix}\end{array}\right)\\&\rightarrow\left(\begin{array}{c:c}\begin{matrix}0 & 14 & 1 & 1& -6 &0\\\textcolor{red}{1}&1/5 & 0& 0 & 1/5 &0\\ 0 & -1/5 & 0 & 0 & -1/5&1\end{matrix}&\begin{matrix}70\\3\\1\end{matrix}\end{array}\right)\triangleq\mathbf A_1\end{aligned}\qquad\qquad，

此时得\mathbf x^{(1)}=(3,0,0,70,0,1)^\top，z_1=-15．

显然此时的目标函数值z_1比z_0下降了．

• 第2次迭代．

此时，从\mathbf A_1中取基矩阵\mathbf B=(\mathbf p_4,\mathbf p_1,\mathbf p_6)=\begin{pmatrix}  1& 0 &0\\ 0 & 1 &0\\  0 & 0&1\end{pmatrix}，\mathbf{x_B}=(x_4,x_1,x_6)^\top，非基矩阵\mathbf N=(\mathbf p_5,\mathbf p_2,\mathbf p_3)=\begin{pmatrix} -6 & 14 & 1 \\1/5&1/5 & 0\\ -1/5 & -1/5 & 0 \end{pmatrix}，\mathbf{x_N}=(x_5,x_2,x_3)^\top，\mathbf{c_B}=(c_4,c_1,c_6)^\top=(0,-5,0)^\top，\mathbf{c_N}=(c_5,c_2,c_3)^\top=(0,-2,0)^\top．然后重复上面的（2）~（4）．

因为非基变量检验数

\begin{aligned}(\sigma_5,\sigma_2,\sigma_3)&=\mathbf{c_N^\top}-\mathbf{c_B^\top}\mathbf{B}^{-1}\mathbf{N}\\&=(0,-2,0)-(0,-5,0)\begin{pmatrix} 1& 0 &0\\ 0 & 1 &0\\ 0 & 0&1\end{pmatrix}\begin{pmatrix} -6 & 14 & 1 \\1/5&1/5 & 0\\ -1/5 & -1/5 & 0 \end{pmatrix}\\&=(1,-1,0)\end{aligned}，

其中只有\sigma_2=-1<0，所以x_2进基；又由增广矩阵\mathbf A'可知，\theta=\displaystyle\min⁡\left\{\frac{70}{14},\frac{3}{1/5}\right\} =\frac{b_{\textcolor{red}{1}}'}{a_{\textcolor{red}{1}2}'}，此时对应第1个基变量，其下标为4，可知\mathbf x_4离基．再以a_{\textcolor{red}{12}}为主元旋转运算．

\mathbf A_1=\left(\begin{array}{c:c}\begin{matrix}0 & 14 & 1 & 1& -6 &0\\{1}&1/5 & 0& 0 & 1/5 &0\\ 0 & -1/5 & 0 & 0 & -1/5&1\end{matrix}&\begin{matrix}70\\3\\1\end{matrix}\end{array}\right)\qquad\qquad\rightarrow\left(\begin{array}{c:c}\begin{matrix}0 & 1 & 1/14 & 1/14& -3/7 &0\\{1}&0 & -1/70& -1/70 & 0 &0\\ 0 & 0 & 1/70 & 1/70 & 1&1\end{matrix}&\begin{matrix}5\\2\\2\end{matrix}\end{array}\right)\triangleq\mathbf A_2，

得\mathbf x^{(2)}=(2,5,0,0,0,2)^\top，z_1=-20．

此时基变量为x_2,x_1,x_6，则非基变量x_3,x_4,x_5检验数

\begin{aligned}(\sigma_3,\sigma_4,\sigma_5)&=\mathbf{c_N^\top}-\mathbf{c_B^\top}\mathbf{B}^{-1}\mathbf{N}\\&=(0,0,0)-(-2,-5,0)\begin{pmatrix} 1& 0 &0\\ 0 & 1 &0\\ 0 & 0&1\end{pmatrix}\begin{pmatrix} 1/14 & 1/14& -3/7\\-1/70& -1/70 & 0\\ 1/70 & 1/70 & 1 \end{pmatrix}\\&=\displaystyle\left(\frac{1}{14},\frac{1}{14},0\right)\ge \mathbf 0,\end{aligned}

所以迭代停止，\mathbf x=(2,5,0)^\top为最优解，最优值z=-20．

图 2-3-1附录 / 附录程序‌显示了本例中单纯形法迭代过程．问题的可行域为三维空间的凸多面体，可以发现，每次迭代总是沿着可行域的边界搜索，即从凸多面体的一个顶点走向相邻的另一顶点．

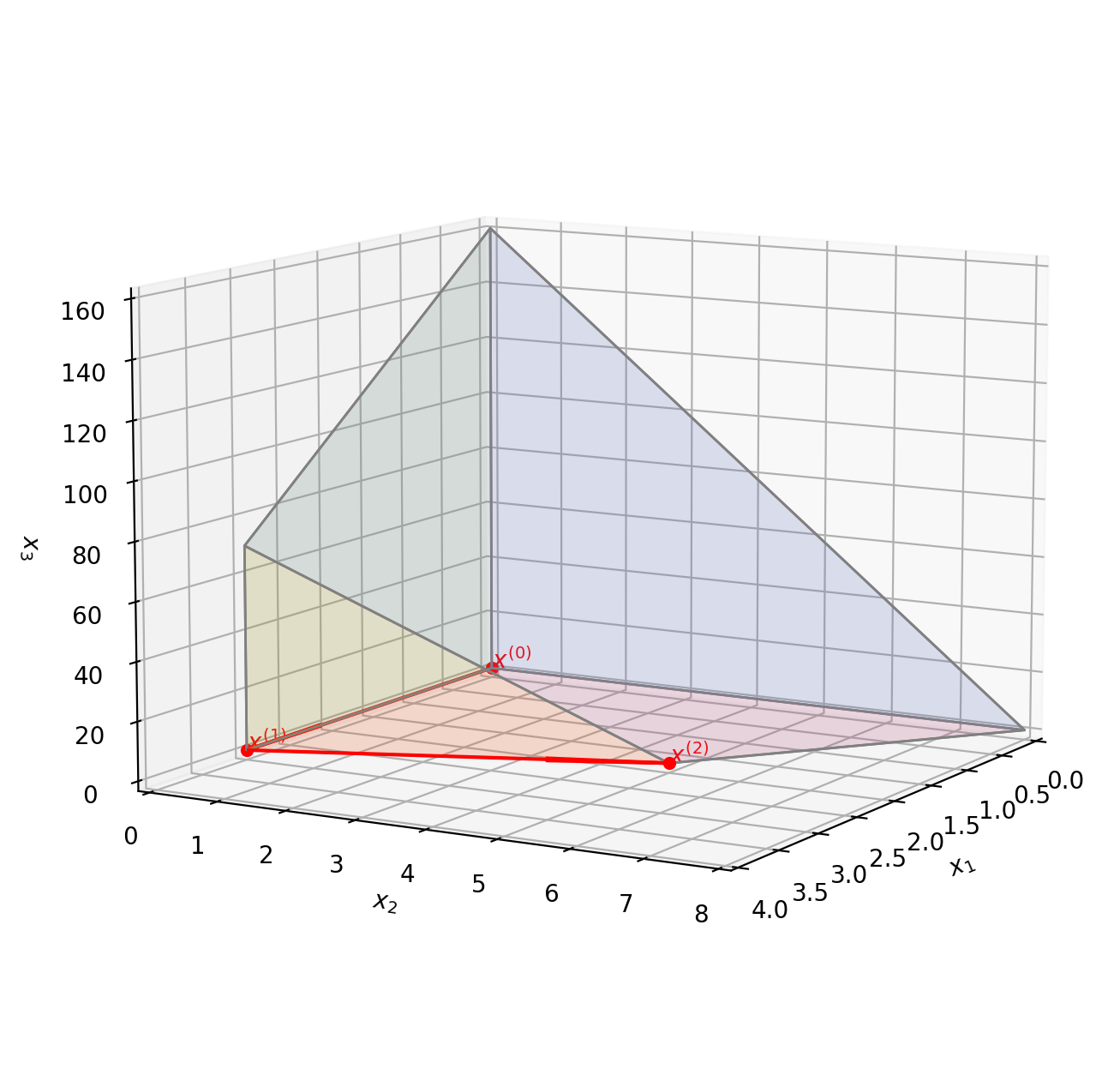
图2-3-1单纯形法每次迭代总是沿着凸多面体的棱前进的

说明：对于目标函数极大化、约束为标准型的线性规划问题，在利用单纯形方法求解时，与极小化过程一致，不同之处是检验是否最优的判定准则和进基准则不同．即

• 若某个基本可行解的所有非基变量对应的检验数\sigma_{\mathbf N}= \mathbf C_{\mathbf N} − \mathbf C_\mathbf {BN}≤0，则基本可行解为最优解．

• 采用最大增加原则（而非最大减少原则）来确定进基变量．即\displaystyle\max_{j}\{\sigma_j>0|+1≤≤\}，则选取对应的非基变量x_j为进基变量．

• 出基变量仍采用（非负）最小比值原则来确定．

单纯形法程序实现

针对模型

min cx; 

s.t. A_ub*x<=B_ub

      A_eq*x=b_eq

      lb<=x<=ub

python 内置命令：scipy库中optimize

from scipy import optimize as op

import numpy as np

'''

求解 

min cx
s.t. A_ub*x<=B_ub,
A_eq*x=b_eq, 

c指的应该是要求最大值的函数的系数数组，
A_ub是应该是不等式未知量的系数矩阵，仔细观察的人应该发现，为什么第一行里面写的是[-2,5,-1]而不是[2,5,-1]呢，应该要与图里对应才对啊，原来这不等式指的是<=的不等式，那如果是>=呢，乘个负号就行了。
A_eq就是其中等式的未知量系数矩阵了。
B_ub就是不等式的右边了，B_eq就是等式右边了。
bounds的话，指的就是每个未知量的范围了。

'''

#%% 

c=np.array([2,3,-5])

A_ub=np.array([[-2,5,-1],[1,3,1]])

B_ub=np.array([-10,12])

A_eq=np.array([[1,1,1]])

B_eq=np.array([7])

x1=(0,7)

x2=(0,7)

x3=(0,7)

res=op.linprog(-c,A_ub,B_ub,A_eq,B_eq,bounds=(x1,x2,x3))

print(res)

python 实现解线性规划的单纯形法

import numpy as np

#%%% 转轴运算

def pivot(): 

    l = list(d[0][:-1])  

    jnum = l.index(max(l)) #转入编号

    m = []

    for i in range(bn):

        if d[i][jnum] == 0:

            m.append(0.)

        else:

            m.append(d[i][-1]/d[i][jnum])

    inum = m.index(min([x for x in m[1:] if x!=0]))  #转出下标

    s[inum-1] = jnum #更新基变量

    #更新d

    r = d[inum][jnum]

    d[inum] /= r

    for i in [x for x in range(bn) if x !=inum]:

        r = d[i][jnum]

        d[i] -= r * d[inum]

###% 求解    

def solve():

    flag = True

    while flag:

        if max(list(d[0][:-1])) <= 0: #直至所有系数小于等于0

            flag = False

        else:

            pivot()

###% 打印结果 

def printSol():

    for i in range(cn - 1):

        if i in s:

            print("x"+str(i)+"=%.2f" % d[s.index(i)+1][-1])

        else:

            print("x"+str(i)+"=0.00")

    print("objective is %.2f"%(-d[0][-1]))

if __name__ == "__main__":

    '''

        max z=x0+14∗x1+6∗x2

        s.t.x0+x1+x2≤4 

        x0≤2

        x2≤3

        3∗x1+x2≤6 

    '''

    # d数组第0行是c，最后一列是b，其余是A

    d = np.array([[ 1., 14.,  6.,  0.,  0.,  0.,  0.,  0.],

         [ 1.,  1.,  1.,  1.,  0.,  0.,  0.,  4.],

         [ 1.,  0.,  0.,  0.,  1.,  0.,  0.,  2.],

         [ 0.,  0.,  1.,  0.,  0.,  1.,  0.,  3.],

         [ 0.,  3.,  1.,  0.,  0.,  0.,  1.,  6.]])

    (bn,cn) = d.shape

    s = list(range(cn-bn,cn-1)) #基变量列表

    solve()

    printSol()

Matlab实现

matlab内置命令: linprog

>> c = [-5; -4; -6];

>> A = [1 -1  1;3  2  4;3  2  0];

>> b = [20; 42; 30];

>> lb = [0; 0; 0];

>> [x,fval,exitflag,output,lambda] = linprog(c,A,b,[],[],lb)

matlab实现单纯形法

function main()
A = [2 1 1 0; 1 3 0 1];
b = [40; 30];
c = [3 4 0 0];
ind = [3 4];
[x, z, ST, ca] = SimplexMax(c, A, b, ind)

function [x,z,ST,res_case] = SimplexMax(c,A,b,ind_B)
% 单纯形法求解标准形线性规划问题: max cx s.t. Ax=b x>=0
% 输入参数: c为目标函数系数, A为约束方程组系数矩阵, 
%             b为约束方程组常数项, ind_B为基变量索引
% 输出参数: x最优解, z最优目标函数值, ST存储单纯形表数据, 
%             res_case=0表示有最优解，res_case=1表示有无界解

[m,n] = size(A);              %m约束条件个数, n决策变量数
ind_N = setdiff(1:n, ind_B);  %非基变量的索引
ST = [];
format rat
% 循环求解
while true
    x0 = zeros(n,1);
    x0(ind_B) = b;               %初始基可行解
    cB = c(ind_B);               %计算cB
    Sigma = zeros(1,n);
    Sigma(ind_N) = c(ind_N) - cB*A(:,ind_N);   %计算检验数
    [~, k] = max(Sigma);         %选出最大检验数, 确定进基变量索引k
    Theta = b ./ A(:,k);         %计算θ
    Theta(Theta<=0) = 10000;
    [~, q] = min(Theta);         %选出最小θ
    el = ind_B(q);               %确定出基变量索引el, 主元为A(q,k)
    vals = [cB',ind_B',b,A,Theta];
    vals = [vals; NaN, NaN, NaN, Sigma, NaN];
    ST = [ST; vals];
    if ~any(Sigma > 0)           %此基可行解为最优解, any存在某个>0        
        x = x0;
        z = c * x;
        res_case = 0;
        return
    end
    if all(A(:,k) <= 0)          %有无界解
        x = [];
        res_case = 1;
        break
    end
    % 换基
    ind_B(ind_B == el) = k;      %新的基变量索引
    ind_N = setdiff(1:n, ind_B); %非基变量索引
    % 更新A和b
    A(:,ind_N) = A(:,ind_B) \ A(:,ind_N);
    b = A(:,ind_B) \ b;
    A(:,ind_B) = eye(m,m);
end

20世纪十大算法之一—— 单纯形法 （Simplex)  

    单纯形法是求解线性规划的一种有效方法，该方法被誉为20世纪十大算法之一，还有资料说，它是20世纪创造经济效益最多的算法。这是可以理解的，因为在社会生产系统中会大量遇到这种决策问题。比如，中国石化在全国有成千上万个加油站，那么如何布局这些加油站可以使运行成本最低呢？油料运输中，走何种路线、在何处中转可以最节约成本呢？要回答这些问题，并不是拍拍脑袋就可以解决的。单纯形法就可以回答这种问题，帮助人们找到最优的解决方案，从而大幅度降低运行成本。 

    单纯形法的发明简直是一个传奇。

    当时，G.B.Dantzig（丹齐克，1914-2005）还是一个学生。一天，他匆匆忙忙赶到教室，但还是迟到了。他看到黑板上有几道题目，就赶快抄了下来，回家后拼死拼活做了几个礼拜。然后交给老师，并表示万分的歉意，说题目太难了，所以现在才交。几天之后，老师把丹齐克叫过去，说他太兴奋了。原来，那些题目根本不是家庭作业，而是本领域尚未解决的几个问题。丹齐克给出的解法正是享誉世界的单纯形法。

发展简史

原始单纯形法

    线性规划问题是研究在线性约束条件下，求线性函数的极值问题。线性规划是运筹学的一个重要分支， 也是最早形成的一个分支。线性规划的最优性条件，又称为Karush-Kuhn-Tucker(KKT)条件。不等式约束问题的必要和充分条件初见于卡罗需(William Karush)的博士论文，之后在一份由W.库恩(Harold W. Kuhn)及塔克(Albert W. Tucker)撰写的研讨生论文出现后受到重视。

    线性规划的集大成者是G.B.丹齐克(George Bernard Dantzig)。1947 年，面对美国制定空军军事规划时提出的问题，丹齐克首次提出了单纯形法来解决这类极值问题的求解。单纯形法是年由创建的对所有一般线性规划问题的最早的可行算法。1953年，他又提出了改进单纯形法。

    但原单纯形法不是很经济的算法。许多数学家在随后提出更有效率的算法，如改进单纯形法、对偶单纯形法等。

改进单纯形法

    1953年美国数学家G.B.丹齐克为了改进单纯形法每次迭代中积累起来的进位误差，提出改进单纯形法。其基本步骤和单纯形法大致相同，主要区别是在逐次迭代中不再以高斯消去法为基础，而是由旧基阵的逆去直接计算新基阵的逆，再由此确定检验数。这样做可以减少迭代中的累积误差，提高计算精度，同时也减少了在计算机上的存储量。

对偶单纯形法

    1954年美国数学家C.莱姆基提出对偶单纯形法(Dual Simplex Method)。单纯形法是从原始问题的一个可行解通过迭代转到另一个可行解，直到检验数满足最优性条件为止。对偶单纯形法则是从满足对偶可行性条件出发通过迭代逐步搜索原始问题的最优解【参见第3章，对偶规划】。在迭代过程中始终保持基解的对偶可行性，而使不可行性逐步消失。设原始问题为

，

则其对偶问题（Dual Problem）为

  。

当原始问题的一个基解满足最优性条件时，其检验数。即知（称为单纯形算子）为对偶问题的可行解。所谓满足对偶可行性，即指其检验数满足最优性条件。因此在保持对偶可行性的前提下，一当基解成为可行解时，便也就是最优解。