2.7 单纯形法原理
2.7.1 提出单纯形的思路
由上节知识可知，线性规划(LP)问题如果有最优解，那么最优解是可行域的某个极点（基本可行解）．一个朴素的想法是：通过枚举找出LP问题的所有基本可行解，然后逐个比较确定最优解．但枚举法时间花费会非常大，假设原问题中有n个变量，m个约束条件，则需要时间为C^{m}_{n}，而C^{m}_{n}会随着m和n的增大而迅速地增大．显然，这是不可行的．
换个角度考虑，若从某一基本可行解出发，每次总是寻求比上一个更“好”的基本可行解，直至找到最优解．这样就可以大大减少计算量．如果要使用这种迭代的求解方法，我们需要解决下面的三个问题：
（1）如何得到一个初始的基本可行解（迭代起点）；
（2）如何寻找下一个改善的基本可行解（迭代关系式）；
（3）如何判断当前的基本可行解是最优解（迭代终点）．
美国数学家（G.B.Dantzig）解决了上面的三个问题，也就得到了一种快速求解LP问题的方法，称为单纯形法．
2.7.2 单纯形法的基本过程
单纯形法是基于求解线性方程组构造的，因此需要标准化LP问题．下面结合2.1节中的引例进行分析．将引例中的模型标准化后为
\begin{aligned}
\min\ z=\mathbf c^\top \mathbf x\\
\text{s.t.}
\left\{ \begin{gathered} \mathbf{Ax}=\mathbf b \\ \mathbf x\geq \mathbf 0 \\ \end{gathered} \right.
\tag{2.3.1}\end{aligned}
其中，\mathbf c=\begin{pmatrix}-5\\ -2\\0\\ 0\\ 0\end{pmatrix}，\mathbf x=\begin{pmatrix}x_1\\x_2\\x_3\\x_4\\x_5\end{pmatrix}，\mathbf A=\left(a_{ij}\right)_{3\times 5}=\begin{pmatrix}30&20&1&0&0\\5&1&0&1&0\\1&0&0&0&1\\ \end{pmatrix}，\mathbf b=\begin{pmatrix}b_1\\b_2\\b_3\end{pmatrix}=\begin{pmatrix}160\\15\\4\end{pmatrix}．令\mathbf B_0=(\mathbf p_3,\mathbf p_4,\mathbf p_5)=\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}为基矩阵，即x_3,x_4,x_5为基变量，x_1,x_2为非基变量． 若用非基变量表示基变量，有
\begin{cases} &x_3=160-30x_1-20x_2 \\ &x_4=15-5x_1-x_2 \\ &x_5=4-x_1 \\ \end{cases}，
此时目标函数用非基变量表示为z=5x_1+2x_2．
若令x_1=0,x_2=0，则得到一个基本可行解为\mathbf x^{(0)}=(0,0,160,15,4)^\top，目标函数z^{(0)}=0，显然这不是最优解．那么便需要换一组基变量（即从可行域的一个顶点移动到另一个顶点），于是，选取x_1,x_2中的一个变量作为进基变量、x_3,x_4,x_5中的一个变量作为离基变量，进行换入换出．
现在，假设进基变量为x_1，下面确定离基变量．由于x_2仍为非基变量，故x_2仍取零值．因此，有
\begin{cases}x_3=160-30x_1 \\x_4=15-5x_1 \\x_5=4-x_1 \\\end{cases} .
由于\mathbf x\geq 0，所以在\displaystyle\left\{\frac{b_1}{a_{11}},\frac{b_2}{a_{21}},\frac{b_3}{a_{31}}\right\}=\displaystyle\left\{\frac{160}{30},\frac{15}{5},\frac{4}{1}\right\}中取最小可以保证变量非负，而\min\displaystyle\left\{\frac{b_1}{a_{11}},\frac{b_2}{a_{21}},\frac{b_3}{a_{31}}\right\}=\displaystyle\frac{15}{5}对应变量为x_4，故选x_4为离基变量，这样得到一个新的基本可行解\mathbf x^{(1)}=(3,0,70,0,1)^\top，相应的基矩阵\mathbf B_1=(\mathbf p_3,\mathbf p_1,\mathbf p_5)，基变量为x_3,x_1,x_5，非基变量为x_2,x_4，对应的目标函数值z^{(1)}=-15 < z^{(0)}=0，因此，\mathbf x^{(1)}是比\mathbf x^{(0)}有改善的基本可行解．
下面分析\mathbf x^{(1)}是否是最优解．根据约束方程组，可以得到\displaystyle{x_1=3-\frac{1}{5}x_2-\frac{1}{5}x_4}，代入目标函数式，得到
z=5x_1+2x_2 = -15-x_2+x_4.
观察上面等式最右端，发现非基变量x_2前的系数为-1，若增大x_2，目标函数值仍可以减小，或者说，让x_2为进基变量，进行换入，有可能使目标函数值减小．因此，\mathbf x^{(1)}不是最优解．
使用相同的方法，以x_2为进基变量，得到x_3为离基变量，得到新的基本可行解\mathbf x^{(2)}=(2,5,0,0,2)^\top，目标函数
z=-20+\displaystyle\frac{1}{14}x_3+\frac{4}{7}x_4,
从上面等式右端可以看出，若非基变量x_3或x_4由零逐渐变大，则会使得目标函数值z也变大，故\mathbf x^{(2)}是最优解．
下面归纳一下单纯形法的基本解题步骤并分析每步的详细过程．
第一步：构造一个初始的基本可行解．
第二步：判断当前基本可行解是否为最优解．
第三步：若当前解不是最优解，则要进行基变换迭代到下一个基本可行解．
2.7.2.1 确定初始的基本可行解
不妨假设在形如标准型线性规划问题（2.3.1）中，系数矩阵\mathbf A中前m个系数列向量恰好构成一个可行基，即\mathbf A=(\mathbf B,\mathbf N)，其中矩阵\mathbf B=(\mathbf p_,\mathbf p_,⋯,\mathbf p_)为基变量x_1,x_2,…,x_m的系数列向量构成的可行基，\mathbf N=(\mathbf p_{+},\mathbf p_{+},⋯,\mathbf p_)为非基变量x_{+},x_{+}, …,x_{+}的系数列向量构成的矩阵．所以约束方程\mathbf{Ax}=\mathbf b可以表示为
\mathbf{Ax} =(\mathbf B,\mathbf N)(\mathbf {x_B},\mathbf {x_N})^\top=\mathbf B\mathbf {x_B}+\mathbf{Nx_N}=\mathbf b,
得\mathbf {x_B}=\mathbf B^{−1} \mathbf b−\mathbf B^{−1} \mathbf N\mathbf {x_N}．
若令所有非基变量\mathbf {x_N=0}，则基变量\mathbf {x_B} =\mathbf B^{−} \mathbf b，由此可得初始的基本可行解\mathbf x=(\mathbf B^{−1}\mathbf {b,0})^\top．
若将目标函数中基变量和非基变量的系数分别记为\mathbf{c_B}和\mathbf{c_N}，则将初始的基本可行解代入目标函数，得目标函数值
z=\mathbf c^\top\mathbf x=(\mathbf{c_B^\top,c_N^\top})(\mathbf B^{−1}\mathbf {b,0})^\top=\mathbf{c_B^\top}\mathbf B^{−1}\mathbf b.
2.7.2.2 判断现行的基本可行解是否最优
如何判定=\mathbf{C_B}- \mathbf B^{−1}\mathbf b是否已经达到最小值？设约束方程组
\begin{cases} a_{11}x_1 + a_{12}x_2 + \cdots+ a_{1n}x_n = b_1\\ a_{21}x_1 + a_{22}x_2 + \cdots+ a_{2n}x_n = b_2 \\ \cdots \ \cdots\\ a_{m1}x_1 + a_{m2}x_2 + \cdots+ a_{mn}x_n = b_m\\ \end{cases}
经过消元法迭代后有
\begin{cases}
x_1=b_1'-\displaystyle\sum_{j=m+1}^n a_{1j}'x_j\\
x_2=b_2' -\displaystyle\sum_{j=m+1}^n a_{2j}'x_j\\
\cdots \ \cdots\\
x_m=b_m' -\displaystyle\sum_{j=m+1}^n a_{1j}'x_j\\
\end{cases},\tag{2.3.2}
再将式（2.3.2）代入目标函数中得
\begin{aligned}\min z
&=\sum_{i=1}^m c_i\left(b_i'-\sum_{j=m+1}^n a_{ij}'x_j\right)+\sum_{j=m+1}^n c_jx_j\\
&=\sum_{i=1}^m c_i b_i' -\sum_{i=1}^m c_i \left( \sum_{j=m+1}^n a_{ij}'x_j\right)+\sum_{j=m+1}^n c_jx_j\\
&=\sum_{i=1}^m c_i b_i' -\sum_{j=m+1}^n \left( \sum_{i=1}^m c_ia_{ij}'x_j\right)+\sum_{j=m+1}^n c_jx_j\\
&=\sum_{i=1}^m c_i b_i' +\sum_{j=m+1}^n \left( \color{red}{c_j-\sum_{i=1}^m {c_ia_{ij}'}} \right) x_j.
\end{aligned}
令z_0=\displaystyle\sum_{i=1}^m c_ib_i'，\sigma_j=c_j-\displaystyle\sum_{i=1}^m c_i a_{ij}'，则有
z=z_0+\sum_{j=m+1}^n \sigma_jx_j. \tag{2.3.3}
称\sigma_j为非基变量x_j的检验数，所有非基变量的检验数也可用向量的形式表示为\boldsymbol\sigma= \mathbf{c_N^\top}-\mathbf{c_B^\top B}^{-1}\mathbf N．
于是可写出问题（2.3.1）对应的典式
\begin{aligned}&\min z_0+\sum_{j=m+1}^n \sigma_jx_j\\
&\text{s.t.}\begin{cases}
x_1=b_1'-\displaystyle\sum_{j=m+1}^n a_{1j}'x_j\\
x_2=b_2' -\displaystyle\sum_{j=m+1}^n a_{2j}'x_j\\
\cdots \ \cdots\\
x_m=b_m' -\displaystyle\sum_{j=m+1}^n a_{1j}'x_j\\
x_i\ge0,~i=1,2,\cdots,n
\end{cases}\end{aligned}
基于典式，可以根据\sigma_j来判断当前解是否是最优解．容易得出标准形线性规划问题（2.3.1）如下的解的判定定理2.3.1
2.3.2．
定理2.3.1 （最优性定理）若所有非基变量的检验数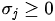
成立，则当前基本可行解\mathbf x^*就是最优解．
实际上，有些LP问题无解或者会有无穷多个解．这两类情况有些特殊，需要在迭代中进行额外的判断，防止算法陷入死循环或者出错．
定理 2.3.2 （无穷多个最优解的判定）如果当前基本可行解\mathbf {\bar x}的所有非基变量的检验数\sigma_j满足\sigma_j\geq 0，且其中一个\sigma_l=0，则该LP问题有无穷多个最优解．
定理 2.3.3 （无界解的判定）如果当前基本可行解\mathbf {\bar x}，其中一个非基变量x_l的检验数\sigma_l< 0，且x_j对应的系数列向量\mathbf p_l=(a_{1l},a_{2l},...,a_{ml})^\top的所有分量a_{il}\leq 0(i=1,2,\cdots,m)，则该线性规划问题具有无界解（或者称无最优解）．
证明 设非基变量中的某个变量x_l\ne 0，其它x_j=0(j\ne l)，由式
\displaystyle\begin{cases}x_1=b_1^′−\displaystyle\sum_{j=+1}^ {a_{1j}^′ x_j }\\ \cdots\\x_=b_^′−\displaystyle\sum_{j=+1}^{a_{j}^′ x_j}\end{cases}
则
\displaystyle\begin{cases}x_1=b_1^′− {a_{1l}^′ x_l }\\ \cdots\\x_=b_^′−{a_{l}^′ x_l}\end{cases}.
因a_{l}^′≤0(=1,⋯,)，所以若{x}_l=>0，则
{x}_=b_^′−a_{l}^′ x_l≥0, (=1,⋯,)，
故\mathbf {\bar x} =(x_1,⋯,x_,0,⋯,,⋯,0)^\top仍为可行解，则
(\mathbf {\bar x})=_0+\sigma_l．
因为 \sigma_l<0，所以
(\mathbf {\bar x})=_0+\sigma_l\to−\infty ( \to +\infty)，
即线性规划的解无界．
证毕．
定理 2.3.4 （迭代解下降的判定）对非退化的基本可行解\mathbf{x}^∗=\left(\begin{matrix}\mathbf B^{−1}\mathbf b\\\mathbf 0\end{matrix}\right)，若检验数向量\mathbf \sigma的第j个分量\sigma_j<0，而向量\mathbf B^{−}\mathbf{p}_j至少有一个正分量，则可以得到一个新的基本可行解\hat{\mathbf{x}}，使得\mathbf c^\top\hat{\mathbf{x}}<\mathbf c^\top\mathbf{x}^*．
证明：令\hat{\mathbf{x}}=\mathbf{x}^∗-\theta\mathbf{\delta}，可取
\mathbf{\delta}=\begin{pmatrix}\mathbf B^{−1}\mathbf{p}_j,0,\cdots,-1,\cdots,0\end{pmatrix}，
其中
\mathbf B^{−1}\mathbf{p}_j=(_{1j}^′,_{2j}^′,⋯,_{j}^′)^\top，
记\mathbf B^{−1}\mathbf b=(_1^′,_2^′,⋯,,_^′ )^\top，要使\hat{\mathbf{x}}可行，即
\begin{split}
&\mathbf{x}^∗+\theta\mathbf{\delta}≥0 \\
⇔& \mathbf B^{−1}\mathbf b-\theta\mathbf B^{−1}\mathbf{p}_j≥0\\
⇔&\theta=\min_ \left\{\frac{_'}{_{j}'}\Big|_{j}'>0, i=1,2,\cdots,m \right\} .
\end{split}
又由于\theta>0, \sigma_j<0，且由式\displaystyle z=z_0 + \sigma_j\theta <z_0得\mathbf c^\top \hat{\mathbf{x}}<\mathbf c^\top\mathbf{x}^∗．
证毕．
由定理2.3.4及其证明，可以总结出单纯形法的选择进基变量和离基变量的一种策略．
（1）进基变量的选择：对于z=z_0+\displaystyle\sum_{j=m+1}^{n}{\sigma_j x_j}，若有两个以上的\sigma_j<0，则选最小\sigma_j对应的变量x_j入基．
（2）离基变量的选择：假设进基变量为x_j．在上一轮迭代中的多个基变量中，增大x_j最先达到0的基变量为离基变量．可以根据下式确定
l=\mathop{\text{argmin}}\limits_i \left\{\theta_i=\displaystyle\frac{b_i'}{a_{ij}'}\Big|a_{ij}'>0 \right\}，
即确定满足a_{ij}'>0且\displaystyle\frac{b_i'}{a_{ij}'}最小的i，记i=l，则选取x_l为离基变量，也称之为最小（非负）比值原则．
