刘建军

1 第一单元数学规划基础
- 1.1 序言
- 1.2 数学规划基础
2 第二单元线性规划
- 2.1 线性规划简史
- 2.2 线性规划模型
- 2.3 线性规划图解法及软件求解
- 2.4 线性规划基本定理
- 2.5 线性规划的标准形
- 2.6 标准形线性规划的解
- 2.7 单纯形法原理
- 2.8 单纯形法算法步骤及程序实现
- 2.9 表格单纯形法
- 2.10 人工变量求解线性规划问题
3 第三单元对偶规划及灵敏度分析
- 3.1 对偶规划
- 3.2 对偶单纯形法
- 3.3 灵敏度分析
- 3.4 线性规划-内点法
- 3.5 整数线性规划
4 第四单元无约束非线性优化
- 4.1 非线性优化概论
- 4.2 一维搜索算法
- 4.3 梯度类算法
  - 4.3.1 最速下降法
  - 4.3.2 牛顿法与修正牛顿法
  - 4.3.3 拟牛顿法（DFP+BFGS）
  - 4.3.4 共轭梯度法（FR）
  - 4.3.5 最小二乘法
  - 4.3.6 梯度类算法比较实验
  - 4.3.7 梯度算法历史注记
- 4.4 直接类算法
  - 4.4.1 模式搜索法（Hooke Jeeves）
  - 4.4.2 单纯形加速法
  - 4.4.3 无约束优化算法比较实验
5 第五单元约束非线性优化
- 5.1 KKT点及程序实现
- 5.2 罚函数法（SUMT）
- 5.3 可行方向法
- 5.4 二次规划（QP）
- 5.5 约束优化软件求解
6 第六单元多目标规划
- 6.1 多目标规划原理
- 6.2 多目标的四个求解技巧
- 6.3 目标规划方法
- 6.4 多目标规划应用实例
7 第七单元动态规划
- 7.1 动态规划基本概念和原理
- 7.2 动态规划应用
8 第八单元现代优化算法
- 8.1 现代优化算法概论
- 8.2 禁忌搜索算法(Taboo Search, TS)
  - 8.2.1 禁忌搜索算法原理
  - 8.2.2 禁忌搜索算法步骤与参数设置
  - 8.2.3 禁忌搜索算法的应用
- 8.3 模拟退火算法(Simulated Annealing, SA)
  - 8.3.1 模拟退火算法物理背景
  - 8.3.2 模拟退火算法步骤与数学模型
  - 8.3.3 模拟退火算法应用案例
- 8.4 遗传算法(Genetic Algrithm, GA)
  - 8.4.1 遗传算法生物学背景
  - 8.4.2 遗传算法流程用简单实例
  - 8.4.3 改进遗传算法改进与应用
- 8.5 粒子群算法(Partical Swarm Optimization， PSO)
  - 8.5.1 粒子群算法原理及实现
  - 8.5.2 粒子群算法应用实例

线性规划图解法及软件求解

1 线性规划图解法
2 内容
3 知识点检测
4 线性规划软件求解

2.3 线性规划图解法

图解法是求解线性规划问题的一种直观方法，它只适用于两个或三个变量的线性规划模型，如果是两个变量，需要绘制二维直角坐标系，如果是三个变量，则需要绘制三维坐标系．

这里只讨论两个变量的图解法，便于后面对线性规划问题的原理和几何意义进行深入理解．

2.3.1 图解法步骤

下面结合例子说明线性规划图解法的过程．

例1 用图解法求解引例模型 $max 5 x_{1} + 2 x_{2} s.t. ⎩ ⎨ ⎧ 30 x_{1} + 20 x_{2} \leq 160 5 x_{1} + x_{2} \leq 15 x_{1} \leq 4 x_{1} \geq 0, x_{2} \geq 0$ ．

解（1）画出问题的可行域，如图 2-1-1(a)；

（2）目标函数的梯度 $\nabla z = (\frac{\partial z}{\partial x _{1}}, \frac{\partial z}{\partial x _{2}})^{⊤} = (5, 2)^{⊤}$ ，如图 2-1-1(b)；

（3）任取等值线 $5 x_{1} + 2 x_{2} = c$ ，沿垂直梯度方向 $\nabla z$ 平移，求等值线将离未离可行域时与可行域的交点，如图 2-1-1(c)．

故最优解 $x^{*} = (2, 5)^{⊤}$ ，最优值 $f (x^{*}) = 20$ ，如图 2-1-1(d)．

(a)画可行域

(b)画出梯度方向

图2-1-1

线性规划图解法的4个步骤直观图

总结线性规划图解法的基本步骤如下：

（1）建立以 $x_{1}, x_{2}$ 为坐标轴的直角坐标系，画出线性规划问题的可行域；

（2）求目标函数 $z = c_{1} x_{1} + c_{2} x_{2}$ 的梯度 $\nabla z = (c_{1}, c_{2})^{⊤}$ ；

（3）任取等值线 $z_{0} = c_{1} x_{1} + c_{2} x_{2}$ ，沿梯度 $- \nabla z$ 方向平移（若是极大化问题，则沿梯度方向平移），求等值线将离未离可行域时与可行域的交点．若交点存在，则该点坐标就是最优解 $x^{*}$ ．

2.3.2 图解法的几种可能结果

（1）有唯一最优解．如例1情形．

（2）有无穷多最优解．如果例1中的目标函数变为： $max z = 10 x_{1} + 2 x_{2}$ ，则 $\nabla z = (10, 2)^{T}$ ，等值线移至中 $B$ 点时与可行域的边界线段 $A B$ 重合，如图 2-1-2‌所示．这表明线段 $A B$ 上任一点都是最优解．

图2-1-2

线性规划无穷解的情形

（3）无界解（或称无最优解）．

无界解是指线性规划问题的最优值无界．若是极大化问题，则可使目标函数值 $z \to + \infty$ ，若是极小化问题，则可使目标函数值 $z \to - \infty$ ，有无界解的线性规划问题的可行域通常是无界区域，但反之则不必然．

（4）无可行解．

某些线性规划问题的可行域是空集，既不存在满足所有约束条件的点，这时问题无可行解．在实际中出现这种情况可以认为资源条件无法满足要求，既不存在可行方案．

随堂练Python.scipy工具包

Python.scipy工具包中线性规划命令求解原料混合问题的线性规划模型

1. Matlab求解线性规划问题

matlab2003以后版本中，均提供了求解线性规划命令 linprog，针对模型为：

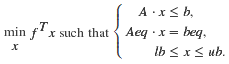
用法：

x=linprog(f,A,b,Aeq,beq,lb，...)

具体每一个变量对应意义如下：

f：目标函数的系数，也就是目标函数minZ中各个变量的系数; 当我们要求函数的最大值时，需要在linprog中写成-f；
A: 约束条件是不等式中的系数，同时在该条件下需要注意，不等号的方向不同可能我们需要对系数做一个正负变换，如果不等式为≥，那么在A中需要取原系数的相反数;
b: 不等式右边的数值，同理不等号的方向不同可能我们需要对系数做一个正负变换，如果不等式为≥，那么在b中需要取原系数的相反数;
Aeq:等式部分的系数，该题目中约束条件不存在等式，所以在函数中Aeq可以用[]来表示空白；
beq：等式等号右边的值，该问题中不存在等式，同理用[]表示；
lb：指X的下限，在我们题目中所有的变量都要求≥0，在这里lb就可以用一个0矩阵来表示，因为我们题目中有五个变量，就可以设置为lb=zeros[5,1]，就是zeros生成一个5行1列的零矩阵，通过该矩阵表示五个变量的下限。

详细参数说明，参见：https://www.mathworks.com/help/optim/ug/linprog.html.

案例：，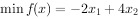

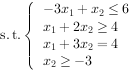
案例代码如下：

c=[-2,4]；
A=[-3 1;-1 -2];
b=[6;-4];
Aeq=[1,3]; beq=[4];
lb=[0,-3]；
[x,fval]=linprog(c,A,b,Aeq,beq,lb);
disp(x); %x为最优解
disp(fval); %fval为我们要求的最小或者最大值

简单的matlab中linprog函数应用如上，在这里可以总结给大家几点容易报错的地方：

1.写各个系数的时候，注意；和，。
2. 输入的参数顺序前后位置保持；没有的用[]填补；
3. linprog函数中用法很多，当约束条件比较多的时候，可以依次采用更复杂的形式，但是不存在的约束条件不能跳过，需要用[]表示。

2. python 求解线性规划问题

Python 的scipy包中有求解线性规划命令，即

scipy.optimize.linprog

针对模型为：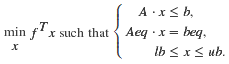

参数选择：linprog(c, A_ub, b_ub, A_ed, b_ed, bounds=None)

参数解释：

c：价值向量，只规划最小值，若规划最大值需改为-c，但注意得出的结果应再加负号即为所求最大值；
A_ub和b_ub：分别对应于不等式约束的向量，注意只取小于等于时的数组，而且A_ub必须为二维数组；
A_ed和b_ed：分别对应于等式约束的向量，取法同上；
bounds：为决策向量的上下界，例：bounds=([0, None], [None, None])表示第一个元素的取值大于等于0，第二个为实数取值。

详细参数说明，参见：https://docs.scipy.org/doc/scipy/reference/optimize.linprog-simplex.html.

案例：，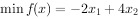

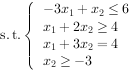
案例代码如下：

import numpy as np
from scipy.optimize import linprog
c = np.array([-2, 4])
a_ub = np.array([[-3, 1], [-1, -2]])
b_ub = np.array([6, -4])
a_ed = np.array([[1, 3]])
b_ed = np.array([4])

linprog(c, a_ub, b_ub, a_ed, b_ed, bounds=([None, None], [-3, None]))

输出如下：

con: array([0.])
fun: -38.0
message: 'Optimization terminated successfully.'
nit: 5
slack: array([48., 3.])
status: 0
success: True
x: array([13., -3.])

fun为最优解的值，x为取得最优解时对应的决策向量的取值。

3. R求解线性规划

R语言-条件约束最优化_整数规划、线性规划求解（Rglpk）。

Rglpk包中主要的函数有：

Rglpk_solve_LP((obj, mat, dir, rhs, bounds = NULL, types = NULL, max = FALSE,control = list(), ...))

其中参数：

obj规划目标系数
mat约束向量矩阵
dir约束方向向量，有’>’、’<’、’=’构成
rhs约束值
bounds上下限的约束，默认0到INF
type限定目标变量的类型,’B’指的是0-1规划,’C’代表连续,’I’代表整数，默认是’C’
control包含四个参数verbose、presolve、tm_limit、canonicalize_status。

详细参数说明，参见：https://cran.r-project.org/web/packages/lpSolve/lpSolve.pdf.

实例：

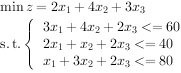
obj <- c(2, 4, 3)
mat <- matrix(c(3, 2, 1, 4, 1, 3, 2, 2, 2), nrow = 3)
# [,1] [,2] [,3]
# [1,] 3 4 2
# [2,] 2 1 2
# [3,] 1 3 2
dir <- c("<=", "<=", "<=")
rhs <- c(60, 40, 80)
max <- TRUE

Rglpk_solve_LP(obj, mat, dir, rhs, max = max)

输出结果：

$optimum
[1] 76.66667
$solution
[1] 0.000000 6.666667 16.666667
$status
[1] 0
$solution_dual
[1] -1.833333 0.000000 0.000000
$auxiliary
$auxiliary$primal
[1] 60.00000 40.00000 53.33333
$auxiliary$dual
[1] 0.8333333 0.6666667 0.0000000