PPT

多目标规划matlab求解

即含有两个或两个以上的目标函数的线性规划叫做多目标规划，现在说说几个简单的解答方法。

1.理想点法

简而言之:就是通过先求解每一个目标函数，然后将解放入评价函数里面求解

所用函数为

1. linprog(fun,x0,a,b,aeq,beq,lb,ub)

2. fmincon（fun,x0,a,b,aeq,beq,lb,ub)

列子:

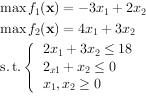
应用linprog求解第1个目标的理想点。

clc,clear

f=[3;-2];

a=[2,3;2,1];

b=[18;10];

lb=[0,0];

[x,favl]=linprog(f,a,b,[],[],lb)

求得第1个目标的理想点为

x =

    0.0000

    6.0000

favl =

  -12.0000

f=[-4;-3];

a=[2,3;2,1];

b=[18;10];

lb=[0,0];

[x,favl]=linprog(f,a,b,[],[],lb)

求得第1个目标的理想点为

x =

    3.0000

    4.0000

favl =

  -24.0000

调用fmincon求解单目标函数最优解。

clc,clear

x0=[1;1];

a=[2 3;2 1];

b=[18;10];

lb=[0;0];

ub=[];

x=fmincon('((-3*x(1)+2*x(2)-12)^2+(4*x(1)+3*x(2)-24)^2)^(1/2)',x0,a,b,[],[],lb,ub)

f1=-3*x(1)+2*x(2);

f2=4*x(1)+3*x(2);

x =

    0.5268

    5.6488

f1 =

    9.7171

f2 =

   19.0537

2、最大最小法

在决策的时候，采取保守策略是稳妥的，即在最坏的情况下，寻求最好的结果，按照此想法，可以构造如下评价函数，

φ(Z)=max z_j.

然后求解:

min q[Z(x)] = min max Z(x)

并将它的最优解x作为(3)在最大最小意义下的“最优解”。

调用 fminimax命令。

function f=mutiplesubjiect(x)

f(1)=3*x(1)-2*x(2);

f(2)=-4*x(1)-3*x(2);

clc,clear

x0=[0;0];

a=[2 3;2 1];

b=[18;10];

lb=[0;0];

[x,favl]=fminimax('mutiplesubjiect',x0,a,b,[],[],lb,[])

结果为

x =

     0

     6

favl =

   -12   -18

3、目标规划法

所用函数为: fgoalattain（fun,x0,a,b,aeq,beq,lb,ub)

goal=[12,24];

weight=[12,24];

x0=[0;0];

a=[2 3;2 1];

b=[18;10];

lb=[0;0];

[x,fval]=fgoalattain('mutiplesubjiect',goal,weight,x0,a,b,[],[],lb,[])

x=

0.0000

6.0000,

fval=  

     -12   -18

原文链接：https://blog.csdn.net/starmoth/article/details/88564081