一、整数规划实例

二、分支定界法

三、割平面法

PPT

3.4 整数线性规划

整数规划问题是运筹优化中经常遇到的一类问题，在这类问题中决策变量的类型是整数，相比于连续优化，整数规划很多时候会更难求解．在学术界整数规划一直是一个活跃的研究领域．

3.4.1 经典线性整数规划问题

整数规划的模型与线性规划基本相同，只是额外的添加了部分变量为整数的约束，其基本形式为

\begin{aligned} &\min \mathbf c^\top\mathbf x \\ &\text{s.t.} \begin{cases} \mathbf {Ax} \le \mathbf b \\ \mathbf x \in \mathbb{Z}_+^n \end{cases}. \end{aligned}

实际中的很多规划问题都能写成线性整数规划的形式，例如下面的合理下料问题．

设用某型号的圆钢下零件_1, _2,⋯,_的毛坯．在一根圆钢上下料的方式有_1, _2,⋯,_种，每种下料方式可以得到各种零件的毛坯数以及每种零件的需要量，如图 3-4-1中表格所示．问怎样安排下料方式，使得即满足需要，所用的原材料又最少？

图3-4-1每种下料方式可以得到各种零件的毛坯数以及每种零件的需要量

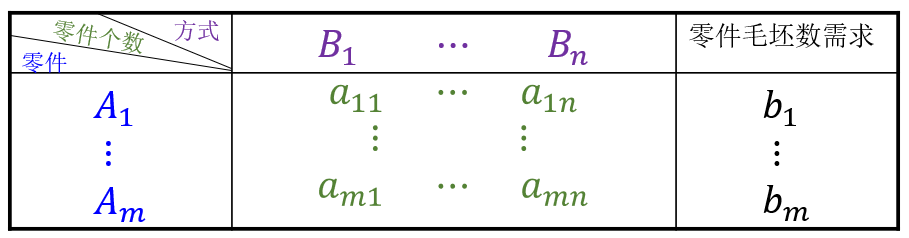
设x_j表示用B_j (=1,2,…,)种方式下料根数，那么本问题的模型可写为

\begin{aligned} &\min z=\displaystyle\sum_{=1}^ _ \\ &\text{s.t.} \begin{cases} \displaystyle\sum_{=1}^ _{} _≥_, =1,2,⋯,\\ _≥0 且为整数, j=1,2,⋯,n \end{cases}\end{aligned}．

随堂练

3.4.2 分支定界法

3.4.2.1 分支定界法原理

分支定界法（Branch and bound，BB）是求解整数规划的一种基本方法．首先去除整数约束得到“松弛模型”，使用线性规划的方法求解．

对极小化问题，若有某个变量取值\hat x且不是整数，那么在松弛模型上分别添加约束：x ≤ \lfloor \hat x \rfloor和x \ge \lceil \hat x \rceil，然后再分别求解，这个过程叫做分支．当添加约束后的模型求解结果中所有变量都是整数时，停止分支．这样不断迭代，形成了一棵树．

定界指的是分支产生叶子节点后，相当于给问题定了一个下界．之后在求解过程中只要某个节点的目标函数值大于这个下界，那就直接忽略，不用再进行分支了；每次新产生叶子节点，则更新下界．

3.4.2.2 求解步骤

下面结合例子进行说明分支定界法的过程．

例 1 求解整数规划问题

\begin{array}{l} \max\ z = 5x_1+8x_2\\ \text{s.t.}\begin{cases} 5x_1+9x_2 \leq 45\\ x_1+x_2 \leq 6\\ x_1\ge0,x_2 \ge 0均为整数 \end{cases} \tag{IP} \end{array}．二级页解

例1的求解过程可以用以下树状图（图 3-4-2）直观显示分支定界法生成树的过程．

图3-4-2分支定界法求解例1的过程树状图

Python程序：基于python 第三方工具 Gurobipy 验证本例结果

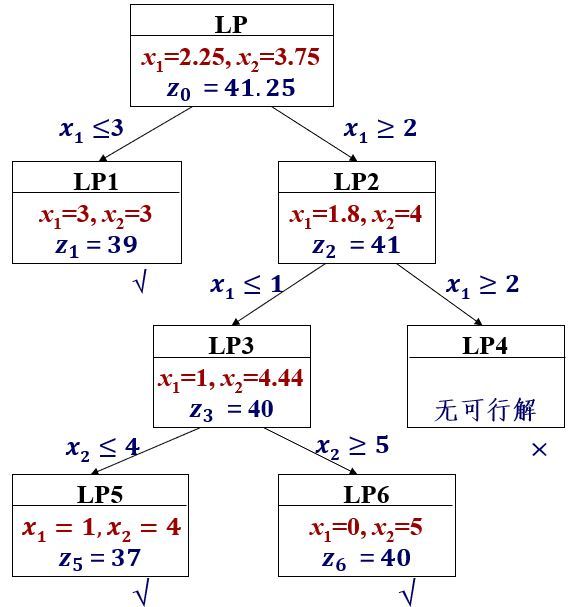
总结一下，分支定界法的一般步骤如下：

分支定界法

Step 1 初始化．从原始线性规划开始，忽略整数约束，得到一个松弛问题．求解这个松弛问题，得到一个初始解（可能包含非整数值）及其目标函数值作为当前下界．

Step 2 选择分支变量．从当前解中选择一个非整数解的变量进行分支．

Step 3 创建子问题．对选定的分支变量，创建两个子问题．在第一个子问题中，对该变量添加一个小于等于其向下取整的约束；在第二个子问题中，添加一个大于等于其向上取整的约束．这样就将原问题分解为两个更小规模的整数规划问题．

Step 4 求解子问题．分别求解这两个子问题．如果任一子问题的解是整数解，检查这个解的目标函数值．如果它优于当前已知的最佳整数解（上界），则更新最佳解．如果不是整数解，继续对非整数解的子问题进行分支．

Step 5 选择和重复．从已生成的子问题中选择一个（通常是最有希望的，比如具有最低目标函数值的LP松弛解），重复Step3和4．这个过程会形成一个搜索树，每个节点代表一个问题，分支则形成子节点．

Step 6 剪枝．在搜索过程中，如果某个子问题的LP松弛解已经劣于当前已知的最佳整数解（即上界），则可以剪掉这个子树，因为它不可能产生更好的整数解．

Step 7 终止条件．迭代进行直到找到一个整数解或所有子问题都被证明无法产生比当前最佳整数解更好的解（通过剪枝完成）．

在上述过程中，要不断应用分支、定界、估界来进行判断．当求解某子问题的松弛问题时，只要出现下列情况之一，该问题就已探明：

（1）松弛问题没有可行解，则原问题也没有可行解；

（2）松弛问题的最优解恰好全取整数，则该最优解也是其对应的子问题的最优解；

（3）松弛问题的最大值小于现有的下界，则无论其最优解是否取整数值，都将对应的子问题剪支；

已探明的子问题就不再用分支了，如果所有的子问题都已探明，则原整数规划的最优解就一定可以求出，或可以判定它无解．

分支定界法最终生成一颗树，当整数变量非常多时，求解节点会指数速度增加．

下面应用BB对例１进行求解．

## BB 求解整数规划
import numpy as np
from math import floor
from scipy.optimize import minimize ## linprog
def solution(fun, bounds, constraints):
    x_0 = []
    for i in range(len(bounds)):
        x_0.append(1)
    return minimize(fun, x_0, method='SLSQP', bounds = bounds, constraints = constraints)

def add_bounds(bounds, b_start, b_end):
    bound = [b_start, b_end]
    bounds.append(bound)

def add_constraints(constraints, type, constraint_function):
    constraint = {'type': type, 'fun': constraint_function}
    constraints.append(constraint) 
    
## Method to check if an array contains only integers
def x_is_integer(x):
    rem = 0
    for i in x:
        rem += i%1
    return rem == 0

## Method to find the index of an element with the largest decimal part in an array

def get_largest_dec_index(x):
    index = 0
    temp = 0

    for i in range(len(x)):
        r = x[i]%1
        if(r > temp):
            temp = r
            index = i
    return index

def round_array(x):
    ret = []
    for i in range(len(x)):
        ret.append(round(x[i],2))
    return ret

def floor_array(x):
    ret = []
    for i in range(len(x)):
        ret.append(floor(x[i]))
    return ret

## Method for solving maximization problems using branch and bound algorithm  

def BnB(fun, bounds, constraints):
    main_sol = solution(fun, bounds, constraints)
    x = round_array(main_sol.x)
    
    if(x_is_integer(x)):                                        ## stoping condition
        return {'x': x, 'f(x)': -fun(x)}                    ## an integer solution has been found
    UB = -fun(x)
    LB = -fun(floor_array(x))

    index = get_largest_dec_index(x)
    a = floor(x[index])
    b = a + 1
    
    ## Left branch of the recursion tree
    left_bounds = bounds.copy()
    left_bounds[index] = [left_bounds[index][0], a]
    sol1 = solution(fun, left_bounds, constraints)
    res1 = round(-sol1.fun,2) if (sol1.success or x_is_integer(sol1.x)) and (-sol1.fun <=UB and -sol1.fun >= LB) else -float('inf')  ## if potental solution is infeasble asign -infinity to it

    ## Right branch of the recursion tree
    right_bounds = bounds.copy()
    right_bounds[index] = [b, right_bounds[index][1]]
    sol2 = solution(fun, right_bounds, constraints)
    res2 = round(-sol2.fun,2) if (sol2.success or x_is_integer(sol2.x)) and (-sol2.fun <=UB and -sol2.fun >= LB) else -float('inf') ## if potental solution is infeasble asign -infinity to it


    if(res1>res2):                                                  ## deside the direction of the recursion 
        a = BnB(fun,left_bounds,constraints)                        ## find solution 
        if a["f(x)"] >= res2:                                   ## check if the soltion gives a greater result than the UB of other branch 
            return a                                                ## if yes return the solution 
        else:
            b = BnB(fun,right_bounds,constraints)                   ## get the solution for the other branch 
            return b if a["f(x)"] < b["f(x)"] else a        ## return the maximum of two solutions 

    else:
        b = BnB(fun,right_bounds,constraints)
        if b["f(x)"] >= res1:
            return b
        else:
            a = BnB(fun,left_bounds,constraints)
            return a if a["f(x)"] > b["f(x)"] else b

  ## 求解例1

obj = lambda x: -(5*x[0]+8*x[1])
h1 = lambda x: -(5*x[0]+9*x[1]-45)
h2 = lambda x: -(1*x[0]+1*x[1]-6)
bounds = []
add_bounds(bounds, 0, float('inf'))
add_bounds(bounds, 0, float('inf'))
constraints = []
add_constraints(constraints, 'ineq', h1)
add_constraints(constraints, 'ineq', h2)
print(BnB(obj,bounds, constraints))

3.4.2.3 分支定界法特点

分支定界法可应用于大量整数或混合整数优化问题（问题中决策变量可能是整数也可能不是整数）．分支定界法包含了分支和定界两个部分．分支部分将问题分解为子问题，而定界部分寻找一个松弛后的最优解，进而判断能否将某分支进行修剪．

（1）算法优点：可以求得最优解、平均速度快．因为从最小下界分支，每次算完限界后，把搜索树上当前所有的叶子结点的定界进行比较，找出定界最小的结点，此结点即为下次分支的结点．这种决策的优点是检查子问题较少，能较快的求得最佳解．

（2）算法缺点：要存储很多叶子结点的定界和对应的矩阵存储耗费．另外，分支定界方法的效率基本上由定界方法决定，若界估计不好，在极端情况下可能接近穷举搜索的计算量．

交互练习（主观题）随堂练

3.4.3 割平面法

在分支定界法中，添加的x≤\text{floor}[x]和x≥\text{ceil}[x]本质上便是在原问题中增加了超平面的约束条件，\text{floor}[x]和\text{ceil}[x]之间的整个可行域在对x进行分支的过程中被切割掉了，称为 disjunctive cuts．

割平面法由美国的 Ralph Gomory 在 19 世纪 50 年代提出，用于解决整数规划和混合整数规划问题．可以使用Gomory切割求解一个整数线性规划问题．

3.4.3.1 Gomory's cut 的思想

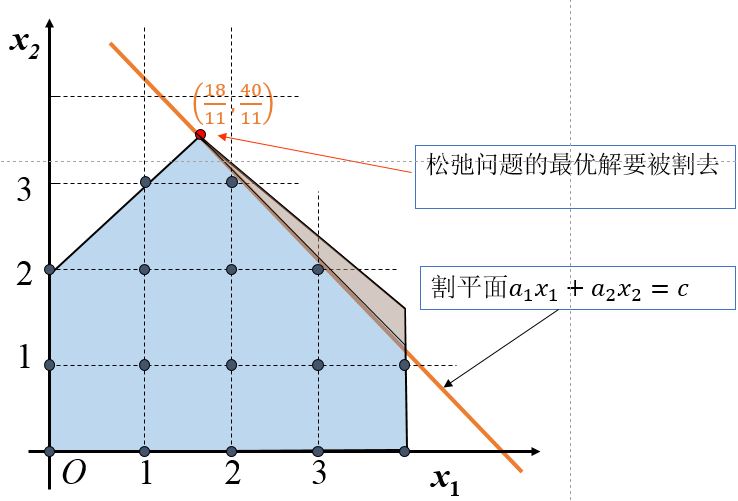
Gomory's Cut 的基本思想是添加割平面切掉LP松弛问题的非整数最优解及一部分不包含任何可行整数解的区域，通过不断缩小松弛问题的可行区域，最终达到使最优整数解成为剩余可行域极值点的目的，从而得到整数规划或者混合整数规划的最优解．图 3-4-3展示了一个2维割平面的情况．

图3-4-3割平面

对于整数集合\displaystyle\mathbf x=\left\{ \mathbf x\in \mathbb Z_{+}^{n}\left| \sum_{i=1}^n{a_ix_i}=b \right. \right\}，其中b\in \mathbb R,a_i \in \mathbb R, i=1,...,n，容易得到\mathbf x的有效不等式为

\displaystyle\lfloor b \rfloor =\lfloor \sum_{i=1}^n{a_ix_i} \rfloor \ge \sum_{i=1}^n{\lfloor a_ix_i \rfloor}\ge \sum_{i=1}^n{\lfloor a_i \rfloor x_i}（符号\lfloor ~ \rfloor表示下取整），

上式从左往右第一个等号成立是直接带入定义，第二个大于等于号成立是因为下取整符号\lfloor \cdot \rfloor的性质（即对总体下取整大于等于对每个部分下取整），第三个等号成立是因为x_i\in \mathbb Z_+，同时因为对乘积整体下取整大于对每个元素分别下取整后相乘．将上式整理可得

\displaystyle\sum_{i=1}^n{\lfloor a_i \rfloor x_i}\le \lfloor b \rfloor  ．

结合\displaystyle\sum_{i=1}^n{a_ix_i}=b可知不等式

\displaystyle\sum_{i=1}^n{\left( a_i-\lfloor a_i \rfloor \right) x_i}\ge b-\lfloor b \rfloor，

成立．

3.4.3.2 确定割平面

考虑一个线性规划问题，假设使用表格单纯形法求解后获得的不是整数解，那么选择一个非整数的变量x_i，根据松驰问题的最优单纯形表

\begin{array}{ccc|llllllll} & & & x_1& x_2&\cdots & x_m & x_{m+1}&x_{m+2} & \cdots &x_n \\ \mathbf{c_B}& \mathbf x_b &\mathbf b & c_1& c_2 & \cdots & c_m &  c_{m+1} & c_{m+2} &\cdots & c_n \\ \hline c_1 &x_1 & \bar b_1& \bar a_{11}&\bar a_{12}& \cdots& \bar a_{1m} & \bar a_{1,m+1}& \bar a_{1,m+2}&\cdots&\bar a_{1,n} \\ c_2 &x_2 & \bar b_2& \bar a_{21}&\bar a_{22}&\cdots& \bar a_{2m} & \bar a_{2,m+1}& \bar a_{2,m+2}& \cdots& \bar a_{2,n} \\ \vdots &\vdots& \vdots & \vdots & \vdots&\\c_m&x_m & \bar b_m & \bar a_{m1}& \bar a_{m2}& \cdots&\bar a_{mm} & \bar a_{m,m+1}&\bar a_{m,m+2}& \cdots& \bar a_{m,n}\\ \hline \sigma &&z & 0& 0&\cdots&0 & \sigma_{m+1}&\sigma_{m+2}&\cdots &\sigma_n \end{array}

有

x_i = \bar{b}_i -  \sum\limits_{j=m+1}^n \bar{a}_{i,j}x_j, i=1,2,\cdots,m ，\tag{1}

如果x_i不是整数，说明\bar{b}_i不一定是整数，当然\bar{a}_{i,j}也可能不是整数．将式（1）变形为

x_i + \sum\limits_{j=m+1}^n \left\lfloor \bar{a}_{i,j} \right\rfloor x_j \le \left\lfloor\bar{b}_i\right\rfloor  \tag{2},

式（1）减去式（2）得

\sum\limits_{j=m+1}^n(\bar{a_{i,j}} - \left\lfloor \bar{a_{i,j}} \right\rfloor) x_j \ge \bar{b_i} - \left\lfloor \bar{b_i} \right\rfloor\tag{3}

称式（3）为Gomory's  Cut 的源行．

下面再通过例子理解 Gomory 割平面法的过程．

例2 用割平面法求解整数规划问题\begin{array}{l}\max z=_2\\ \rm{s.t.}\begin{cases} 3_1+2_2≤6\\−3_1+2_2≤0\\_1\ge0,_2≥0 \text{且均为整数}\end{cases} \end{array}．

解：（1）求解松驰问题．

增加松弛变量s_1和s_2，得到(LP)如下的初始单纯形表

\begin{array}{ccc|ccccc} & & & x_1&x_2&s_1&s_2 \\ \mathbf{c_B}&\mathbf{x_b}&\mathbf b &0&1&0&0\\\hline 0&x_3 &6 &3&2&1&0\\ 0&x_4 &0 &-3&2&0&1\\ \hline \sigma&&z=0&0&1&0&0 \end{array}

和最优单纯形表

\begin{array}{ccc|ccccc} & & & x_1&x_2&s_1&s_2 \\ \mathbf{c_B}&\mathbf{x_b}&\mathbf b &0&1&0&0\\\hline 0&x_1 &1 &1&0&1/6&-1/6\\ 1&x_2 &3/2&0&1&1/4&1/4\\ \hline \sigma&&z=3/2&0&0&-1/4&-1/4 \end{array}

此松驰问题的最优解和最优值分别为：\mathbf x^∗=\left(x_1, x_2\right)^\top=\left(1, \frac{3}{2}\right)^\top,z= \frac{3}{2}，但x_2不是整数解．

（2）寻找割平面．

以x_2为源行生成割平面．由于

_2+ \frac{1}{4} s_1+ \frac{1}{4} s_2= \frac{3}{2} =1+  \frac{1}{2},

按割平面条件，有\frac{1}{4} s_1+\frac{1}{4} s_2≥\frac{1}{2}．若将s_1=6−3_1−2_2，s_2=3_1−2_2，带入\frac{1}{4} s_1+\frac{1}{4} s_2≥\frac{1}{2}中，得到2维割平面_2≤1，见图 1．

图1 割平面_2≤1

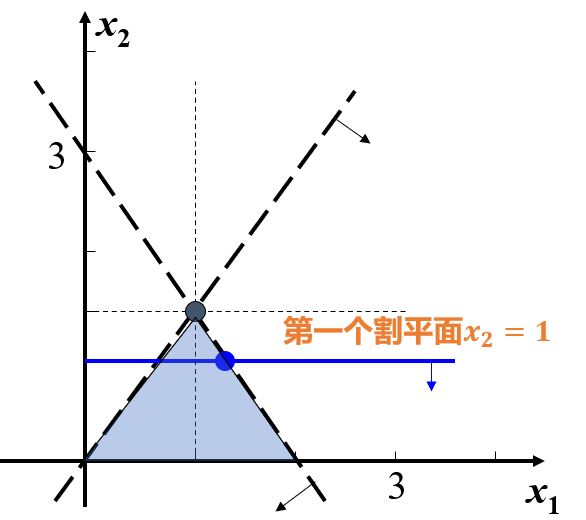
现将生成的割平面条件加入松弛变量y_1，即-\frac{1}{4} s_1-\frac{1}{4} s_2 + y_1 =-\frac{1}{2}，然后加到下表中，即

\begin{array}{ccc|ccccc} & & & x_1&x_2&s_1&s_2&y_1 \\ \mathbf{c_B}&\mathbf{x_b}&\mathbf b &0&1&0&0&0\\\hline 0&x_1 &1 &1&0&1/6&-1/6&0\\ 1&x_2 &3/2&0&1&1/4&1/4&0\\ 0&y_1 &-1/2&0&0&[\color{red}{-1/4}]&-1/4&1\\ \hline \sigma&&z=3/2&0&0&-1/4&-1/4&0 \end{array}

对上表应用对偶单纯形法，得

\begin{array}{ccc|ccccc} & & & x_1&x_2&s_1&s_2&y_1 \\ \mathbf{c_B}&\mathbf{x_b}&\mathbf b &0&1&0&0&0\\\hline 0&x_1 &2/3 &1&0&0&-1/3&2/3\\ 1&x_2 &1 &0&1&0&0&1\\ 0&s_1 &2 &0&0&1&1&-4\\ \hline \sigma&&z=1&0&0&0&0&-1 \end{array}

此时，x^{(1)}＝\left(\frac{2}{3},1\right)^\top，仍不是整数解．继续以x_1为源行生成割平面，可得新的割平面条件x_1 -\frac{1}{3}s_2+\frac{2}{3}y_1=\frac{2}{3}．

若用上表的约束解出s_2和y_1，将它们带入上式得到等价的割平面条件_1≥_2，如图2所示．

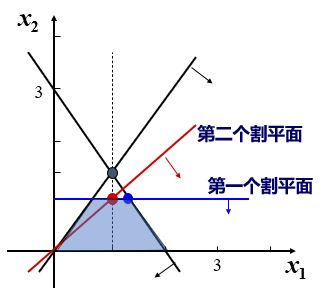
图2 割平面条件_1≥_2

再将生成的割平面条件加入松弛变量y_2，即

−\frac{2}{3}s_2−\frac{2}{3} y_1+y_2=−\frac{2}{3}，

然后加到表中，得

\begin{array}{ccc|cccccc} & & & x_1&x_2&s_1&s_2&y_1&y_2 \\ \mathbf{c_B}&\mathbf{x_b}&\mathbf b &0&1&0&0&0&0\\\hline 0&x_1 &2/3 &1&0&0&-1/3&2/3&0\\ 1&x_2 &1 &0&1&0&0&1&0\\ 0&s_1 &2 &0&0&1&1&-4&0\\ 0&y_2 &-2/3 &0&0&0&-2/3&[\color{red}{-2/3}]&1\\ \hline \sigma&&z=1&0&0&0&0&-1&0 \end{array}

根据对偶单纯形法，得

\begin{array}{ccc|cccccc} & & & x_1&x_2&s_1&s_2&y_1&y_2 \\ \mathbf{c_B}&\mathbf{x_b}&\mathbf b &0&1&0&0&0&0\\\hline 0&x_1 &0 &1&0&0&-1& 0& 1\\ 1&x_2 &0 &0&1&0&-1& 0&3/2\\ 0&s_1 &6 &0&0&1& 5&0&-6\\ 0&y_1 &1 &0&0&0&[\color{red}{1}]&1&-3/2\\ \hline \sigma&&z=0&0&0&0&1&0&-3/2 \end{array}

最后得最优单纯形表为

\begin{array}{ccc|cccccc} & & & x_1&x_2&s_1&s_2&y_1&y_2 \\ \mathbf{c_B}&\mathbf{x_b}&\mathbf b &0&1&0&0&0&0\\\hline 0&x_1 &1 &1&0&0&0& 1& -1/2\\ 1&x_2 &1 &0&1&0&0& 1& 0\\ 0&s_1 &1 &0&0&1&0&-5& 3/2\\ 0&s_2 &1 &0&0&0&1& 1&-3/2\\ \hline \sigma&&z=1&0&0&0&0&-1&0 \end{array}

所以，原问题的最优解和最优值分别为\mathbf x^∗=(1, 1)^\top ，z=1．

有以上解题过程可见，表中含有分数元素且算法过程中始终保持对偶可行性，因此，这个算法也称为分数对偶割平面算法．

3.4.3.3 Gomory 割平面法步骤及其特点

Gomory 割平面法求解整数规划的步骤如下：

（1）求解松弛问题，得到解\mathbf x^*；

（2）如果\mathbf x^*是整数解，则结束；否则转下一步；

（3）构造割平面并添加到松弛问题中，然后执行第（2）步．

割平面法也是求解整数问题的常用方法之一，但是相对于分支定界法，计算量要小许多，不用每次都要分支为两种情况进行讨论，而是用它特有的简便方法进行选择．Gomory 割平面法通过添加新的约束条件逐步逼近最优解，这种方法非常直观， 可以在不需要求解整个线性规划问题的情况下，快速地找到最优整数解；算法的复杂度比较低，可以处理中等规模的问题．但是，基本割平面法也有不足，如数值不稳定等．

随堂练

3.4.4 隐枚举法

0-1整数规划是整数规划中的特殊情形，它的变量x_{j}仅取值 0 或 1，也称二进制变量．这个条件可由下述约束条件

0\leq x_{j}\leq 1 或  x_j(x_j-1)=0

代替，这时它和一般整数规划的约束条件形式是一致的．

解0-1型整数线性规划最直观的方法，就是枚举法，即检查变量取值为0或1的每一种组合，通过比较目标函数值以求得最优解，对于含有n个变量的问题，这将需要检查变量取值的2^n个组合．对于较大的n(例如n>10)，这几乎是不可能的．因此常设计一些方法，只检查变量取值的组合的一部分，就能求到问题的最优解．这样的方法称为隐枚举法(implicit enumeration)．

可以通过以下两个途径实现隐枚举法．

1. 只要发现某个变量组合不满足其中一个约束条件时，就不必再去检验其他约束条件是否可行．

2. 若已发现一个可行解，则可根据它的目标函数值产生一个过滤条件，对于目标函数值比它差的变量组合就不必再去检验它的可行性；在以后的求解中，每当发现更好的可行解，则以此替换原来的过滤条件．

下面结合例子进行说明．

例 3 用隐枚举法求解

\begin{aligned}&\max z=3x_1-2x_2+5x_3\\ &\text{s.t}\begin{cases}x_1+2x_2-x_3\le 2 &\textcircled{1}\\ x_1+4x_2+x_3\le 4 &\textcircled{2}\\x_1+x_2\le3&\textcircled{3}\\4x_2+x_3\le 6&\textcircled{4}\\x_1,x_2,x_3=0或1\end{cases}\end{aligned}．

解 由于本问题中只有3个0,1变量，故共有2^3=8个可能解，下面进行列表操作．

\mathbf{\hat x}=(0,0,1)是一个可行解，为尽快找到最优解，可将目标函数值3 x_1－2 x_2＋5 x_3 ≥5作为一个约束（也称为过滤条件），凡是目标函数值小于5的组合不必再讨论．

表1 隐枚举法表格操作

由表 1可知，问题的最优解为\mathbf x^∗=(1, 0, 1 )．

隐枚举法在求解0-1线性整数规划时，通过智能化的选择分支和剪枝策略，避免了穷尽所有可能组合的低效做法。它在搜索过程中利用问题的结构和已经获得的信息，仅探索最有希望的解空间部分，从而在很多情况下能够更高效地找到最优解．

随堂练课外延伸利用Python工具包求解整数规划问题

一、Matlab中 intlinprog函数用法简介

1.简介

intlinprog是matlab中用于求解混合整数线性规划(Mixed-integer linear programming)的一个函数，用法基本和linprog差不多。Matlab中，该模型的标准写法如下

其中，f,x,b,beq,lb,ub,intcon是向量；A和Aeq是矩阵。

2.基本语法

x=intlinprog(f,intcon,A,b,Aeq,beq,lb,ub)

与linprog相比，多了参数intcon，代表了整数决策变量所在的位置。

例如：x1和x3是整数变量则有，intcon=[1,3]。

3.实例

求解整数规划

求解代码

f=[-5 -8];
A=[1 1;5 9];
b=[6 45];
lb=zeros(2,1);
intcon=[1 2];
[x,fval]=intlinprog(f,intcon,A,b,[],[],lb,[]);
x,
fval=-fval

所得结果为：x1=0,x2=5，z=40。

二、分支定界法python代码

目前python Scipy中没有实现线性整数规划的命令，如果实现线性整数规划的求解，需要在scipy.linprog基础上进行编程实现。

1.模型

整数规划的模型与线性规划基本相同，只是额外的添加了部分变量为整数的约束。

2. 求解步骤

整数规划求解的基本框架是分支定界法（Branchand bound，BnB）。首先去除整数约束得到“松弛模型”，使用线性规划的方法求解。若有某个变量不是整数，在松弛模型上分别添加约束：

x ≤ floor(A)

和

x ≥ ceil(A)

然后再分别求解，这个过程叫做分支。当节点求解结果中所有变量都是整数时，停止分支。这样不断迭代，形成了一棵树。
所谓的定界，指的是叶子节点产生后，相当于给问题定了一个下界。之后在求解过程中一旦某个节点的目标函数值小于这个下界，那就直接pass，不用再进行分支了；每次新产生叶子节点，则更新下界。

3. python算法实现

import math
from scipy.optimize import linprog
import sys

def integerPro(c, A, b, Aeq, beq,t=1.0E-12):
    res = linprog(c, A_ub=A, b_ub=b, A_eq=Aeq, b_eq=beq)
    if (type(res.x) is float): #produces error code
        bestX = [sys.maxsize]*len(c)
    else:
        bestX = res.x
    bestVal = sum([x*y for x,y in zip(c, bestX)])
    if all(((x-math.floor(x))<t or (math.ceil(x)-x)<t) for x in bestX):
        return (bestVal,bestX)
    else:
        ind = [i for i, x in enumerate(bestX) if (x-math.floor(x))>t and (math.ceil(x)-x)>t][0]
        newCon1 = [0]*len(A[0])
        newCon2 = [0]*len(A[0])
        newCon1[ind] = -1
        newCon2[ind] = 1
        newA1 = A.copy()
        newA2 = A.copy()
        newA1.append(newCon1)
        newA2.append(newCon2)
        newB1 = b.copy()
        newB2 = b.copy()
        newB1.append(-math.ceil(bestX[ind]))
        newB2.append(math.floor(bestX[ind]))
        r1 = integerPro(c, newA1, newB1, Aeq, beq)
        r2 = integerPro(c, newA2, newB2, Aeq, beq)
        if r1[0] < r2[0]:
            return r1
        else:
            return r2

例子：

输入

c = [3,4,1]
A = [[-1,-6,-2],[-2,0,0]]
b = [-5,-3]
Aeq = [[0,0,0]]
beq = [0]
print(integerPro(c, A, b, Aeq, beq))

输出

(8.0, array([2., 0., 2.]))

其中8是目标函数值，2，0，2是3个整数变量的值。

三、Python cplex库求解整数规划

当前使用Python求解混合整数规划问题的实例大多使用了cplex库。下面应用cplex求解0-1规划和混合整数规划和0-1整数规划

1. 混合整数规划问题

模型： 

Python代码

#导入cplex

import cplex
from cplex.exceptions import CplexError

my_obj=[3.0,1.0,3.0]#目标函数系数
my_ctype='ICI'#目标函数变量的类型，一般就是C,整数类型就是I就是integer
my_ub=[cplex.infinity, cplex.infinity,1]#变量的约束条件上限
my_lb=[0,0,0]#变量的约束条件下限
my_colnames=['x1','x2','x3']#column names列向量的名字
my_rhs=[4.0,2.0,3.0]#约束条件的值相当于b
my_rownames=['r1','r2','r3']#row names行向量的名字
#是约束条件的形式，L为小于号“less-than”,大于号是‘G’，即'greater than'
my_sense='LLL'

def populatebyrow(prob):
    #设置目标函数类型：求max or min
    prob.objective.set_sense(prob.objective.sense.maximize)
    #设置（增加）变量，明确目标函数，约束条件上限、下限，变量类型，还有变量名称
    prob.variables.add(obj=my_obj,lb=my_lb,ub=my_ub,types=my_ctype,
                      names=my_colnames)
    #对应的约束方程
    rows=[[['x1','x2','x3'],[-1.0,2.0,1.0]],
          [['x2','x3'],[4.0,-3.0]],
          [['x1','x2','x3'],[1.0,-3.0,2.0]]]
    #设置（增加）约束条件
    prob.linear_constraints.add(lin_expr=rows, senses=my_sense,
                         rhs=my_rhs,names=my_rownames)

#初始化模型
my_prob=cplex.Cplex()
#计算
handle=populatebyrow(my_prob)
#求解
my_prob.solve()
#输出结果
print(my_prob.solution.get_objective_value())
x = my_prob.solution.get_values()
print(x)

Total (root+branch&cut) =    0.03 sec. (0.01 ticks)
16.25
[4.0, 1.25, 1.0]

2. 求解0-1规划问题

例题:  某公司计划在市区的东、南、西、北四个区建立销售门市部，拟议有10个位置  可供选择， 考虑到各地居民消费水平及居民居住密集度，规定：

（1）在东区由 $A_1,A_2,A_3$ 三个点中至多选择两个；

（2）在西区由 $A_4,A_5$两个点中至少选择一个；

（3）在南区由 $A_6,A_7$两个点中至少选择一个；

（4）在北区由 $A_8,A_9，A_{10}$ 三个点中至少选择两个。

$A_j$各点的设备投资及每年可获利润由于地点不同而不同，预测情况如上表，但总投资金额不超过720万元，问应该选择哪几个销售点，可使利润最大。

解：设 0-1变量：(点被选用) 或  (点未被选用)，建立数学模型如下：

目标函数：

约束条件：

代码如下：

# utf-8
import cplex
from cplex.exceptions import CplexError

my_obj=[36.,40.,50.,22.,20.,30.,25.,48.,58.,61.]
my_ctype='IIIIIIIIII'
my_ub=[1,1,1,1,1,1,1,1,1,1]
my_lb=[0,0,0,0,0,0,0,0,0,0]
my_colnames=['x1','x2','x3','x4','x5','x6','x7','x8','x9','x10']
my_rhs=[720,2,1,1,2]
my_rownames=['r1','r2','r3','r4','r5']
my_sense='LLGGG'
def populatebyrow(prob):
    prob.objective.set_sense(prob.objective.sense.maximize)
    prob.variables.add(obj=my_obj, lb=my_lb, ub=my_ub,
                       types=my_ctype, names=my_colnames)
    rows=[[['x1','x2','x3','x4','x5','x6','x7','x8','x9','x10'],[100.0,120.0,150.0,80.0,70.0,90.0,80.0,140.0,160.0,180.0]],
          [['x1','x2','x3'],[1.0,1.0,1.0]],
          [['x4','x5'],[1.,1.]],
          [['x6','x7'],[1.,1.]],
          [['x8','x9','x10'],[1.,1.,1.]]]
    prob.linear_constraints.add(lin_expr=rows, senses=my_sense,
                         rhs=my_rhs,names=my_rownames)


my_prob=cplex.Cplex()
handle=populatebyrow(my_prob)
my_prob.solve()
print(my_prob.solution.get_objective_value())
x = my_prob.solution.get_values()
print(x)

结果：

Total (root+branch&cut) =    0.03 sec. (0.15 ticks)
245.0
[1.0, 1.0, -0.0, -0.0, 1.0, 1.0, -0.0, 0.0, 1.0, 1.0]

感兴趣同学请阅读此文：Optimizing search engines results using linear programming-2011