KKT点程序实现

实现约束优化模型    KKT点的计算。

1. python 实现

（1） 利用sympy包，实现拉格朗日乘子法的符号计算

#%% 导入sympy包，用于求导，方程组求解等等

from sympy import *  

#%% 设置变量

x1,  x2,  alpha, beta = symbols("x1  x2   alpha    beta") 

#%% 构造拉格朗日等式

L = 10 - x1*x1 - x2*x2 + alpha * (x1*x1 - x2) + beta * (x1 + x2) 

#%% 求导，构造KKT条件

dL_x1 = diff(L, x1)  #对变量x1求导

dL_x2 = diff(L, x2)  #对变量x2求导

dL_beta = diff(L, beta)  #对乘子beta求导

dualCpt = alpha * (x1 * x1 - x2)  #对偶互补条件

#%% 求解KKT等式

aa = solve([dL_x1, dL_x2, dL_beta, dualCpt], [x1, x2, alpha, beta])

#打印结果，还需验证alpha>=0和不等式约束<=0

for i in aa:

    if i[2] >= 0:

        if (i[0]**2 - i[1]) <= 0:

            print(i)

结果：

(-1, 1, 4, 6)

(0, 0, 0, 0)

（2） 利用scipy包里面的minimize函数求解

from scipy.optimize import minimize

import numpy as np  

from mpl_toolkits.mplot3d import Axes3D

from matplotlib import pyplot as plt 

 

#%% 目标函数：

def func(args):

    fun = lambda x: 10 - x[0]**2 - x[1]**2

    return fun

 

#%% 约束条件，包括等式约束和不等式约束

def con(args):

    cons = ({'type': 'ineq', 'fun': lambda x: x[1]-x[0]**2},

                 {'type': 'eq', 'fun': lambda x: x[0]+x[1]})

    return cons 

 

#%% 画三维模式图

def draw3D():

    fig = plt.figure()

    ax = Axes3D(fig)

    x_arange = np.arange(-5.0, 5.0)

    y_arange = np.arange(-5.0, 5.0)

    X, Y = np.meshgrid(x_arange, y_arange)

    Z1 = 10 - X**2 - Y**2

    Z2 = Y - X**2

    Z3 = X + Y

    plt.xlabel('x')

    plt.ylabel('y')

    ax.plot_surface(X, Y, Z1, rstride=1, cstride=1, cmap='rainbow')

    ax.plot_surface(X, Y, Z2, rstride=1, cstride=1, cmap='rainbow')

    ax.plot_surface(X, Y, Z3, rstride=1, cstride=1, cmap='rainbow')

    plt.show()

 

#%% 画等高线图

def drawContour():

    x_arange = np.linspace(-3.0, 4.0, 256)

    y_arange = np.linspace(-3.0, 4.0, 256)

    X, Y = np.meshgrid(x_arange, y_arange)

    Z1 = 10 - X**2 - Y**2

    Z2 = Y - X**2

    Z3 = X + Y

    plt.xlabel('x')

    plt.ylabel('y')

    plt.contourf(X, Y, Z1, 8, alpha=0.75, cmap='rainbow')

    plt.contourf(X, Y, Z2, 8, alpha=0.75, cmap='rainbow')

    plt.contourf(X, Y, Z3, 8, alpha=0.75, cmap='rainbow')

    C1 = plt.contour(X, Y, Z1, 8, colors='black')

    C2 = plt.contour(X, Y, Z2, 8, colors='blue')

    C3 = plt.contour(X, Y, Z3, 8, colors='red')

    plt.clabel(C1, inline=1, fontsize=10)

    plt.clabel(C2, inline=1, fontsize=10)

    plt.clabel(C3, inline=1, fontsize=10)

    plt.show()

 

#%% 程序运行 

if __name__ == "__main__":

    args = ()

    args1 = ()

    cons = con(args1)

    x0 = np.array((1.0, 2.0))  #设置初始值，初始值的设置很重要，很容易收敛到另外的极值点中，建议多试几个值

    

    #求解#

    res = minimize(func(args), x0, method='SLSQP', constraints=cons)

    #####

    print(res.fun)

    print(res.success)

    print(res.x)

 

    # draw3D()

    drawContour()

结果：

7.99999990708696

True

[-1.00000002  1.00000002]

数学优化专家 Harold W. Kuhn 小记郭科西华师范大学数学与信息学院副教授, 硕士生导师韩德仁北京航空航天大学数学科学学院教授, 博士生导师

    Harold W. Kuhn (1925年7月29日–2014年7月2日), 普林斯顿大学数学系教授, 因与他人一同创立的约束优化问题的 Karush-Kuhn-Tucker 最优性条件 (简称库恩-塔克条件) 而闻名于世. 他和诺贝尔经济学奖得主 John F. Nash 教授是研究生同学、 合作者和终身好友, Nash 教授的博士导师正是库恩-塔克条件的另一个创立者 Albert W. Tucker.

1 早期生活

    1925年7月29日, Harold W. Kuhn 出生于美国加州圣塔莫尼卡. 两年后, Kuhn 全家由圣塔莫尼卡搬到了洛杉矶中南区, 就读于那里的公立学校, 1942年高中毕业后被加州理工学院录取.

1.1 加州理工学院读大学

    Kuhn 的父亲在1939年被查出患有心脏病, 残疾保险金仅仅够家庭的生活开资. 对这样极度贫困的家庭, 能否负担起学费是一个问题. 考虑到 Kuhn 即将入学, 同时为了省钱让 Kuhn 住在家里, 他们全家搬到了加州理工学院的所在地帕萨迪纳. 1942年, Kuhn 入学并主修数学和物理. 在160个大一新生中, 尽管只有他不住在学校, 但他的成绩是最好的. 1944年7月, Kuhn 应征到美国军队服兵役并被送到罗伯茨营参加步兵基本训练. 在那里, 他通过了军队的语言能力职业检测. 基本训练完成之后被送到耶鲁大学参加日语方面的军队特别训练计划. 该计划的毕业生将最终会被送到日本去监督未来战争犯罪审讯的翻译. 1946年春天, Kuhn 做了膝盖手术, 从而放弃了日本之 行, 回学校继续念书. 1947 年, Kuhn 获得了数学学士学位. 此时, 他决定攻读博士.

1.2 选择普林斯顿大学攻读博士

    事实上, Kuhn 当时已经被耶鲁大学和普林斯顿大学同时录取. 在耶鲁大学学习日语期间, Kuhn 就旁听了代数方向的研究生课程. 另外, 他曾拜访过在普林斯顿大学的同学好友并听了少量的数学课. 他认为普林斯顿大学的数学系更强, 最终选择在那里读博士 (尽管耶鲁大学提供的奖学金更高), 从事代数和拓扑的研究.

2 攻读博士期间

2.1 遇到 Tucker 教授

    然而, 即使获得了普林斯顿大学数学系的奖学金资助, 生活仍然非常艰难, 在付完食宿费之后, 连买一双鞋的钱都没有[19]. 1948年春天, 这个“贫困的研究生”拜访了数学系的 Albert W. Tucker 教授请求暑期雇佣, 而这是他职业生涯转变的一件大事[19]. 当时 Kuhn  并不知道1948年的普林斯顿大学数学系是最好的时间和地点——遇到“对”的人并开始“对”的研究. Tucker 教授于 1905年出生于加拿大, 1928年在多伦多大学数学系大学毕业, 一年后在普林斯顿大学读博士. 1932年, 他获得了博士学位, 研究方向是拓扑学. 两年后被聘为助理教授. 1938年, Tucker 成为副教授, 1946年正式成为全职教授. 1947年10月, 线性规划单纯形方法的创始人George Dantzig 教授访问普林斯顿高等研究院并同 John von Neumann 教授讨论关于线性规划计算方面的问题. 此次会见, von Neumann 教授有了重要且富有创造力的发现, 线性规划必定存在对偶关系, 这类似于他曾在双人零和博弈中发现的线性规划和博弈模型的等价性. 此后, Dantzig 教授接连访问 von Neumann  教授, 讨论一个由高校主导的关于线性规划方面的研究项目, 并于1948年5月第一次与 Tucker 教授见面. 事实上, Tucker 教授并不熟悉 Dantzig 教授的研究领域, 当时他的任务仅仅是开车把 Dantzig 教授从普林斯顿的火车站送回华盛顿. 在回程途中, Dantzig 教授讲述了他由美国空军资助关于线性规划建模和发展单纯形法的研究项目[1]. 这些相关公开问题的重要性激起了 Tucker 教授的兴趣. 在 Dantzig 教授的鼓励下, 他立即获得了美国海军研究局提供的经费, 并于这个夏天着手研究计划. Tucker 教授选择了 Kuhn 和 David Gale (博士导师为 Tucker 教授) 两位研究生加入到研究团队. 从而, Kuhn 开始了他卓越的研究生涯.

2.2 线性规划的对偶定理

    由于对博弈论一无所知, Tucker, Kuhn 和 Gale 三人轮流讲 von Neumann 教授和 Oskar Morgenstern 教授的经典著作《博弈论和经济行为》[28]. 经过努力, 他们的研究成果给出了线性规划对偶定理以及线性规划和双人零和博弈的等价性的陈述和证明[5]. 正如 Kuhn 所说, 这个研究工作的主要结果是线性规划的对偶定理: 任何一个极小值问题总伴随着一个由相同数据构造的一个极大值问题. 如果最优解存在, 极小值与极大值相等[19]. 值得注意的是, 根据之前同 von Neumann 教授的讨论, Dantzig 教授也证明了线性规划和双人零和博弈的等价性[3]. 他们的论文于1951年发表在了同一份期刊上.

2.3 非线性规划和库恩-塔克条件的提出

    1949年秋天, Tucker 教授到斯坦福大学学术休假, 他决定继续从事最初关于线性规划与电网理论之间关系的研究. 一个很自然的问题是要研究网络中热量损耗的极小化问题, 这是一个二次规划问题(当时是一个新名词). 于是他就提议他们三人团队研究二次规划的对偶及相关问题. 然而, Gale 拒绝了这个邀请, 但 Kuhn 接受了. 这项研究工作是在斯坦福的 Tucker 教授和在普林斯顿的 Kuhn 通过写信的方式开展的 (当时还没有 Email). 根据 Kuhn 的建议, 决定研究更为一般的问题, 他们称之为非线性规划问题 (当时也是一个新名词). 他们考虑了如下问题[26]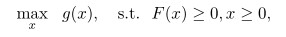：其中, x∈R^n, F(x) 是一个m维向量, 其分量f_1 (x),⋯,f_m (x)和g(x)都是x≥0时的可微实值函数. 1950年春天, 他们完成了这个问题的研究. 1950年5月, Tucker 教授在美国兰德公司的会议上报告了相关结果. 然而, Charles B. Tompkins 教授提出了一个“让人不安”的反例. 他指出 Tucker 教授和 Kuhn 的结果尽管很漂亮, 但是不能排除约束集合出现奇异的情况. Tucker 教授和 Kuhn 回去之后继续研究, 意识到约束函数的确需要满足一定的正则性条件, 从而他们就引入了所谓的约束规范 (Constraint Qualification). 1950年7月31日至8月12日, Tucker 教授应邀在第二届数学统计和概率研讨会上作报告并提交一篇论文, 他讲述了关于非线性规划的研究工作. 正是由于这个研讨会, 非线性规划这个主题进入了运筹学的理论和应用研究[17].    具有重要意义的是, 他们的结论给出了极大化非线性规划问题的解及其对偶问题解需要满足的条件. 这些条件后来被称之为库恩-塔克条件 (KT) 条件. 1939年, 芝加哥大学一位名叫 William Karush 的研究生未发表的硕士论文已经给出了类似于 KT 条件的结果[6]. 为了表达对前人的尊重，KT 条件通常又被称之为 KKT 条件. 这里有一个非常有趣的问题是，为什么 Karush 的结果不受重视且未发表? 可能的原因有两个, 一方面是 Karush 当时研究该问题的动机来源于无穷维的变分计算, 这是芝加哥学派的传统, 而 Karush 得到的结果仅仅是有限维的, 其所研究的问题和所得结果都不“重要”; 另一方面是应用数学和运筹学这些学科主要是第二次世界大战之后才开始受到重视[7].

2.4 非线性规划和库恩-塔克条件的影响

    非线性规划和 K-T 条件引领了运筹学的应用, 算法开发以及相关计算问题的快速发展. 正如 Kuhn 所说[19], 非线性规划模型可以用来描述大量日常生活中之前并没有恰当处理的问题, 运筹学在第二次世界大战中的成功运用, 一些大公司愿意尝试这个新模型; 其次, K-T 条件是众多求解非线性规划问题算法的出发点; 还有一个更为重要的原因是由于计算机的快速发展使得人们可以用程序来求解这类问题.

2.5 向量优化和多目标优化方面的影响

    Kuhn 和 Tucker 教授在论文[26]中也研究了 Tucker 教授最初打算研究的二次规划问题, 他们证明了该问题等价于一个鞍点问题. 在非常特殊的条件下, 其解集可由某线性规划问题给出. 进一步, 他们将所得结论推广到了向量极大值问题, 即对给定的线性或非线性约束, 同时极大化多个目标函数, 这里涉及到解的概念是指 Pareto 有效解. 他们的研究对向量优化问题产生了影响[2]. 同时, 他们的结果引领了多目标决策(特别是多目标线性规划)的理论研究和应用.

2.6 博士毕业

    在参与上述项目研究的同时, Kuhn 于1950年在导师 Ralph Fox 教授的指导下获得了博士学位, 研究方向是代数与拓扑. 1949年至 1950年, Kuhn 还担任数学系的教员. 此外, 1949年平安夜他还与妻子 Estelle Henkin 举行了婚礼. 这真是一段忙碌又多产的时期！

3 其它学术贡献

3.1 匈牙利算法

    1953年夏天, Kuhn 参加了在加州大学洛杉矶分校数值分析研究所举办的研讨会, 该会议的主题是讨论一系列组合优化问题, 比方说整数规划, 旅行商问题等. 在那里, 他结识了数值分析研究所的数学家 Charles B. Tompkins 教授. 当时, Tompkins 教授正在尝试求解一个分派问题: 在给定的条件下, 将n个人最优的分派到n个工作岗位. 由于10!=3628800, 对于n=10 的分派问题用数值分析研究所的计算机也无法求解, 从而他放弃了. Kuhn 那个时候正在读匈牙利数学家 Dénes König 教授于1950年写的关于图论的书[8], 他发现二分图匹配问题等价于0-1分派问题. König 教授给出了一个组合算法来求解该问题. Kuhn 决定尝试能否将该方法推广来求解一般的分派问题. 他发现 König 教授提到了匈牙利数学家 E. Egerváry 教授用匈牙利文写的一篇论文[4]. 开完会回家之后, 他买了一本匈牙利字典和语法的书试着翻译该论文. 他发现, 这篇论文里有一种方法可以将一般分派问题转化为0-1分派问题. 1953年秋天, 利用 Egerváry 教授的转化方法和 König 教授的最大匹配算法, Kuhn 成功地手算出n=12时的几个分派问题, 每个问题所花的时间不超过两个小时. 因此, 他相信结合后的算法是“好的”[21]. Kuhn 将新的算法命名为匈牙利算法, 目的是为了表达他的研究是受到两位匈牙利数学家的启发[21,23]. Kuhn 的论文[23]发表在了 Naval Research Logistics, 其影响是相当广泛的. 不久之后, 匈牙利算法被证明是多项式时间可解, 这也验证了 Kuhn 最初的猜想. 值得注意的是，2006年的时候有人发现德国数学家 Carl Jacobi (1805-1851) 对分派问题也有一定研究[27]，但他的求解方法直到去世后才用拉丁文于1890年正式发表. Kuhn 在康考迪亚大学举办的一个研讨会上对此次发现作了题为  “The Hungarian Method for the Assignment Problem and How Jacobi Beat Me by 100 Years”  的报告.

3.2 博弈论

    在博弈论方面, Kuhn 也作出了重要的贡献, 其主要贡献之一是严格地修正了 von Neumann 教授和 Morgenstern 教授的理论. 他从  von Neumann 教授和 Morgenstern 教授对n人博弈给出的两种描述：normal form (这种博弈中 Players 往往同时采取行动, 如“石头-剪子- 布”游戏) 和 extensive form (引入了时间的概念, Players 按次序采取行动, 如扑克, 象棋等)中发现[14], 尽管 normal form 相对实际, 但发现的大部分博弈都是 extensive form, 因此完善 extensive form 博弈的理论是合理的. 他对 extensive form 给出了新的博弈描述并小心翼翼地定义了一些通常在使用中容易混淆和模糊不清的概念, 比方说, 行为策略(behavior strategies) 和完美回忆(perfect recall). 他还给出了关于n人博弈解存在性的两个定理的论述, 上述研究成果发表在美国科学院院刊[14], 而这两个定理的证明单独发表于1953年[15]. 1961年, Kuhn[11]通过构造的方式给出了求解双矩阵博弈均衡策略的一种方法, 这不同于 Nash 教授 (博士导师为 Tucker 教授) 用 Kakutani 不动点定理给出的证明 (非构造性的存在性证明). 1967年, 他还研究了公平分配博弈, 将经典的两人博弈推广到了多人博弈[20]. 1969 年, Kuhn 和 George P. Szego 教授出版了一本数学在经济学中应用的书《数学系统理论与经济学》[24]. 1997年, Kuhn[13]编译了博弈论重要的早期文献, 里面的许多文献即使是在网络和数字化时代, 都很难找到.

3.3 其它方面

    定位问题是运筹和经济领域的一个重要问题, 比方说, 建立一个工厂使其到某些已知固定仓库之间的直线距离之和最短. 这个问题的历史非常悠久, 可以追溯到1643年的法国数学家 Pierre de Fermat 教授. 然而, 该问题为大众所知要归功于德国经济学家 Alfred Weber 教授. 在一系列的论文中[9,16,18], Kuhn 给出了该问题的对偶问题, 并证明了强对偶定理(对偶问题的最大值等于原始问题的最小值). 同时, Kuhn 指出该 Fermat 原始对偶问题有类似于经典的线性规划对偶的性质, 由一个问题的解可给出另一个问题的解.    除上述研究成果外，Kuhn 教授的研究还涉及线性不等式和相关系统[25], 不动点的逼近问题[12,22], 代数基本定理的构造证明[10].

4 中国之行

    1984年5月，Kuhn 教授应越民义先生之邀到中国科学院应用数学所进行访问。5月24日，越民义先生和韩继业先生陪同 Kuhn 教授及其夫人前往山东曲阜参加曲阜师范大学运筹学研究所举办的数学规划学术报告会。在此次会议上，Kuhn 教授做了三场不动点算法方面的学术报告。来自复旦大学数学系的俞文鮆教授、上海科技大学的郑权教授和山东师范大学的管梅谷教授等30多人参加了此次报告会。会后，曲阜师范大学运筹学研究所的王长钰、章志敏等陪同 Kuhn 教授夫妇参观了孔府、孔庙、孔林等景点，并游了泰山。6月8日， Kuhn 教授离开曲阜前往上海，到复旦大学进行访问。

5 荣誉与获奖

    基于 Kuhn 对运筹学理论发展所作出的贡献, 1961年被评选为计量经济学会会士; 1980年与 Tucker 教授和 Gale 教授共同获得了 von Neumann 理论奖; 1992年被评选为美国艺术与科学院院士; 1992年被匈牙利运筹学会评选为荣誉会员; 2002年被评选了运筹和管理科学学会会士; 2005 年 Naval Research Logistics 杂志评选建刊50周年最佳论文奖, 遴选委员会选择了  Kuhn 关于匈牙利算法的论文; 2009年被评选为美国工业与应用数学学会会士.致谢：感谢运筹学老前辈韩继业先生和章志敏先生提供 Kuhn 在中国的活动素材；感谢曲阜师范大学王宜举教授对本文写作的帮助。

参考文献

[1]    Albers D, Alexanderson G, Mathematical people. S. B. Maurer, interview with Albert Tucker. Birkhauser, Boston, MA, 339-348 (1985)

[2]    Cohon J, Multiobjective programming and planning. Academic, New York, NY (1978)

[3]    Dantzig G, A proof of the equivalence of the programming problem and the game problem. In: Koopmans TC (ed) Activity analysis of production and allocation. Cowles Commission Monograph 13, Wiley, New York, NY, 330-335 (1951)

[4]   Egerváry E, On combinatorial properties of matrices (trans: Kuhn H). Logistics Papers (Issue 11), Paper 4, George Washington University, Washington, DC, 1-11 (1955)

[5]    Gale D, Kuhn HW, Tucker A, Linear programming and the theory of games. In: Koopmans TC (ed) Activity analysis of production and allocation. Cowles Commission Monograph 13, Wiley, New York, NY, 317-329 (1951)

[6]    Karush W, Minima of functions of several variables with inequalities as side conditions. Master’s Thesis, Department of Mathematics, University of Chicago, Chicago, IL (1939)

[7]    Kjeldsen, TH, A contextualized historical analysis of the Kuhn-Tuck theorem in nonlinear programming: The impact of world war II. Hist Math 27: 331-361 (2000)

[8]    König D, Theorie der endlichen und unendlichen Graphen: Kombinatorische Topologie der Streckenkomplexe. Chelsea Publishing Company, New York, NY, (1950); (originally published in 1936, Mathematik in Monographien 16, Akademische Verlagsgesellschaft. Leipzig)

[9]    Kuenne R, Kuhn HW, An efficient algorithm for the numerical solution of the generalized Weber problem in spatial economics. J Reg Sci 4(2):21-33 (1962)

[10] Kuhn HW, A new proof of the fundamental theorem of algebra. Math Program Stud 1:148-158 (1974)

[11] Kuhn HW, An algorithm for equilibrium points in bimatrix games. Proc Natl Acad Sci 47(10):1657-1662 (1961)

[12] Kuhn HW, Approximate search for fixed points. In: Zadeh L, Neustadt L, Balakrishnan A (eds) Computing methods in optimization problems. Academic, New York, NY, 199-211 (1969)

[13] Kuhn HW, Classics in game theory. Princeton University Press, Princeton, NJ (1997)

[14] Kuhn HW, Extensive games. Proc Natl Acad Sci. 36(10):570-576 (1950)

[15] Kuhn HW, Extensive games and the problem of information. In: Kuhn HW, Tucker A (eds) Contributions to the theory of games, II. Annals of Mathematics Studies 28. Princeton University Press, Princeton, NJ, 193-216 (1953)

[16] Kuhn HW, Locational economics and mathematical programming. In: Proceedings of the colloquium on the application of mathematics to economics, Budapest, 1963, Publishing House of the Hungarian Academy of Sciences, 235-242 (1965)

[17] Kuhn HW, Nonlinear programming: a historical view. In: Cottle R, Lemke C (eds) Nonlinear programming: proceedings of the SIAM-AMS Symposia, New York, March, 1975, vol 9. American Mathematical Society, Providence, RI, 1-26 (1976)

[18] Kuhn HW, On a pair of dual nonlinear programs. In: Abadie J (ed) Nonlinear programming. North-Holland, Amsterdam, 38-54 (1967)

[19] Kuhn HW, On being in the right place at the right time. Oper Res 50(1):132-134 (2002)

[20] Kuhn HW, On games of fair division. In: Shubik M (ed) Essays in mathematical economics. Princeton University Press, Princeton, NJ, 29-37 (1967)

[21] Kuhn HW, On the origin of the Hungarian method. In: Lenstra J, Rinnooy Kan A, Schrijver A (eds) History of mathematical programming. North-Holland, Amsterdam, 77-81 (1991)

[22] Kuhn HW, Simplicial approximation of fixed points. Proc Natl Acad Sci 61(4):1238-1242 (1968)

[23] Kuhn HW, The Hungarian method for the assignment problem. Nav Res Logistics Q 2(1-2):83-97 (1955)

[24] Kuhn HW, Szego G, Mathematical systems theory and economics. Lecture notes in operations research and mathematical economics, Springer, New York, NY (1969)

[25] Kuhn HW, Tucker A, Linear inequalities and related systems. Annals of Mathematics Studies 38. Princeton University Press, Princeton, NJ (1956)

[26] Kuhn HW, Tucker A, Nonlinear programming. In: Neyman J (ed) Proceedings of the second Berkeley symposium on mathematical statistics and probability, University of California Press, Berkeley, CA, 481-492 (1951)

[27] Ollivier F, Sadik B, La borne de Jacobi pour une diffiete’ definie par un systeme quasi regulier. Comptes Rendus de l’Academie des Sciences de Paris. 345(3):139-144 (2007)

[28] von Neumann J, Morgenstern O, The Theory of Games and Economic Behavior. Princeton University Press, Princeton, NJ (1944)