刘建军

1 第一单元数学规划基础
- 1.1 序言
- 1.2 数学规划基础
2 第二单元线性规划
- 2.1 线性规划简史
- 2.2 线性规划模型
- 2.3 线性规划图解法及软件求解
- 2.4 线性规划基本定理
- 2.5 线性规划的标准形
- 2.6 标准形线性规划的解
- 2.7 单纯形法原理
- 2.8 单纯形法算法步骤及程序实现
- 2.9 表格单纯形法
- 2.10 人工变量求解线性规划问题
3 第三单元对偶规划及灵敏度分析
- 3.1 对偶规划
- 3.2 对偶单纯形法
- 3.3 灵敏度分析
- 3.4 线性规划-内点法
- 3.5 整数线性规划
4 第四单元无约束非线性优化
- 4.1 非线性优化概论
- 4.2 一维搜索算法
- 4.3 梯度类算法
  - 4.3.1 最速下降法
  - 4.3.2 牛顿法与修正牛顿法
  - 4.3.3 拟牛顿法（DFP+BFGS）
  - 4.3.4 共轭梯度法（FR）
  - 4.3.5 最小二乘法
  - 4.3.6 梯度类算法比较实验
  - 4.3.7 梯度算法历史注记
- 4.4 直接类算法
  - 4.4.1 模式搜索法（Hooke Jeeves）
  - 4.4.2 单纯形加速法
  - 4.4.3 无约束优化算法比较实验
5 第五单元约束非线性优化
- 5.1 KKT点及程序实现
- 5.2 罚函数法（SUMT）
- 5.3 可行方向法
- 5.4 二次规划（QP）
- 5.5 约束优化软件求解
6 第六单元多目标规划
- 6.1 多目标规划原理
- 6.2 多目标的四个求解技巧
- 6.3 目标规划方法
- 6.4 多目标规划应用实例
7 第七单元动态规划
- 7.1 动态规划基本概念和原理
- 7.2 动态规划应用
8 第八单元现代优化算法
- 8.1 现代优化算法概论
- 8.2 禁忌搜索算法(Taboo Search, TS)
  - 8.2.1 禁忌搜索算法原理
  - 8.2.2 禁忌搜索算法步骤与参数设置
  - 8.2.3 禁忌搜索算法的应用
- 8.3 模拟退火算法(Simulated Annealing, SA)
  - 8.3.1 模拟退火算法物理背景
  - 8.3.2 模拟退火算法步骤与数学模型
  - 8.3.3 模拟退火算法应用案例
- 8.4 遗传算法(Genetic Algrithm, GA)
  - 8.4.1 遗传算法生物学背景
  - 8.4.2 遗传算法流程用简单实例
  - 8.4.3 改进遗传算法改进与应用
- 8.5 粒子群算法(Partical Swarm Optimization， PSO)
  - 8.5.1 粒子群算法原理及实现
  - 8.5.2 粒子群算法应用实例

对偶规划

1 视频与课件
2 内容
3 知识点检测
4 历史注记
5 知识扩展

二、线性规划标准形式的对偶

三、线性规划对偶的6个定理

PPT

对偶（dual）理论是在1947年由美籍匈牙利数学家

冯·诺依曼‌

提出创立．线性规划对偶理论是研究线性规划中原始问题与对偶问题之间关系的理论，对偶问题是线性规划早期发展中最重要的发现，即对一个线性规划问题（称为原始问题，简记为LP），均存在一个与它对应的对偶线性规划问题（称为对偶问题，简记为DP）．在原始问题和和对偶问题中求解任何一个问题时，会同时得到另一个问题的最优解；当对偶问题比原始问题有较少约束时，求解对偶规划比求解原始规划更方便．

3.1.1 线性规划对偶问题

先考虑一个实际生产计划优化问题．

引例（生产计划优化问题）某厂生产A、B、C三种产品，三种产品的单位利润分别为12、18和15、资源消耗如表 3-1-1，求总利润最大的生产方案．

表3-1-1生产计划信息

	A	B	C	资源限制
原料1/单位产品	6	9	5	200
原料2/单位产品	12	16	17	360
人工/单位产品	25	20	12	780
产品单位利润	12	18	15

设生产A、B、C分别为 $x_1$ 、 $x_2$ 、 $x_3$ 个单位，则可以建立线性规划模型

$\begin{aligned} &\max z = 12{x_1} + 18{x_2} + 15{x_3}\\ &\text{s.t.}\begin{cases} 6{x_1} + 9{x_2} + 5{x_3} \le 200\\ 12{x_1} + 16{x_2} + 17{x_3} \le 360\\ 25{x_1} + 20{x_2} + 12{x_3} \le 780\\ {x_i} \ge 0,\ i=1,2,3 \end{cases} \end{aligned}.$

如果厂家不想自己生产产品，而是将企业的三种资源（原料1、原料2和人工）出租给第三方．设单位资源 $i$ 租金为 $y_i，i = 1,2,3$ ，则6个单位资源1、12个单位资源2、25个人工相当于一个单位产品A，故这些资源的总租价应至少为产品A的售价，否则出租不如自己生产产品A．即

$6y_1 + 12y_2 + 25y_3 \geq 12$ ．

同理有

$9y_1 + 16y_2 + 20y_3 ≥ 18，\\5y1 + 17y_2 + 12y_3 ≥ 15．$

于是可得到如下的对偶规划问题

$\begin{aligned} &\min w = 200{y_1} + 360{y_2} + 780{y_3}\\ &\text{s.t.}\begin{cases} 6{y_1} + 12{y_2} + 25{y_3} \ge 12\\ 9{y_1} + 16{y_2} + 20{y_3} \ge 18\\ 5{y_1} + 17{y_2} + 12{y_3} \ge 15 \\ {y_1} \ge 0,{y_2} \ge 0,{y_3} \ge 0 \end{cases}\end{aligned}.$

通过表格单纯形法可得，此对偶问题的最优目标值与原始问题的最优目标值相等， $z=w=402.7397$ ．

Python 程序应用 scipy 优化工具求引例及其对偶最优解

3.1.2 对偶线性规划问题推导

3.1.2.1 一般形式的线性规划问题

给定一个一般的线性规划问题

\begin{split}&\min z=\mathbf c^\top\mathbf x\\ &\text{ s.t.}\begin{cases} \mathbf A\mathbf x \ge \mathbf b\\ \mathbf x \ge\mathbf 0\end{cases}\tag{LP} \end{split}

其中 $\mathbf A\in \mathbb R^{m\times n}$ 为行满秩矩阵， $\mathbf x\in \mathbb R^n$ ．引入非负松弛变量 $\mathbf x_s\in \mathbb R^m$ ，将 LP 问题标准化，得

\begin{split}&\min z=\mathbf c^\top\mathbf x +\mathbf 0 \mathbf x_s\\&\text{s.t.}\begin{cases}\mathbf A\mathbf x - \mathbf I_m\mathbf x_s = \mathbf b,(\mathbf I_m为单位阵)\\\mathbf x \ge 0,\mathbf x_s\ge 0\end{cases}\end{split}．

不妨假设 $(\mathbf A,-\mathbf I)$ 可表示为 $(\mathbf B, \mathbf N)$ ，则线性规划问题可改写为

\begin{split} &\min z=\mathbf c_\mathbf{B}^\top\mathbf {x_B} +\mathbf c^\top_{\mathbf N} \mathbf {x_N}\\&\text{s.t.}\begin{cases}\mathbf {Bx_B} + \mathbf{Nx_N} = \mathbf b\\\mathbf {x_B} \ge 0,\mathbf {x_N}\ge 0\end{cases}\end{split}

可得基本可行解 $\mathbf{x} =\begin{pmatrix}\mathbf B^{-1}\mathbf b\\ \mathbf 0\end{pmatrix}$ ，目标函数值 $z=\mathbf c^\top_{\mathbf B}\mathbf B^{-1}\mathbf b$ ．

若记 $\mathbf y^\top=\mathbf c^\top_{\mathbf B}\mathbf B^{-1}$ ，等号两边同右乘 $\mathbf b$ ，则

\mathbf y^\top\mathbf b = \mathbf c^\top_{\mathbf B}\mathbf B^{-1}\mathbf b = z.\tag{3.1.1}

当非基变量检验向量 $\boldsymbol{\sigma_N}=\mathbf c_\mathbf {N}^\top-\mathbf y^\top\mathbf N≥\mathbf 0$ 时，则 $\mathbf {x}=\begin{pmatrix}\mathbf B^{-1}\mathbf b\\ \mathbf 0\end{pmatrix}$ 为最优解．又因为基变量检验数 $\boldsymbol\sigma_B=\mathbf c^\top_{\mathbf B} -\mathbf y^\top\mathbf B=$ ，所以

\begin{split}&(\mathbf{\sigma_B},\mathbf{\sigma_N})= (\mathbf c_{\mathbf B}, \mathbf {c_N})^\top-\mathbf y^\top(\mathbf B,\mathbf N)\ge \\ \Rightarrow &(\mathbf c^\top, \mathbf 0)-\mathbf y^\top(\mathbf A,-\mathbf I)\ge \end{split},

即

\mathbf y^\top\mathbf A\le \mathbf c^\top,\quad \mathbf y^\top\ge ,\tag{3.1.2}

且称 $\mathbf y^\top=\mathbf c^\top_{\mathbf B}\mathbf B^{-1}$ 为单纯形乘子．

因此，由式（3.1.1）和（3.1.2）可得

$\mathbf {y}^\top \mathbf{A} \le \mathbf c^\top \Leftrightarrow \mathbf {A}^\top \mathbf{y} \le \mathbf c$ ，

$\mathbf y^\top \ge \mathbf 0$ ，

$\mathbf y^\top\mathbf b = \mathbf c^\top_{\mathbf B}\mathbf B^{-1}\mathbf b$ ，

且由 $\mathbf{Ax} \ge \mathbf b,\mathbf y^\top≥$ 可得 $\mathbf {y}^\top \mathbf{A}\mathbf x≥\mathbf y^\top\mathbf b$ ，故 $\mathbf {y}^\top \mathbf b$ 只存在最大值．所以，可以得到原线性规划LP的对偶线性规划DP，即

\begin{split} &\max \ \ \mathbf b^\top\mathbf y \\ &{\rm s.t.} \begin{cases} \mathbf{A}^\top\mathbf{y}\le \mathbf c\\ \mathbf y\ge\mathbf 0 \end{cases} \end{split}\tag{DP}.

3.1.2.2 标准形式的线性规划问题

给定一个标准形式的线性规划问题

$\begin{aligned} &\min z=\mathbf c^\top\mathbf x\\ &{\rm s.t.} \begin{cases} \mathbf{Ax} ＝ \mathbf b\\ \mathbf x \ge 0 \end{cases} \end{aligned}$ ，

由于任何一个等式约束都可以用两个不等式约束等价地表示，所以

$\begin{aligned} &\min z=\mathbf c^\top\mathbf x\\ &{\rm s.t.} \begin{cases} \begin{pmatrix}\mathbf A\\-\mathbf A\end{pmatrix}\mathbf x \ge \begin{pmatrix}\mathbf b\\-\mathbf b\end{pmatrix}\\ \mathbf x \ge 0 \end{cases} \end{aligned}$ ，

则它的对偶规划为

$\begin{aligned} &\max w=(\mathbf y_1,\mathbf y_2)\begin{pmatrix}\mathbf b\\-\mathbf b\end{pmatrix}=(\mathbf y_1-\mathbf y_2) \mathbf b\\ &{\rm s.t.} \begin{cases} (\mathbf y_1,\mathbf y_2)\begin{pmatrix}\mathbf A\\-\mathbf A\end{pmatrix}=(\mathbf y_1,\mathbf y_2)\mathbf A \le \mathbf c \\ \mathbf y_1\ge 0,\mathbf y_2 \ge 0 \end{cases} \end{aligned}$ ．

若令 $\mathbf y=\mathbf y_1-\mathbf y_2$ ，显然 $\mathbf y$ 没有符号限制，则线性规划标准形的对偶规划为

$\begin{aligned} &\max \ w= \mathbf y \mathbf b\\ &{\rm s.t.} \begin{cases} \mathbf {yA}\le \mathbf c\\ \mathbf y\text{无约束} \end{cases} \end{aligned}$ ．

例1 写出下列线性规划的对偶问题 $\begin{aligned} &\max z=5x_1+4x_2+6x_3 \\ &{\rm s.t.} \begin{cases} x_1 +2x_2\ge 2\\ x_1 +x_3≤3\\ −3x_1+2x_2+x_3≤−5\\ x_1−x_2+x_3 =1\\ x_1≥0,x_2≤0,x_3\text{无约束} \end{cases} \end{aligned}$ ．

解由原问题可得 $\mathbf c=(5,4,6)^\top$ ， $\mathbf A=\begin{pmatrix}1&2&0\\1&0&1\\-3&2&1\\1&-1&1\end{pmatrix}$ ， $\mathbf b=(2,3,-5,1)^\top$ ．原问题目标为最大化，所以，

$x_1\geq0$ 对应的约束为 $y_1 + y_2-3y_3 +y_4\geq5$ ，

$x_2\leq0$ 对应的约束为 $2y_1 +2y_3 -y_4\leq4$ ，

$x_3$ 对应的约束为 $y_2 +y_3 +y_4=6$ ．

故其对偶规划为 $\begin{aligned} &\min w=2y_1+3y_2−5y_3 +y_4 \\ &{\rm s.t.} \begin{cases} y_1 + y_2−3y_3 +y_4≥5\\ 2y_1 +2y_3 −y_4≤4\\ y_2 +y_3 +y_4=6\\ y_1≤0,y_2≥0,y_3≥0,y_4\text{无约束}． \end{cases} \end{aligned}$

下面的表 3-1-2列出了线性规划与其对偶的对应关系．

表3-1-2线性规划对偶格式

目标函数 max	对偶目标函数 min
变量数： $m$ 个	约束条件： $m$ 个
第 $i$ 个变量 $x_i\ge0$	第 $i$ 个约束类型为 “ $\geq$ ”
第 $i$ 个变量 $x_i\leq0$	第 $i$ 个约束类型为 “ $\leq$ ”
第 $i$ 个变量无约束	第 $i$ 个约束类型为“ $＝$ ”
约束条件： $n$ 个	变量数： $n$ 个
第 $j$ 个约束类型为“ $\geq$ ”	第 $j$ 个变量 $x_j\leq 0$
第 $j$ 个约束类型为“ $\leq$ ”	第 $j$ 个变量 $x_j\ge 0$
第 $j$ 个约束类型为“ $=$ ”	第 $j$ 个变量无约束

3.1.2.3 对偶的几何解释

对偶问题的几何结构本质上与原问题完全相同，因为二者都是线性规划问题，因此其可行域都是多面体集合，下面的特殊例子具有较直观的几何效果．考虑问题

$\begin{aligned}&\max 6x_1 + 6x_2\\&\text{s.t.}\begin{cases}3x_1 + 2x_2 \le 6\\ 2x_1 + 3x_2 \le 6\\ x_1\ge0, x_2\ge 0\end{cases}\end{aligned}$ ，

易知 $\mathbf A =\begin{pmatrix}3& 2\\ 2& 3\end{pmatrix}$ ， $\mathbf c =(6,6)$ ， $\mathbf b =\begin{pmatrix}6\\ 6\end{pmatrix}$ ．注意到矩阵 $\mathbf A$ 是对称矩阵，并且 $\mathbf c^\top =\mathbf b$ ，所以对偶问题为

$\begin{aligned}&\min 6y_1 + 6y_2\\&\text{s.t.}\begin{cases}3y_1 + 2y_2 \ge 6\\ 2y_1 + 3y_2 \ge 6\\ y_1\ge0, y_2\ge 0\end{cases}\end{aligned}$ ．

从几何直观上看，对偶问题的可行域是原问题可行域的镜像（忽略非负性约束）．这一点在图 3-1-1中得到了直观体现．

图3-1-1特定情况下，原问题和对偶问题的几何形状通过某种反射操作互为镜像关系

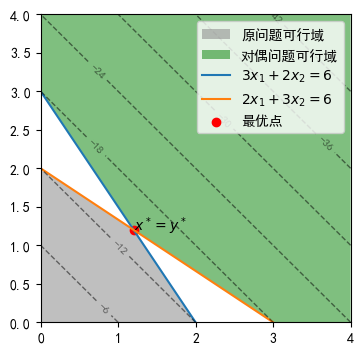
如图 3-1-1所示，当 $\mathbf c^\top =\mathbf b$ ，且 $\mathbf A$ 为对称矩阵时，在这种特定情况下，原问题和对偶问题的几何形状通过某种反射操作互为镜像关系，直观上表现为它们各自的可行域在不考虑变量非负约束时呈现出对称特点．

也可以使用单纯形法来演示解决该问题的过程．首先，将原问转化为标准形式

$\begin{aligned}&\min z= -6x_1 -6x_2\\&\text{s.t.}\begin{cases}3x_1 + 2x_2 +x_3 = 6\\ 2x_1 + 3x_2 +x_4 = 6\\ x_i\ge0, i=1,2,3,4\end{cases}\end{aligned}$ ，

那么初始单纯形表为

\begin{array}{ccc|cccc|c} & & & x_1&x_2&x_3&x_4& & \\ \mathbf{c_B}&\mathbf{x_b}&\mathbf b & -6 &-6& 0&0 & \theta_i= \frac{b_i}{a_{ij}}\\ \hline 0 &x_3 & 6 & \color{red}{[3}] & 2 & 1 & 0&2 \\ 0 &x_4 & 6 & 2&3 & 0 &1 & 2 \\ \hline &\sigma && -6& -6 & 0 & 0 \end{array}

因为初始 $\mathbf {c_B} = (0, 0)^\top$ ，因此单纯形乘子 $\mathbf y =\mathbf{c_B}\mathbf B^{-1} = (0, 0)^\top$ ．这意味着在单纯形法开始时， $y_1 = 0，y_2= 0，x_1 = 0，x_2 = 0$ ， $z=0$ ．所以从原点开始，而原点位于原问题的可行域内但不在对偶问题的可行域内．如果选择 $x_1$ 作为进基变量进行迭代，则更新后得到的单纯形表为

\begin{array}{ccc|cccc|c} & & & x_1&x_2&x_3&x_4& & \\ \mathbf{c_B}&\mathbf{x_b}&\mathbf b & -6 &-6& 0&0 & \theta_i= \frac{b_i}{a_{ij}}\\ \hline -6 &x_1 & 2 & 1 & 2/3 & 1/3 & 0&3 \\ 0 &x_4 & 2 & 0&\color{red}{[5/3]} & -2/3 &1 & 6/5 \\ \hline &\sigma && 0& -2 & 2 & 0 \end{array}

此时注意到 $x_1 = 2，x_2 = 0，y_1 = 2，y_2 = 0$ ， $z=-12$ ．这个点对于原问题是可行的，但对于对偶问题仍然是不可行的．这一过程在图 3-1-2附录 / 附录程序‌中有展示．

2.5 dual2d2

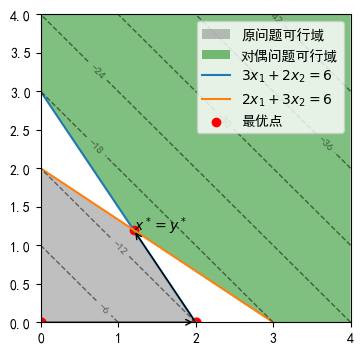
单纯形算法从原问题可行区域内的一个可行点开始．在这个例子中，这也是对偶问题的一个起始点，不过该点在对偶问题中是不可行的．单纯形算法通过原问题的可行区域逐步向对偶问题可行区域内的某一点移动．当算法结束时，算法会到达那个同时位于原问题与对偶问题可行区域内的唯一点．

图3-1-2

单纯形法求解原问题（原点为初始迭代点）

再以 $x_2$ 为进基变量时，得到最优的单纯形表

$\text{[math]}$

在这个最优点上， $x_1 = x_2 = y_1 = y_2 = \frac{6}{5}$ ， $-z=\frac{72}{5}$ ，这对于原问题和对偶问题都是可行的．这个步骤同样在图 3-1-2中有展示．需要注意的是，这个问题是非典型性的，因为它原问题和对偶问题的可行域共享一个公共点．在更标准的问题中，通常无法如此方便地绘制出两个可行域，但单纯形过程是相同的．单纯形算法起始于原问题可行域内的一个点，对应的对偶向量 $\mathbf y$ 并不在对偶问题的可行域内．随着单纯形算法的推进，对偶向量 $\mathbf y$ 逐渐接近并最终进入对偶问题的可行域．

随堂练随堂练

3.1.3 对偶线性规划的性质

根据对偶的定义，可以得到定理3.1.1．

定理3.1.1 对偶问题的对偶是原问题．

定理3.1.2（弱对偶定理）设 $\mathbf x$ 是原始规划 LP 的可行解， ${\mathbf y}$ 是对偶规划 DP 的可行解，则恒有 $\mathbf c^\top\mathbf x\le \mathbf b^\top\mathbf y.$

证明：因为 $\mathbf y$ 是对偶问题的可行解，所以满足约束条件

$\mathbf y≥0 , \mathbf A^\top\mathbf y≤\mathbf c;$

因为 $\mathbf x$ 是原问题的可行解，可得 $\mathbf x≥0 ，\mathbf A\mathbf x≥\mathbf b$ ，所以

$\mathbf c^\top\mathbf x\le (\mathbf A^\top\mathbf y)^\top\mathbf x=\mathbf y^\top(\mathbf A\mathbf x)\le \mathbf y^\top\mathbf b=\mathbf b^\top\mathbf y.$

证毕．

由弱对偶定理，可得如下结论：

结论1：对偶问题中，任意一个可行解，都产生了另一个问题的目标函数的界．

结论2：若互为对偶问题中任意一个有可行解，但无最优解，则另一个就无可行解．

因为原问题与对偶问题互为对偶，由定理3.1.2直接得到以下定理．

定理3.1.3（最优性定理）如果 $\mathbf x$ 和 $\mathbf y$ 分别是原始规划和对偶规划的可行解，且 $\mathbf c^\top\mathbf x=\mathbf b^\top\mathbf y$ ，则 $\mathbf x,\mathbf y$ 分别是它们的最优解．

定理3.1.4（强对偶定理）如果原始规划有最优解，则对偶规划也有最优解，且它们最优值相等，反之亦然．

证明：充分性．先引入松弛变量 $\mathbf x_s$ ，将 LP 写成

\begin{split} &\min \ \ \mathbf c^\top\mathbf x\\ &{\rm s.t.}\begin{cases} \mathbf{Ax} - \mathbf I_m\mathbf{x}_s =\mathbf b\\ \mathbf x\ge\mathbf 0,\mathbf x_s \ge\mathbf 0 \end{cases}. \end{split}

设最优解的基为 $\mathbf B$ ，则基变量 $\mathbf{x_B}=\mathbf B^{-1}\mathbf b$ ，检验数 $\boldsymbol\sigma\ge \mathbf 0$ ，其中 $\boldsymbol\sigma$ 分为两部分，对应 $\mathbf x$ 的 $\mathbf\sigma_1$ 和对应 $\mathbf{x}_s$ 的 $\mathbf\sigma_2$ ，即

\sigma_1^\top=\mathbf c^\top-\mathbf{c}_\mathbf{B}^\top\mathbf B^{-1}\mathbf A\ge0, \qquad\sigma_2^\top = \mathbf {c}_\mathbf{B}^\top\mathbf B^{-1}\mathbf I = \mathbf {c}_\mathbf{B}^\top\mathbf B^{-1}\ge0.

令 ${\mathbf y}^\top=\mathbf {c}_\mathbf{B}^\top\mathbf B^{-1}$ ，则有 ${\mathbf y}\ge \mathbf 0$ ，且 $\mathbf A^\top{\mathbf y}\le \mathbf c$ ，从而 $\mathbf y$ 是 DP 的可行解，又因为 $w=\mathbf b^\top{\mathbf y}={\mathbf y}^\top\mathbf b=\mathbf {c}_\mathbf{B}^\top\mathbf B^{-1}\mathbf b=\mathbf {c}_\mathbf{B}^\top \mathbf x= z,$ 从而 $\mathbf y$ 是 DP 的最优解.充分性得证．

必要性．因为对偶规划的对偶问题是原始规划，由上述充分性可直接得出必要性．

证毕．

定理3.1.5（互补松弛条件）若 $\bar{\mathbf x}$ 和 $\bar{\mathbf y}$ 分别是原问题 LP 问题和对偶问题 DP 的可行解，这两个解为各自都是对应问题的最优解的充要条件是

\begin{cases} \bar{\mathbf y}^\top \mathbf {x}_s= \mathbf 0 \\ \mathbf {y}_s\bar{\mathbf x}^\top= \mathbf 0 \end{cases}\tag{3.1.3}，

其中 $\mathbf{y}_s , \mathbf{x}_s$ 分别是对偶问题的松弛变量和原问题的剩余变量．

证明：对原问题 LP 和对偶问题 DP 分别引入剩余变量 $\mathbf{x}_s$ 和松弛变量 $\mathbf{y}_s$ ，则

- 将原问题的约束方程变为等式， $\mathbf A \mathbf{x}-\mathbf{x}_s = \mathbf b$ ，其中 $\mathbf{x}_s\ge 0$ ；

- 将对偶问题的约束方程变为等式， $\mathbf A^\top \mathbf{y}+ \mathbf{y}_s=\mathbf c$ ，其中 $\mathbf{y}_s\ge 0$ ．

因为 $\bar{\mathbf x}$ 、 $\bar{\mathbf y}$ 分别是原问题 LP 问题和对偶问题 DP 的最优解，根据强对偶定理，得

\mathbf c^\top\bar{\mathbf x}=\mathbf b^\top\bar{\mathbf y}，

将 $\mathbf A \mathbf{x}-\mathbf{x}_s = \mathbf b$ 、 $\mathbf A^\top \mathbf{y}+ \mathbf{y}_s=\mathbf c$ 两端分别左乘、右乘 $\bar{\mathbf y}^\top$ 、 $\bar{\mathbf x}^\top$ ，然后相减，得到

\bar{\mathbf y}^\top\mathbf{x}_s+\mathbf{y}_s\bar{\mathbf x}^\top=\mathbf{c}^\top\bar{\mathbf x}-\bar{\mathbf y}^\top\mathbf{b}=0

其中 $\bar{\mathbf y}$ 、 $\mathbf{x}_s$ 、 $\mathbf{y}_s$ 、 $\bar{\mathbf x}$ 都是大于等于 0，所以等号两边的值都是 0，即

\begin{cases}\bar{\mathbf y}^\top \mathbf{x}_s= 0 \\ \mathbf{y}_s\bar{\mathbf x}^\top= 0 \end{cases}.

即若令 $\bar{\mathbf y}=(_1,_2,⋯,_ )^\top, \bar{\mathbf x}_=(_{+1},_{+2},⋯,_{+})^\top$ ，则

_=0~ 或 ~_{+}=0， =1,⋯,.

若令 $\bar{\mathbf y}_= (_{+1},_{+2},⋯,_{+} )^\top, \bar{\mathbf x}=(_1,_2 ,⋯,_ )^\top$ , 则

_=0 ~或~ _{+}=0，=1,⋯,.

反之亦然．

证毕．

2.5dualrelex

图3-1-3互补松弛条件直观图

图 3-1-3直观展示了定理3.1.5的结论，即 $x_j y_{m+j}=0(i=1,2,…,m)$ ， $y_i x_{n+i}=0$ $(j=1,2,\dots,n)$ ，也就是说，在每对变量中，其中一个大于0，另一个一定等于0．

例2 已知线性规划问题 $\max⁡ =4_1+3_2\\\text{s.t.}\begin{cases}_1+2_2≤2\\_1−_2≤3\\2_1+3_2≤5\\_1 +_2≤2\\3_1+_2≤3\\_i\ge 0, i=1,2\end{cases}$ ，其对偶问题的最优解 $\mathbf y=(1,0,0,0,1)^\top$ ，最优值 $w_{\min}=5$ ．试用互补松弛定理找出原问题的最优解．

解原问题的对偶问题为

$\min ⁡=2y_1+3y_2+5_3+2y_4+3y_5\\\text{s.t.}\begin{cases}y_1+y_2+2y_3+y_4+3y_5≥4\\2y_1 −y_2+3y_3+y_4+y_5≥3\\y_i≥0, =1,2,3,4,5\end{cases}$ ，

由对偶问题最优解 $\mathbf y=(1,0,0,0,1)^\top$ 可知

$_1=1>0,_5=1>0$ ，

由互补松弛定理，原问题的松弛变量

$y_1 x_{2+1}=0,y_5 x_{2+5}=0$ ，

即 $x_{3}=x_{7}=0$ ．

由对应的方程组 $\begin{cases}_1+2_2=2\\3_1+_2=3\end{cases}$ 得 $\displaystyle x_1=\frac{4}{5},_2=\frac{3}{5}$ ．

所以原问题最优解 $\displaystyle \mathbf x^∗= \left(\frac{4}{5}, \frac{3}{5}\right)^\top, ⁡_{\max}=5$ .

看看，冯·诺依曼如何为“小人物”救场？——从袁亚湘院士的建议说开去

引自：颜基义柚子优化 3月14日

我国正在开两会，这是我国在历史重要的节点上，极其重要的事件。

作为参会的政协委员，袁亚湘院士最近在接受中国科学报采访中明确表示，“刚刚入职的青年科技人员没有受到应有的重视。”采取了错误措施，会“导向青年科技工作者‘急功近利’、追求数量，不利于引导广大科技工作者潜心研究、默默奉献，不利于青年科技人员的健康成长，不利于他们系好科研生涯中的第一颗‘纽扣’。”

为此，袁亚湘院士呼吁“为青年科技人员扎根学术、潜心研究重大问题和原创性科学问题营造良好环境。”

前些时候，习近平总书记在科学家座谈会上强调指出“科学成就离不开精神支撑”。这种精神，无疑包含了“甘为人梯，奖掖后学”，为优秀青年人的创新开拓条件、铺垫道路。这是关系到我国在今后几十年高质量发展的关键性大问题。

因此，袁亚湘院士的建议发表后，引起了较大反响。我本人不仅很赞同他的建议，同时让我联想到自己亲身经历的一些事情。

上个世纪八十年代初期，我以访问学者身份在康奈尔大学运筹学与工业工程学院研学时，学院主任尼姆豪思（George Nemhauser）教授兼任着《Operations Research Letters（运筹学通讯）（以下简称ORL）》这个杂志的主编，当时这份杂志的流量并不大。

一天，尼姆豪思教授向我推荐了一篇文章，是G.B.Dantzig（坦齐格）在《ORL》上发表的《REMINISCENSES ABOUT THE ORGINS OF LINEAR PROGRAMMING (关于线性规划源起的回忆)》。

于是，我到资料室查找到这篇文章，浏览后，很受触动，便立即复制下来（当时访问学者可以免费复制学术文章）。这篇文章一直保持至今，近日费了一番牛劲才从资料堆中翻找出来。

回想起来，尼姆豪思教授之所以让我阅读这篇文章，其用意兴许是让我了解学科成长的历史文化。正如一位哲人所说，历史“会给一个人带来生命的共鸣”。

我到康奈尔后，经过一段时间观察，发现这里的运筹学与国内的差距相当明显，这里有太多崭新的东西值得自己去学习，去了解。因此，我对尼姆豪思教授说，我想尽量多听听，多学学。他表示赞同，并说，无论是讨论班，还是课程，你都可以根据自己的需求有选择地参加。

事后看来，尼姆豪思向我推荐这篇文章，给我的印象相当深刻，它的作用和重要性，一点不亚于那些崭新的组合优化的知识。

坦齐格这篇文章，最动人的地方，是冯·诺依曼对他的支持，是学界“大人物”支持刚刚出道“小人物”极为精彩的故事。略加改写，就是一个动人的历史短剧。

与大多数运筹学的各个学科一样，坦齐格开创了线性规划，其产生源头也与二战有着密切的关系。

坦齐格(G.B.Dantzig) 1914.12.08—2005.05.13

1946年，坦齐格在美国空军担任审计员的数学顾问。工作很出色，同事们不希望他另谋他职，便采用“激将法”，向他提出挑战，看谁能够更早地把规划过程实现机械化，计算的效果更好。当时，他们接受的任务，多属于诸如分阶段的部署、训练和后勤供应等方面的计划安排问题。

在那个年代，所谓机械化，无非就是使用模拟设备或穿孔卡片设备那样的计算工具，因为，计算机尚没问世。为此，坦奇格就从模型着手，开启了他的研究。

在这个过程中，坦齐格曾受到前苏联的瓦西里·列昂季耶夫的影响，后者提出了经济上的投入产出模型。

坦齐格发现，列氏的“一对一”式的替代方式并不能满足他面临那些问题的“一对多”的需求。因为这个“多”所造成的计算量实在巨大，不可能用“蛮力”计算的方法给出最好的结果。

到了1946年末，坦齐格的模型趋于成熟，用一些典型的，数目仅仅是有限的迭代方式，便可以给出问题的最好结果，而不必使用“蛮力”去比较那些多如天文数字的所有方案。

值得指出的是，坦齐格的这种方案，非常适合用计算机来实现。尽管，坦齐格的模型是出现在计算机之前，但在计算机出现之后，其应用场景的拓展更是如虎添翼。

坦齐格模型与计算机，这两者意想不到的契合，令坦齐格非常感慨，他说，“计算机的作用如此巨大，它的每一次新的渗透，就会诞生一门新的学科”。

坦齐格开创的这门新学科，后来称之为“线性规划（Linear Programming）”，其相应的数学系统是，在满足线性方程或线性不等式这样数学系统的前提下，将一个特定的目标数值实现最小化。

坦齐格在1947年6月拜访了芝加哥大学考尔斯基金会的库普曼（Koopmans），后者对此相当兴奋。因为第二次世界大战期间，他也曾为盟军工作，考虑的问题则属于解决轮船的运输模型。这样的共同基础，使得库普曼很欣赏坦齐格的工作，两人一拍即合。

到1947年，坦齐格成功了，诞生了解决这类模型的单纯形方法（Simplex Method）！简单地说，这是一个由线性不等式构成的数学系统，在几何上犹似“球状”的多面体。坦齐格构建的方法，就是确保运算程序只在那个多面体的顶点上运行。一次迭代过程，就是从一个顶点运行到另一个顶点，并确保目标数值同时也得到改善。

由于这个多面体的顶点是有限的，于是就不必再去考虑那些“无穷”个现实的搭配情况。这意味着，坦齐格模型开创了又一个，用有限来取代无限的数学系统及其方法。

这是很了不起的，具有很高的睿智“含金量”。即便在当今信息时代，依然有人以线性规划为背景算法，构建AI决策平台。

然而，坦齐格当时还没认识到这种方法到底有多么强大。于是，决定去咨询“伟大的”约翰尼·冯·诺依曼。

Von Neumann .png

冯·诺依曼(Von Neumann ) 1903.12.28—1957.02.08

时间是1947年10月3日，地点是普林斯顿高等研究院。

开始时，坦齐格还像与普通人交谈那样，前面做了很多铺垫性的陈述。对此，冯·诺依曼不耐烦地说“直说要点吧（Get to the points）”。于是在不到一分钟的时间里，坦齐格立即把问题的几何和代数形式一股脑地全都铺摆在黑板上。

冯·诺依曼站起来说:“哦，原来如此！”然后，他就大讲起来，足足讲了一个半小时。冯·诺依曼这样的举动，这样丰富的内容，让坦齐格惊讶不已。后者回忆说，当时“自己的眼睛睁得大大的，嘴巴张得大大的，…”。因为，在这之前，坦齐格虽说搜索了大量文献，可是并没有发现冯·诺依曼写过这方面的文章。坦齐格心想，冯·诺依曼冯实在太了不起了。

针对坦齐格的惊愕，冯·诺依曼接下来，对他面前这位年轻人这样解释说：坦齐格你不要认为我像个魔术师，灵光一动就把这些东西一下子就从袖子里变出来了。

其实，冯·诺依曼解释说，他最近刚和奥斯卡·摩根斯坦（Oscar Morgenstein）合作完成了一本书，关于博弈论的。冯·诺依曼在坦齐格面前所写下的那些内容，正是要推测这两个问题（坦齐格线性规划与冯·诺依曼的博弈论）是等价的。在讨论中，冯·诺依曼还提到了这个理论的对偶问题，这是坦齐格原先在构建模型时并没考虑到的，后来的事实证明，这是极其重要的理论背景。

关于对偶理论，坦齐格在该文中谈到，他与普林斯顿数学系老主任艾尔·塔克（Al Tucker）以及他的学生库恩（H.Kuhn）和盖尔（D.Gale）之间也有交流。后者三人在博弈论、非线性规划和对偶理论方面均有历史性的创新工作。在运筹学圈子里，人们都熟知的那个Kuhn-Tucker条件，就是老塔克和他的学生库恩共同建立的。

（笔者注：顺便说一句，那位获得诺贝尔奖的纳什，也是老塔克的研究生，与库恩是同窗好友。后者为了老同学纳什顺利获奖，做了大量的工作，功劳大矣。在Sylvia Nasar的《a Beautiful Mind》一书中有这些描述。）

坦齐格在文中说，我记得后来在与塔克教授的一次谈话中，内容涉及对偶理论。这次谈话的内容非常有意思，现将他们之间的主要对话摘录如下。

塔克问道:“为什么你把二元性（笔者注：即对偶理论给相应的数学系统带来了二元论）归因于冯·诺依曼而不是我的团队？”
坦齐格答：“因为他是让我看到对偶理论的第一人。”
塔克说：“这很奇怪啊，因为我们没有发现任何关于冯·诺依曼的著作。我们有他的论文《最大化问题》。”
坦齐格说“没错，但我会给你寄一份我第一次与冯·诺依曼会面后写的论文。”该论文主题是关于“线性不等式定理”。论文给出了对偶性的第一个严格证明，时间是1948年1月5日。
塔克问:“你为什么不发表？”
坦齐格回答说:“因为这不是我的结果——这是冯·诺依曼的，我只不过是将这些内容写出来而已。这一直是我的行事方式。”

时至今日，学界无不公认冯·诺依曼是对偶定理的创始人，而塔克、库恩和盖尔则是第一个严格证明的发表者。

在坦齐格和塔克第一次见面后不久，在威斯康辛州举办计量经济学学会会议，参会者有著名的统计学家、数学家和经济学家，如霍特林（Hotelling）、库普曼、冯·诺依曼等，大都是今天众所周知的学界大人物。而坦齐格，则是一个年纪轻轻的无名之辈。这是坦齐格第一次面对如此杰出的听众，给他们介绍线性规划，他既感到紧张又很害怕。

坦齐格发言后，会议在主席主持下进入讨论阶段。可是会场寂静得很（笔者注：原文是斜体字，表明坦齐格当时对报告完毕之后的寂静多么令人不安）。好一阵子后，有一只手举了起来，是霍特林举手。对于霍特林这样的大人物（笔者注：huge也是斜体字）的提问，坦齐格的回应是来不得半点犹疑不决的。坦齐格在文章里说，霍特林过去很喜欢在大海里游泳，一旦他进入海里，据说连海平面都会上涨。就是这样一位巨大的男人在会议房间的后面站着，脸上富有表情，略带一点微笑，似乎世界的事情没有他不知道。

霍特林然后说:“但是我们都知道，这个世界却是非线性的。（笔者注：原文整句话都是斜体字，可见这句话对于报告人的影响分量多么沉重）”。坦齐格说，这句话的打击简直是“毁灭性”的。

那时的坦齐格，身处在那堆科技群雄之中，简直就是个几乎不为人知的小不拉子，正在挖空心思地考虑，该如何去回应霍特林这样一个棘手的难题。

突然观众中有人举起手来，那是冯·诺依曼，他说：“先生。主席先生，如果不介意，我想替报告人回答。“坦齐格当然同意，会议主席也同意。

冯·诺依曼是这样说：演讲者的标题是“线性规划”，他非常认真地陈述了这个系统的相关公理。如果您的问题能够满足这些公理，那就请使用这个程序。如果不满足，那就不必使用。

多么精彩的回答！

话音一落，冯·诺依曼就坐下来，会场自然地继续进行下去。就这样，冯·诺依曼给极其尴尬的坦齐格“救了场”。

话说回来，霍特林的问题当然是对的。因为世界就是高度非线性。只是初出茅庐的坦齐格，缺乏应对这样场景，并回应相关问题的经验。事实上也如此，坦齐格的线性不等式系统可以采用近似逼近的方式，处理所遇到的大多数非线性问题。

历史不存在“如果”，但是人们常常用“如果”来发问，让我们这样设想：如果当时冯·诺依曼不在现场；如果冯·诺依曼在现场，但没有给坦齐格救场，那将会发生什么后果呢？细加寻思和分析，恐怕也不会引起太大的问题，顶多给坦齐格留下一些心理阴影，并不会阻挡线性规划的发展和应用。

在进入上个世纪八十年代后，坦齐格自己成为学界“大人物”了，却依然在多个场合，或发表演讲，或发表文章，或撰写回忆录，多次叙述这个动人的故事。笔者过去讲课时，也讲过这个动人的故事。

冯·诺依曼的精神如此高尚，非常令人敬佩，值得仰视。坦齐格呢，又何尝不是如此！他多次引述这个故事，不仅是在享受恩惠后表达对冯·诺依曼的回馈，同时也有助于降低社会理念的熵值，让学界的清流浸润人心。

终归，学界不是商场，更不是战场，而是一条连绵不断，呼啸而去的浩荡长河，其中“前浪引后浪，后浪推前浪”的“非线性”互助与提携的关系，则是这条大河奔腾不息的重要活力。

关于坦齐格，可说是典型的“学二代”，其父Tobias Dantzig，是颇有影响的数学家，其著作《Number: TheLanguage of Science（数字，科学的语言）》的影响也不小。当小坦齐格没出名时，会说他是老坦齐格的儿子。后来要介绍老坦齐格, 则说，他是小坦齐格的父亲了。

关于冯·诺依曼对后学的奖掖，也不仅仅限于坦齐格。在笔者前不久撰写的关于哥德尔的文章里，也有同样的描述。在哥德尔刚刚博士毕业时，他的报告反响平平，这对于心态极为敏感的哥德尔来说，无疑盖上一层厚厚的阴影。只有冯·诺依曼慧眼识真金，给予极高的评价，给哥德尔很大的鼓舞。

最后说到华罗庚先生，他1931年破格调入清华大学后，连续获得好几次的破格提升，除却本人的异常勤奋，学术成果突出外，同样离不开“贵人”们的提携。在关于华罗庚最关键的“助教”资格讨论中，教授团队的意见分歧很大，相互争持不下。毕竟让一个仅仅具有初中证书的人，要从行政岗位转为教学岗位，并承担起大学的教学任务，这个跨度确实大得惊人。清华，终归是全国最好的大学啊。然而，在这种情况下，作为理学院院长的叶企孙先生，他拍案而起，毅然决然做出最后决定，说：“清华出了个华罗庚是件好事，不要被资格所限定。”

后来，华罗庚先生自己也成为了“甘为人梯，奖掖后学”的楷模，他这样回应时任总书记的胡耀邦：“团结起来，为建造我们的通天塔而献身，这是我们每个科学工作者的职责啊！”他的实际行动，比起这些话语，更具有感动人的巨大力量。

从冯·诺依曼到坦齐格，再到中国的熊庆来、杨武之和叶企孙，再到后来的华罗庚，奖掖后学，从来就是科学的良好传统，是滋养科学创新的活水，国内国外，盖莫能外。

千年传灯，日月成诗，此乃大矣！

一、线性规划一般形式的对偶