案例1:“你好我好”的抓钱博弈
•假如甲乙两个人参加一个“抓钱”游戏,游戏开始时,每个人面前的托盘上会长出钞票。
u开始时刻1:甲前面的托盘上有1元钱,乙面前的托盘上也有1元钱,甲处于决策的位置。他有两种选择,把钱拿走或不把钱拿走,
–如果甲选择把1元钱拿走,乙也可以把1元钱拿走,游戏结束;
–如果甲选择不把钱拿走,游戏进入时刻2。
u时刻2:这时,甲的托盘上变成有2元钱,乙的托盘上也变成有2元钱,轮到乙处于决策位置。他同样有两种选择,把钱拿走或不把钱拿走。
–如果乙选择把2元钱拿走,甲也可以把2元钱拿走,游戏结束;
–如果乙选择不把钱拿走,游戏进入时刻3。
u时刻3:甲前面的托盘上变成有3元钱,乙面前的托盘上也变成有3元钱,甲再次处于决策的位置。他仍然有两种选择,把钱拿走或不把钱拿走,
–如果甲选择把3元钱拿走,乙也可以把3元钱拿走,游戏结束;
–如果甲选择不把钱拿走,游戏进入时刻4。
u时刻4:甲的托盘上变成有4元钱,乙的托盘上也变成有4元钱,又轮到乙处于决策位置。他还是有两种选择,把钱拿走或不把钱拿走。
–如果乙选择把4元钱拿走,甲也可以把4元钱拿走,游戏结束;
–如果乙选择不把钱拿走,则每人奖励5元,游戏结束。
•甲乙两人的博弈不是同时决策,而是轮流决策,以“甲— 乙—甲—乙”的次序进行,这样的博弈叫序贯决策博弈,是动态博弈。
•序贯决策博弈因为决策有先有后,一般不采用矩阵型表示方法,而多采用“树型”表示方法,正式的说法是博弈的展开型表示。
•我们可以将“抓钱博弈”表达成下面的博弈树(如图3-1)
u黑圆点是决策点
u黑菱形是末端节点
u大黑圆点是博弈树的根,并且每一博弈树只有一个根
u从一个节点指向另一个节点的“枝”,叫做棱

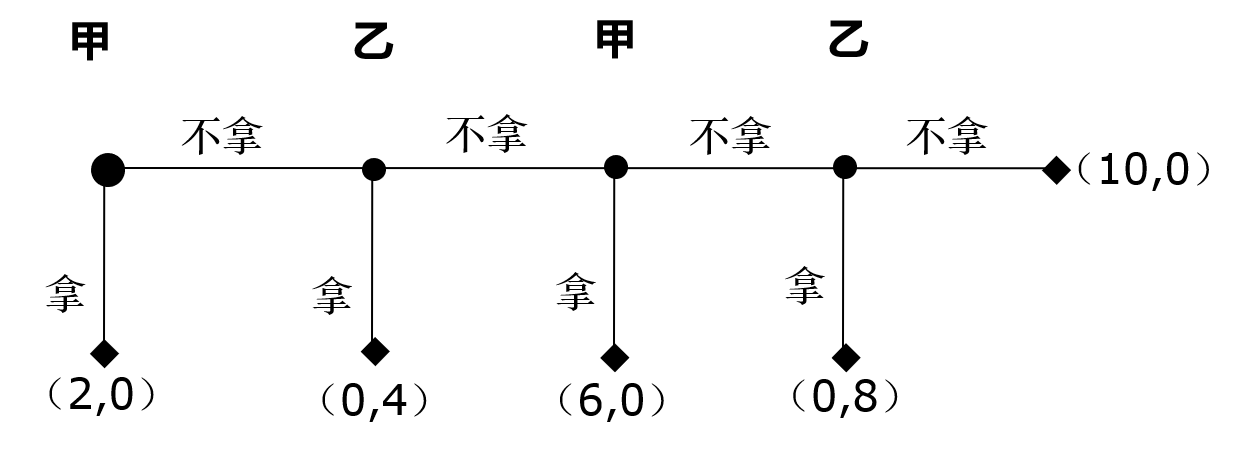
案例2:“你死我活”的抓钱博弈
u开始时刻1:甲的托盘上有2元,乙的托盘上没有钱,甲处于决策的位置
–如果甲把2元拿走,游戏结束,乙的收益为0;
–如果甲不把钱拿走,游戏进入时刻2。
u时刻2:甲的托盘没有钱,乙的托盘上变成有4元,乙作决策
–如果乙把4元拿走,游戏结束,甲的收益为0 ;
–如果乙不把钱拿走,游戏进入时刻3。
u时刻3:甲的托盘6元,乙的没有钱,甲作决策
–如果甲拿走6元,游戏结束,乙的收益0;
–如果甲不把钱拿走,游戏进入时刻4。
u时刻4:甲的托盘0元,乙的有8元,乙作决策
–如果乙拿走8元,游戏结束,甲的收益为0;
–如果乙不把钱拿走,则奖励甲10元,游戏结束,乙的收益为0。