广义胡克定律

在研究单向拉伸与压缩时，已经知道了在线弹性范围内，应力与应变成线性关系，满足胡克定律

此外，轴向变形还将引起横向尺寸的变化，横向线应变根据材料的泊松比可得出：

在纯剪切的情况下，根据实验结果，在切应力不超过剪切比例极限时，切应力和切应变之间的关系服从剪切胡克定律，即

 或 

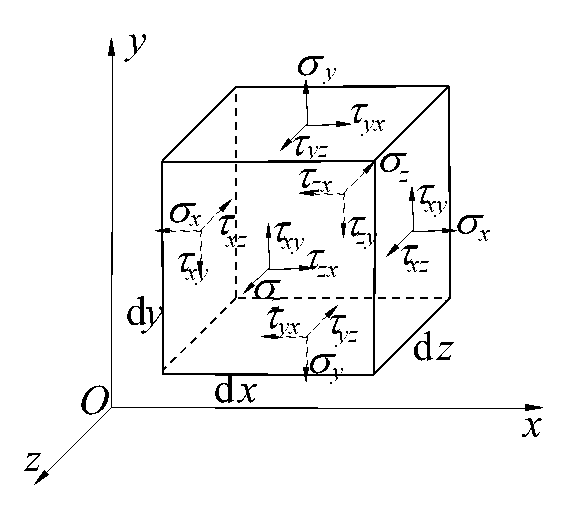
对于复杂受力情况，描述物体一点的应力状态，通常需要9个应力分量，根据切应力互等定律，只有6个是独立的。这种情况可以看成是三组单向应力和三组纯剪切的组合。

对于各向同性材料，在线弹性范围内，处于小变形时，线应变只与正应力有关，与切应力无关；而切应变只与切应力有关，与正应力无关，并且切应力只能引起与其相对应的切应变分量的改变，而不会影响其它方向上的切应变。因此，求线应变时，可不考虑切应力的影响，求切应变时不考虑正应力的影响。于是可以把正图（a）分解为图（b）、（c）、（d），分别求出与各个应力分量对应的应变分量，然后进行叠加即可。

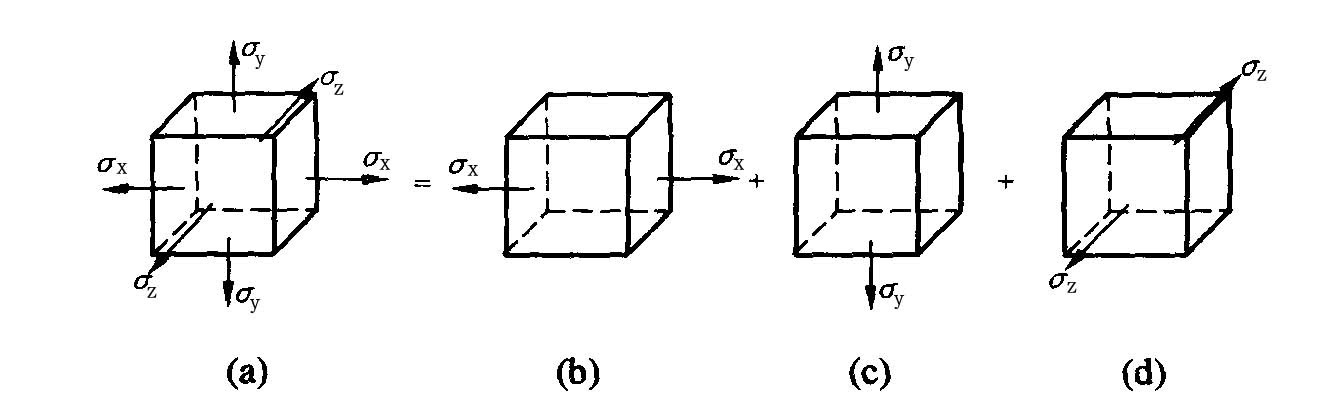
如在正应力σ_x单独作用时(图 (b))，单元体在x方向的线应变

在σ_y单独作用时(图 (c))，单元体在x方向的线应变为

在σ_z单独作用时(图(d))，单元体在x方向的线应变为

在σ_x、σ_y、σ_z共同作用下，单元体在x方向的线应变为：

同理，可求出单元体在y和z方向的线应变。最后得

对于切应变与切应力之间，由于切应变只与切应力有关，并且切应力只能引起与其相对应的切应变分量的改变，而不会影响其它方向上的切应变。因而在xy、yz、zx三个面内的切应变分别是

上述两组公式就是三向应力状态时的广义胡克定律。当单元体的六个面是主平面时，使x、y、z的方向分别与主应力的方向一致，这时有

广义胡克定律化为：

ε₁、ε₂、ε₃方向分别与主应力σ₁、σ₂、σ₃的方向一致，称为一点处的主应变。三个主应变按代数值的大小排列：ε₁ ≥ ε₂≥ε₃，其中，ε₁和ε₃分别是该点处沿各方向线应变的最大值和最小值。

对于平面应力状态（假设s_z=0,t_xz= 0,t_yz= 0） 

用主应力表示的平面应力状态的广义胡克定律为（设σ3=0）

若已知应变，求应力时可用下式

注意：

（1）应用公式要考虑应力的符号，按规定拉应力代入正值，压应力代入负值；

（2）ε的正负号代表伸长线应变或者缩短线应变。

体积应变

构件每单位体积的体积变化, 称为体积应变。

变形前单元体的体积：V=dxdydz

变形后：V₁=dx(1+e₁)· dy(1+e₂) · dz(1+e₃)

体积应变为

代入广义胡克定律简化后得：

改写为：

式中K称为体积弹性横量。

s_m称为平均应力。

结论：在线弹性范围内，体积应变与平均应力成正比，此即为体积胡克定律。

体积应变只与三个主应力之和有关，而与主应力之间的比例无关。因此，对不同的单元体，只要三个主应力之和相等，则体积应变相等。单元体的体积应变可用平均应力单元体来替代。