一、等直圆杆扭转实验观察

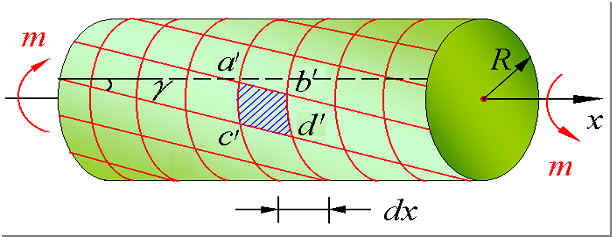
1.   圆周线变形后其形状、大小、间距保持不变。

2.   轴向无伸缩；

3.   纵向线变成斜直线，但仍为平行线。

平截面假设：横截面变形后仍为形状、大小、间距不变的平面；只是绕轴线发生了相对转动。

二、等直圆杆扭转时横截面上的应力

1.  变形几何关系

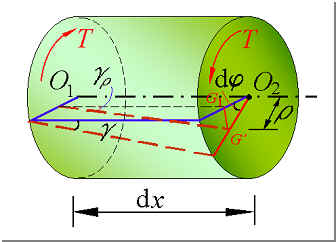
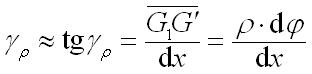
结论：距圆心为 r 任一点处的gr与到圆心的距离r成正比。

式中为扭转角沿长度方向变化率，在同一截面上不变。

2.  物理关系

根据剪切胡克定律：

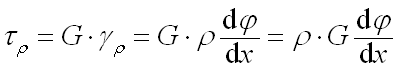
由此可见横截面上切应力成线性分布，如图所示。

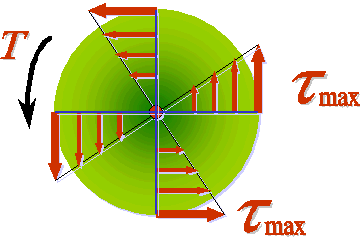
3.  静力学关系

在横截面上取一微小面积dA，合力为，考虑静力学关系。

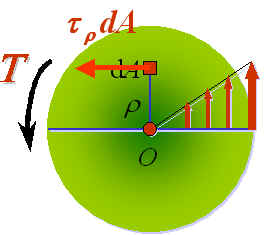
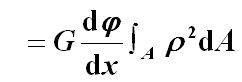
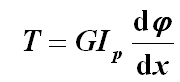
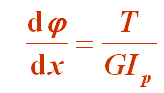
此式为扭转变形的基本公式。将上式代入由物理关系导出的切应力公式中得：

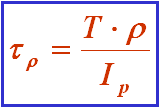
此即为横截面上距圆心为r处一点的切应力计算公式。

4.  公式讨论

（1）适用范围：线弹性材料、小变形、等圆截面直杆受扭。

（2） 式中：T—横截面上的扭矩，由截面法通过外力偶矩求得。r —该点到圆心的距离。Ip—极惯性矩，纯几何量，无物理意义。

（3）由实心圆截面杆推出，可适用于空心圆截面杆，只是Ip值不同。

对于实心圆截面：                     

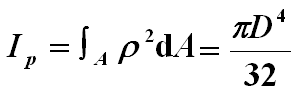
对于空心圆截面：

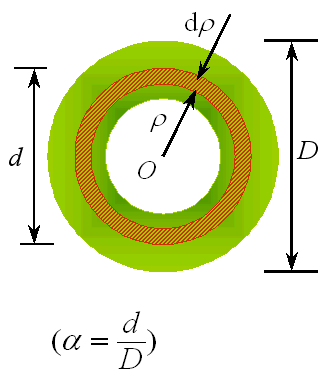
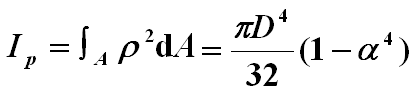
（4）应力分布

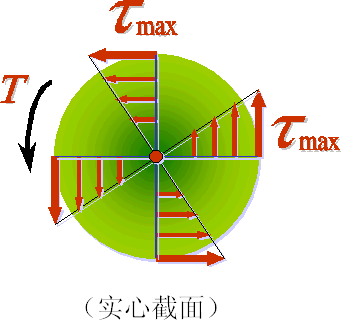
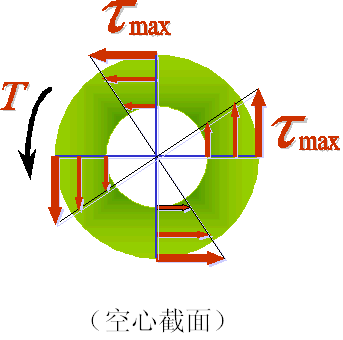
（5）最大切应力

根据切应力分布图可见，最大切应力发生在圆轴外表面各点，将代入切应力计算公式得：

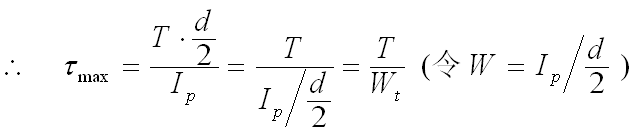
三、圆轴扭转时的强度计算