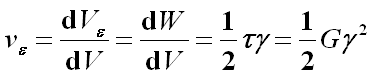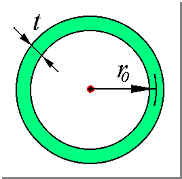
一、变形观察

变形前：在薄壁圆筒表面画等间距的纵向线与圆周线。

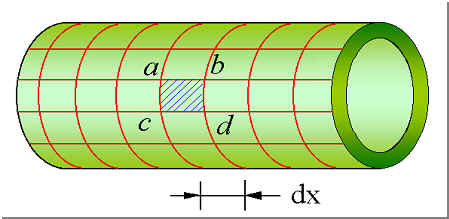
在圆筒左右施加大小相等，转向相反的一对外力偶。

变形后：

（1）圆筒表面的各圆周线的形状、大小和间距均未改变，只是绕轴线作了相对转动。

（2）各纵向线均倾斜了同一微小角度γ。

（3）所有矩形网格均歪斜成同样大小的平行四边形。

取如图所示的微小矩形单元体进行研究：

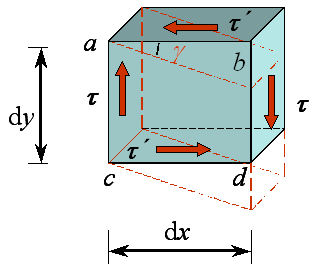
推论：

（1）纵、横截面上无正应力。

（2）横截面上各点处，只产生垂直于半径的均匀分布的剪应力t ，沿周向大小不变，方向与该截面的扭矩方向一致。

（3）切应力分布如图所示。

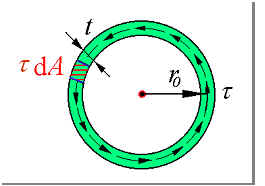
二、薄壁圆筒扭转时横截面上的切应力

考虑静力学关系，横截面上的分布力系合成为扭矩：

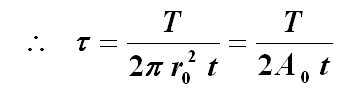
上式为薄壁圆筒受扭时横截面上切应力的计算公式，式中A0为平均半径所作圆的面积。  

三、切应力互等定理

考虑微小矩形单元体的平衡：

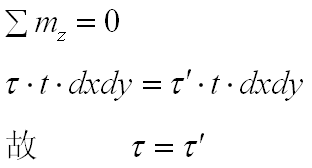
此即为切应力互等定理。定理表明：在单元体相互垂直的两个平面上，切应力必然成对出现，且数值相等，两者都垂直于两平面的交线，其方向则共同指向或共同背离该交线。

单元体的四个侧面上只有切应力而无正应力作用，这种应力状态称为纯剪切应力状态。

四、剪切胡克定律

考虑长度为L、关系为R的薄壁圆筒，两端受力偶作用，在弹性范围内，扭转角为φ，切应变为γ。

 在小变形的情况下，j与g的关系：

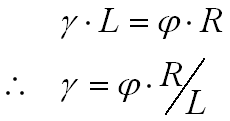
 m与t的关系：

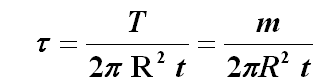
由实验测定的与的j－m曲线可得到切应力与切应变关系曲线如下图所示。

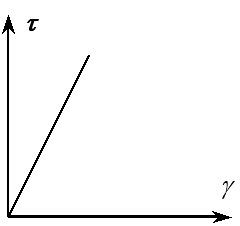
剪切胡克定律：当切应力不超过材料的剪切比例极限时（)，切应力与切应变成正比关系。

式中：G是材料的一个弹性常数，称为剪切弹性模量，因g 无量纲，故G的量纲与t 相同，不同材料的G值可通过实验确定，钢材的G值约为206GPa。

剪切弹性模量、弹性模量和泊松比是表明材料弹性性质的三个常数。对各向同性材料，这三个弹性常数之间存在下列关系：

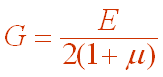
五、 剪切应变能密度

单元体微功：

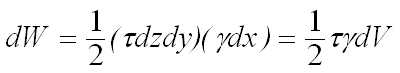
剪切应变能密度：