算法的基本概念
上一节
下一节
算法的五大特征:
输入:算法有零个或多个输入量
输出:算法至少产生一个输出量
确定性:算法的每一条指令都有确切的定义
可行性:算法的每一条指令都必须足够基本,可以通过已经实现的基本运算执行有限次实现
有穷性:算法必须总能在执行有限步之后终止
程序 = 算法?
不等于,程序是算法用某种程序设计语言的具体实现,程序不一定满足算法的五大特征,如操作系统是一个无限循环中执行的程序,不满足有穷性,但操作系统的各种任务当成一个单独的问题来看,每一个问题的子程序都通过特定的算法来实现。
算法设计的目标
算法设计的目的是求解问题,设计目标应满足如下几个:
正确性:要求算法能够正确地执行预先规定的功能和性能要求。
可使用性:要求算法能够方便的使用。
可读性:算法易于人的理解,逻辑清晰,简单的,结构化的。
健壮性:算法具有很好的容错性,即提供异常处理,能够对不合理的数据进行检查,不经常出现异常中断或死机现象。
高效率与低存储量需求:通常,算法的效率主要指算法的执行时间,对于同一个问题如果有多种算法可以求解,执行时间短的算法效率高。算法存储量指的是算法执行过程中所需的最大存储空间。效率和低存储都与问题的规模有关。
精确、启发、近似和随机算法?
精确算法:总能保证求得问题的解
启发式算法:通过使用某种规则、简化或智能猜测来减少问题求解时间
近似算法:致力于快速寻找近似解而不执着于最优解的算法
随机算法:执行过程中需要做出某些随机选择的算法
算法描述方法
自然语言描述、流程图、伪代码、程序设计语言等
算法性能与性能评价
指程序运行时所需的内存空间量和计算时间,包括系统开销和求解问题本身的开销。
评价方法:解析方法、实验测量方法(未必准确)
算法复杂度
算法复杂性是算法运行所需要的计算机资源的量,只依赖于算法所解问题的规模、算法的输入和算法本身的函数。
时间复杂度 :使用解析方法时程序 p 的时间复杂度表示为输入量的函数关系。
空间复杂度 :程序 p 运行时所需的内存空间大小和实例特征的函数关系。包括指令空间(与实例特征无关的常数)、数据空间(常量、简单变量、复合变量、环境栈空间等)、复合变量所需空间(与问题实例特征有关)。
最好复杂度:在最理想的情况下,算法的复杂度,常用于给出一个算法的计算时间的下界,用来否定一个算法
最坏复杂度:在最糟糕的情况下,算法的复杂度,当应用对计算时间/空间有严格要求时,应做最坏情形分析,考虑最坏时间/空间复杂度。
平均复杂度:加权平均情况下,算法的复杂度。
问题的难易因素
决策与优化问题:二者的复杂性近似等价
输入长度:输入实例的二进制编码长度(如 0/1背包问题和合数问题的伪多项式时间复杂度)
非确定性算法::产生与验证,获取证书的非确定性。注意与算法的确定性(指令执行的无歧义性)区别。
| 分类 | 定义 | 典例 |
|---|---|---|
| 易解问题 | 存在一个多项式界的求解算法 | 数组求和 |
| 难解问题 | 不存在多项式界求解算法,即求解该问题算法的复杂性至少是指数级的 | 旅行商问题 |
| 不可解问题 | 不能被确定型图灵机求解的计算问题,即不存在任何算法能够求解的计算问题 | 停机问题,对角论证法 |
NP-完全问题
NP-完全问题是算法中的一个重要概念
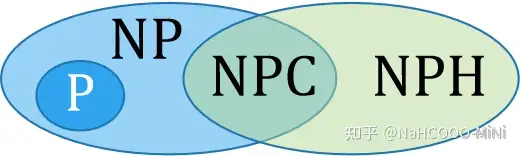
| 分类 | 定义 |
|---|---|
| P | 能够被确定性图灵机在多项式时间内求解的问题 |
| NP | 有不确定的多项式界算法的判定问题,包含P类问题 |
| NPH (NP-hard) | 所有NP类问题都可以多项式规约到NP-hard问题 |
| NPC | 既是NP问题又是NP-hard问题 |
注:多项式规约,记作X≤pY ,当且仅当存在一个多项式界的确定性算法 T,满足对 X 的每个输入实例 x 生成一个实例T(x) , x 是 X 的合法输入实例且对应 yes答案 ⇔ T(x)是 Y 的合法输入实例且对应 yes答案,意味着 X 至多和 Y 一样难。
算法分析
渐进分析
忽略掉 T(n)系数与低阶项, 仅关注高阶项(可用 Lim证明法)
渐进记号(重点)
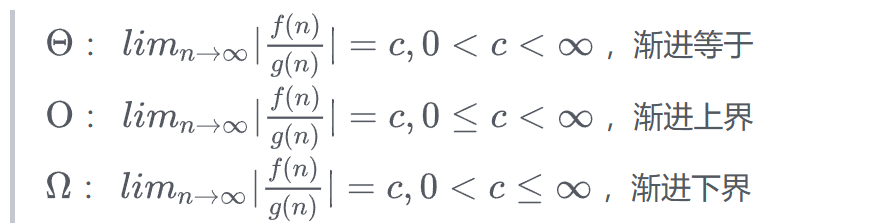
常用渐进比较(重点)

常用渐进等式
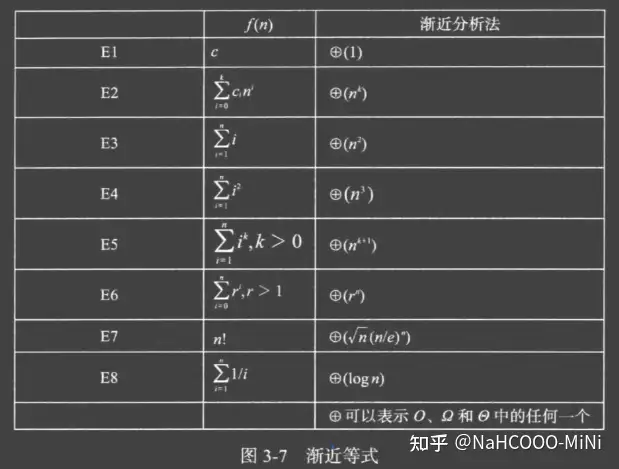
基本操作的执行时间必须是常数 s
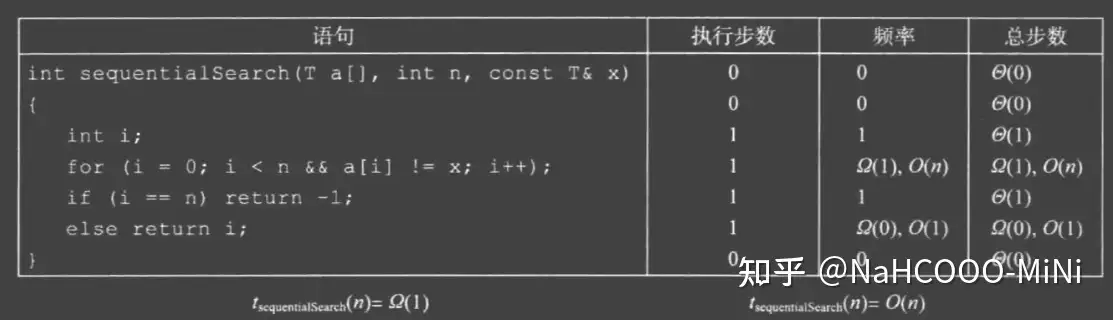
步(频率)计数法
程序步的执行时间必须是常数 s

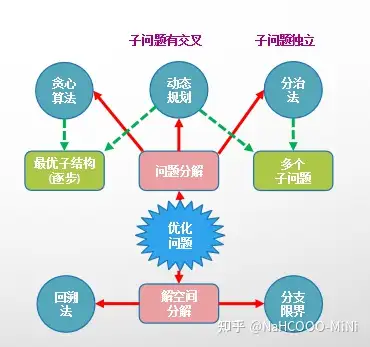
 五大算法
五大算法| 基本思想 | 特点 | 重点 | 难点 | |
|---|---|---|---|---|
| 贪心 | 核心是最优化问题,在其限制条件和优化函数的作用下,使优化函数取得最佳值的可行解为最优解(贪心选择过程与性质) | 不一定能找到最优解 | k-优化 | 贪心正确性证明 |
| 分治 | 分:将大问题分成相同类型的小问题 治:小问题可以在常数时间内解决 合:已知小问题的解可以合并共同解出大问题的解 | 巧用递归 | \ | \ |
| 动态规划 | 一个问题的解决方案是一系列子问题决策的决策的结果 每一步的决策都是循序渐进的,后进行的决策会受到先前决策的影响 | 最优子序列 | 状态转移方程 回溯确认方案 | \ |
| 回溯 | 组织解空间内系统性的搜索,类比深度优先搜索(DFS),搜索并回溯尽所有活结点,则是搜索结束的标志。 | 一个点有机会被多次激活为E-结点 | E-结点:当前所处的结点位置 活结点:可被再次转换为E-结点的结点 死结点:不能在被激活的结点 状态空间树、限界条件 | 对比分支限界,分清搜索结点顺序 |
| 分支限界 | 根据活结点表的优先级对解空间进行 | 被激活过的E-结点不可能再次被激活 | 活节点表三种形式FIFO(队列)、LIFO(堆栈)、优先队列(堆) 状态空间树、限界条件 | 对比回溯,分清搜索结点顺序 |
对于经典算法的学习,主要基于五大类算法,对应到各种具体应用问题上,建议以以下模式学习
适用条件+算法分类+算法设计+算法分析+经典例题(理论)+代码实现+一般化扩展(引申出更多问题)