如果想了解某一特定人群的平均身高、平均消费水平情况，或者想比较两个学校的教学水平差异，该如何做呢？解决此类问题需要对相应的总体的参数进行某种判断，此处判断的统计术语叫作估计或检验。

所谓估计指的是对总体的某个参数，如平均身高、平均消费水平做出的一个推断或结论，需要强调的是，估计是不唯一的，比如群体的身高可以用所有人的平均身高作为估计结果，也可以用最高身高和最低身高者两人的身高平均值作为估计结果，甚至可以用群体中第一个见到的人的身高作为估计结果。既然估计是不唯一的，那么，对于总体的同一个参数的不同估计来讲自然会有优劣之分，评判多个估计的好坏就需要给出“好”的估计的评价标准。

在统计推断中，我们需要依次回答以下问题：1）总体一定是服从某种分布吗？2）如果总体服从某一分布，是什么分布？3）如果已经确定服从某一特定分布（假设正态分布或均匀分布），那么分布中的参数信息如何确定？若干个总体之间参数是否有区别？

回答第一个问题。我们认为现实生活中很多事件都是充满随机性的，而随机事件的发生蕴藏一定的规律，这些规律所蕴含的信息都在总体分布中有所体现，分布是我们对现实生活中随机事件发生规律的抽象化总结，是一种理想化的工具。首先明确一点，现实中随机事件的发生是否和理想化的分布相对应并不知道，但是从经验来看，很多事件确实近似服从理想化的分布，从现实生活中的事件总结的规律也符合理想化分布的规律，因此，我们相信总体“应该”服从某种分布。这是统计推断的基础和前提。

回答第二个问题。我们现在相信总体服从某一分布，那么总体服从什么具体分布呢，是正态分布、指数分布还是均匀分布，或者其他分布？在这里，我们默认的假定是总体服从某一特定分布（只假定已知分布的形态特征，但是分布的参数不做假定），比如直接假定某地区人群身高服从正态分布，消费水平服从指数分布等等，这里的正态分布和指数分布可以调整成任何合适的分布，在作统计推断之前默认会做分布除参数外其他信息都已知的假定。

回答第三个问题。如果分布已经知道了，下面的问题就是对分布中未知的参数进行估计或对若干个总体参数进行检验的问题了。因此，估计方法和假设检验方法是本章学习的重点。为了讲授估计和检验检验方法，学习一些基础的统计推断知识是必要的。6.1给出了统计推断中需要用到的抽样分布知识，6.2节讲授了统计推断中常用的大数定理和中心极限定理。对于6.1节的内容需要简单了解一下，6.2节的理论知识重在理解其思想本质。

抽样分布的基本概念

由于总体是唯一的、固定不变的，故参数往往是一个未知的常数；而样本不唯一，且一旦抽取出来，就称为已知，故统计量是随机变量，它的取值是随着样本的变化而变化的。抽样的目的就是要根据样本统计量去推断总体参数。比如常用样本均值去推断总体期望，用样本方差去推断总体方差，以上这些做法的理论依据就是——样本统计量的抽样分布。

统计量是随机变量。抽样分布就是统计量的概率分布。如样本均值的概率分布、样本比例的概率分布、样本方差的概率分布等都称为抽样分布。它是由样本统计量的所有可能取值形成的相对频数分布。由于现实中不可能将所有可能的样本都抽出来，因此抽样分布实际上是一种理论分布。它可能是某一确定的分布，也有可能是一种极限分布。抽样分布理论在推断统计中具有重要的作用，它是后续参数估计和假设检验的理论依据和基础。

三大重要分布

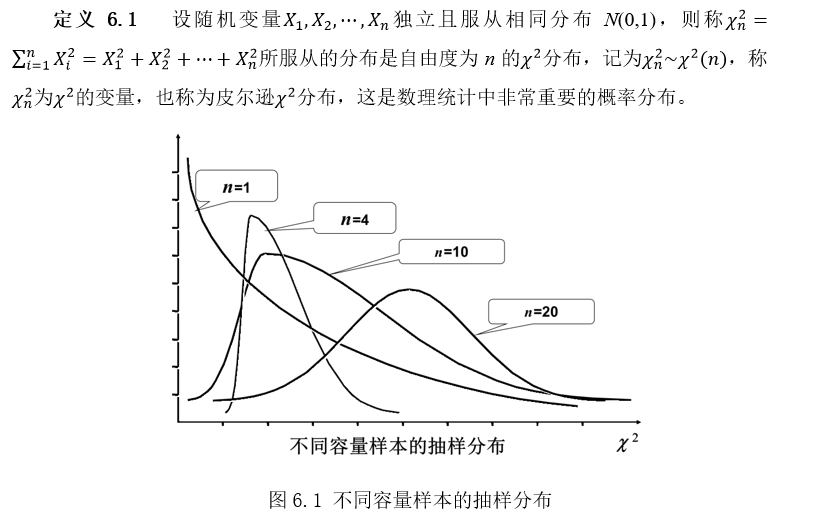
1.卡方分布

2.t分布

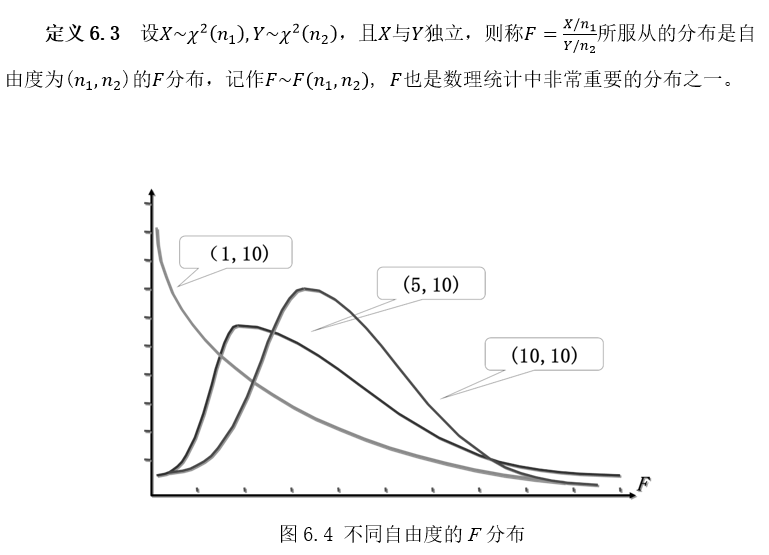
3.F分布