Mathematica软件简介

Mathematica是一个功能强大的计算机数学软件，可以同时完成数值计算、符号演算、图像制作和编程等各项功能．

1、启动进入Mathematica系统．

2、Mathematica工具按钮

在工作屏幕上方设有一组常用工具按钮，它们的主要功能如下：

新建、打开、存盘、打印按钮

剪切、拷贝、粘贴、清除按钮

计算、动画、图形Postscript、声音播放按钮

3维图形视点选择、颜色选择、中断、帮助按钮

3、输入和计算表达式

Mathematica的工作屏幕Notebook．对Notebook进行新建、打开、保存、编辑修改和打印等文件操作．Notebook 文件在存盘时被自动保存成后缀是 .ma的文件．

向Notebook键入作图表达式：Plot[Sin[x]，{x，-Pi，Pi}]；

然后对表达式进行计算．

计算表达式的命令方式有：

1）点击运行按钮；2）按Shift+回车键；3）按小键盘的回车键（在非数字状态下）．

系统完成计算机后会输出结果，并自动在输入行加入显示标记In[1]：=，在输出行加入显示标记Out[1]：=．

4、保存文件

在完成一个Notebook之后，需要存盘保存．存盘有如下方法：

1）点击存盘按钮后，在对话框中给定文件的路径和名称，回车即可．

2）在文件操作菜单File中选择Save．

3）在文件操作菜单File中选择Save As，可以用另外的文件名来保存文件．

5、Mathematica软件的基本命令

1）双击Mathematica软件图标即可启动Mathematica软件．

提示符：.“In[1]：=”中，“In”表示“输入”，数字“1”表示输入命令的序号；在运行结果之前会自动出现提示符．

“Out[1]：=”，其中“Out”表示“输出”．

同时按下Shift与Enter键即可执行相应的命令．

2）若输入的数据是精确的，计算结果保留精确数字．

若要计算近似值，可用函数N[x]或x//N表示x的近似值．

N[x，n]给出x的n位有效数字．

如：In[1]：= N[3^（）]   Out[1]=1.44225   In[2]：=3^（）   Out[2]=

3）常用的常数与函数

常用的函数：Abs[x]（|x|）；Sin[x] （sinx）；Cos[x]（cosx）；Tan[x]（tanx）；Cot[x]（Cotx）；

Sec[x]（secx）；Log[x]（lnx）；Exp[x]（）；Log[a，x]（ ）；Sqrt[x]（）；

N[x，n]（x的n位有效数字）；Round[x]（x经四舍五入的整数）；Mod[n,m]（n关于m的模）；Ceiling[x]（不小于x的最小整数）；Max[x1，x2，...]（max（，…）；Min[x1，x2，…]（min（…））；

常用的常数：Pi（）；E（e）；Infinity（）；-Infinity（-）

在Mathematica软件中，英文字母大小写严格区分，函数与命令的第一个字母必须大写．函数与命令后面的表达式要放在括号里．

4)定义函数

例如：In[1]：=f[x_]：=Sin[x]

如要计算函数f[x]在某一点x=的值，可用下面的命令：f[]或f[x]/. x->

例如：In[2]：=f[Pi/2]　　　　　　　　　　　Out[2]=1

　　　In[3]：= cos[x]/ . x->Pi/2　　　　   Out[3]=0

　　　In[4]：=g[x_，y_]：=；

　　　        g[x，y]/.{x->1,y->2}             Out[4]=5

5) 关系运算

        

x==y	相等	X>y	大于	X〈y	小于
X！=y	不相等	X>=y	大于或等于	X〈=y	小于或等于

例如：In[1]：=3>=2　　　　　　　Out [1]=True

In[2]：=2〈3〈4〈3　　　　Out [2]=False          

In[3]：=3！=2！=3！=4　　 Out [3]=False

6)作图

(1)二维函数作图

给出一个一元函数及其作图区间，用Plot语句可以作出函数在相应区间上的图形．

例如： In[1]:=Plot[Sin[x],{x,0，2Pi}]；

Plot命令的一般形式为: Plot[f[t]],{x,xmin,,xmax},选项]

(2)二维参数作图

用ParametricPlot命令，其一般形式为：ParametricPlot[{x[t],y[t]},{t,tmin,tmax},选项]

例如：In[2]:=ParametricPlot[{Cos[t],Sin[t]},{t,0,2Pi}]；In[2]中输入的是一个圆的参数方程，可画出一个圆．

7)Mathematica中常见操作说明

(1) 括号的设别

（） 表示分组的圆括号；

｛a,b,…｝ 表示集合的花括号；f[x]       表示函数的方括号；

  V[[I]]     表示目录索引的双括号．

(2) 清除

Clear[x]或x=.       取消对x的赋值．

注意：使用变量前先清除变量以前的定义．

(3) %的作用

％可用于表示上次计算的结果；％％表示上上次的计算结果．

（4）关于分号“；”的使用

Mathematica语言规定“；”号为其语句分割符，当其后不再有mathematica语句时，其含义为要求系统不再输出该语句的运算结果中Out后面的结果；若其后还有其它语句，则认为两语句为并列关系，且最后一个语句的结果为它们顺序执行后的结果．

函数及图形绘制

实验目的  

通过实验，体会函数与图形的关系，了解基本初等函数的处理及计算，学会使用Plot作图函数，了解使用选择项对图形的组合、外观进行修饰的初步方法，学会使用Show函数进行图形的组合．

基本命令

1.基本初等函数在Mathematica中计算；

输入Sin[]；Sin[Pi/3]；Sin[60Degree]；Sin[60⁰] 观察结果并记录．

2.绘图命令绘制二维图形；

1)Plot[f[x],{x,a,b}]在区间[a,b]上绘制函数f(x)的二维图形；

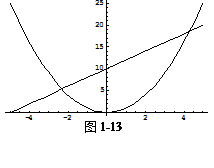
在同一坐标系内画出y=,y=2x+10,-5x5的图形；

输入：

（如图1-13）

注意使用分号；

2)Plot[{f[x],g[x]},{x,a,b}]在同一坐标系中绘制两个（或多个）函数的图形；

3)利用PlotStyle改变图形的外观．

PlotStyle->样式       绘图样式：颜色深浅GrayLevel[x],

虚线方式Dashing[{,,…,}],

图形绘制的宽度Thickness[r]．

颜色RGBColor[a,b,c],  a,b,c=0,1．

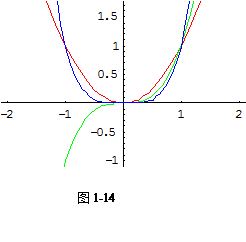
在同一坐标系内画出y=,y=,y=,－２x２的图形（如图1-14）；

输入：  

3.图形组合Show

Show[g1,g2,…]在同一坐标系中显示几幅图形．

将y=在[-３,３]上的图形和y=sinx在[,]上的图形，在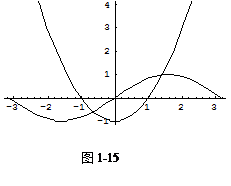同一坐标中显示（如图1-15）．

输入：

               

函数的极限

实验目的  加深对数列极限概念的认识；掌握命令Limit的使用，学会极限，以及左右极限的计算，并会解决与极限有关的一些实际问题．

基本命令

1.  对极限定义的认识

用Table语句观察数列的前100项变化情况．

输入：A=N[Table[，{n，1，100}] ]

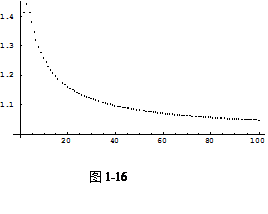
用语句ListPlot[a]画出散点图，借助于图形观察变化趋势．

将数列换成{}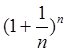，{}，观察结果（如图1-16）．

输入：         

2.  极限的计算

 Limit[表达式，趋向过程]  

如：求极限用命令Limit[f[x],x->x0]．

3.  利用Direction选项确定左右极限的计算；

左极限：Limit[f[x],x->x0,Direction->1]；（沿x 轴正向趋向于x0,即左极限）

右极限：Limit[f[x],x->x0,Direction->-1]；（沿x 轴负向趋向于x0,即右极限）

求下列函数的极限:(1)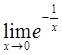;(2)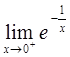

输入：

4. 计算在∞处的极限．（无穷大用∞表示或用Infinity表示）

输入：

；

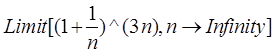
输入Limit[Sin[1/x],x->0],结果为什么是一个区间？

画出y=sin(1/x)在[-1，1]上的图形．

输入：

输出：