实验目的

观察无穷级数部分和的变化趋势,进一步理解级数的审敛法以及幂级数部分和对函数的逼近. 掌握用Mathematica求无穷级数的和, 求幂级数的收敛域, 展开函数为幂级数以及展开周期函数为傅里叶级数的方法.

基本命令

1. 求无穷和的命令Sum

    该命令可用来求无穷和. 例如,输入   Sum[1/n^2,{n,l,Infinity}]

则输出无穷级数的和为 命令Sum与数学中的求和号相当.

2. 将函数展开为幂级数的命令Series

    该命令的基本格式为:      Series[f[x],{x,x0,n}]

它将展开成关于的幂级数. 幂级数的最高次幂为余项用表示. 例如,输入    Series[y[x],{x,0,5}]

则输出带皮亚诺余项的麦克劳林级数

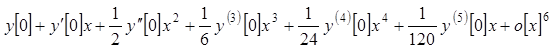
3. 去掉余项的命令Normal

在将展开成幂级数后, 有时为了近似计算或作图, 需要把余项去掉. 只要使用Normal命令.

例如,输入     Series[Exp[x],{x,0,6}]

              Normal[%]

则输出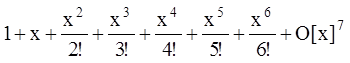      

             

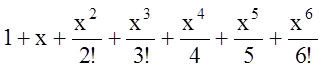
4. 强制求值的命令Evaluate

如果函数是用Normal命令定义的, 则当对它进行作图或数值计算时, 可能会出现问题.

 例如,输入fx=Normal[Series[Exp[x],{x,0,3}]]

Plot[fx,{x,-3,3}]

则只能输出去掉余项后的展开式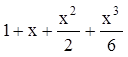 

而得不到函数的图形. 这时要使用强制求值命令Evaluate, 改成输入

    Plot[Evaluate[fx],{x,-3,3}]

则输出上述函数的图形.

实验举例

【例1】设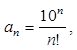 求.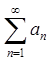

输入Clear[a];a[n_]=10^n/(n!);

vals=Table[a[n],{n,1,25}];

ListPlot[vals,PlotStyle->PointSize[0.012]]                               

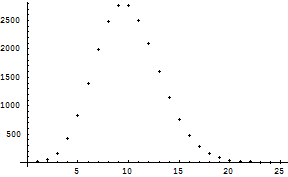则输出的散点图（如图10－5）,

从图中可观察的变化趋势. 输入       Sum[a[n],{n,l,Infinity}]

则输出所求级数的和.                          

求幂级数的收敛域

【例2】求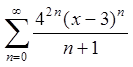的收敛域与和函数.                  

输入Clear[a];

a[n_]=4^(2n)*(x-3)^n/(n+1);

stepone=a[n+1]/a[n]//Simplify

则输出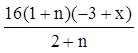    

再输入     steptwo=Limit[stepone,n->Infinity]

则输出    

这里对a[n+1]和a[n]都没有加绝对值. 因此上式的绝对值小于1时, 幂级数收敛; 大于1

时发散. 为了求出收敛区间的端点, 输入

ydd=Solve[steptwo==1,x]

zdd=Solve[steptwo==-1,x]

则输出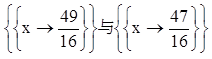 

由此可知,当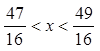时,级数收敛,当或时,级数发散.

为了判断端点的敛散性,

输入 Simplify[a[n]/.x->(49/16)]

则输出右端点处幂级数的一般项为

因此,在端点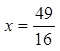处,级数发散.

再输入 Simplify[a[n]/.x->(47/16)]

则输出左端点处幂级数的一般项为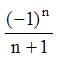

因此,在端点处, 级数收敛.

函数的幂级数展开

【例3】求的5阶泰勒展开式.

输入    serl=Series[ArcTan[x],{x,0,5}];Poly=Normal[serl]                                

则输出的近似多项式 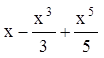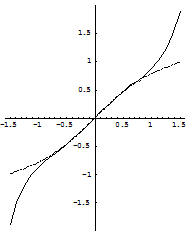通过作图把和它的近似多项式进行比较. 

输入    Plot[Evaluate[{ArcTan[x],Poly}],{x,-3/2,3/2},       

PlotStyle->{Dashing[{0.01}],GrayLevel[0]},AspectRatio->l]

则输出所作图形（如图10－6）,

图中虚线为函数,实线为它的近似多项式.