实验目的 

掌握用Mathematica绘制空间曲面和曲线的方法. 熟悉常用空间曲线和空间曲面的图形特征,通过作图和观察, 提高空间想像能力. 深入理解二次曲面方程及其图形.

基本命令

1.空间直角坐标系中作三维图形的命令Plot3D

命令Plot3D主要用于绘制二元函数的图形. 该命令的基本格式为

Plot3D[f[x,y],{x,x1,x2},{y,y1,y2},选项]

其中f[x,y]是的二元函数, x1,x2表示x的作图范围, y1,y2表示y的作图范围.

例如, 输入

Plot3D[x*y,{x,-2,2},{y,-2,2},BoxRatios->{1,1,2},PlotPoints->30]

输出函数的图形(如图7-36)

2.利用参数方程作空间曲面或曲线的命令ParametricPlot3D

用于作曲面时, 该命令的基本格式为

ParametricPlot3D[{x[u,v],y[u,v],z[u,v]},

{u,u1,u2},{v,v1,v2},选项]

其中x[u,v],y[u,v],z[u,v]是曲面的参数方程表示式.

u1,u2是作图时参数u的范围, v1,v2是参数v的范围.

用ParametricPlot3命令作出的图形,

输入

ParametricPlot3D[{r*Cos[t],r*Sin[t],r^2*Cos[t]*Sin[t]},{r,0,2},{t,0,2 Pi},PlotPoints->30]

     

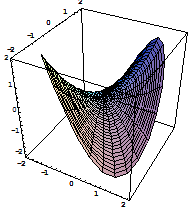
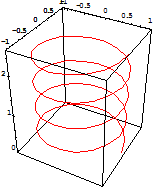
                             图7-36                                    图7-37

用于作空间曲线时,ParametricPlot3D的基本格式为

ParametricPlot3D[{x[t],y[t],z[t]},{t,t1,t2},选项]

其中x[t],y[t],z[t]是曲线的参数方程表示式.   t1,t2是作图时参数t的范围.

例如, 空间螺旋线的参数方程为

输入ParametricPlot3D[{Cos[t],Sin[t],t/10,RGBColor[1,0,0]},{t,0,8Pi}]

则输出了一条红色的螺旋线(如图7-37).

例1 作出球面和柱面相交的图形.

输入

g1=ParametricPlot3D[{2Sin[u]*Cos[v],2Sin[u]*Sin[v],2Cos[u]},{u,0,Pi/2},{v,0,2 Pi},DisplayFunction->Identity];

g2=ParametricPlot3D[{2Cos[u]^2,Sin[2u],v},{u,-Pi/2,Pi/2},{v,0,3},DisplayFunction->Identity];

Show[g1,g2,DisplayFunction->$DisplayFunction]

则输出所求图形（如图7-38）.

例2作出默比乌斯带(单侧曲面)的图形.

输入

Clear[r,x,y,z];     r[t_,v_]:=2+0.5*v*Cos[t/2];

x[t_,v_]:=r[t,v]*Cos[t]     y[t_,v_]:=r[t,v]*Sin[t]      z[t_,v_]:=0.5*v*Sin[t/2];

ParametricPlot3D[{x[t,v],y[t,v],z[t,v]},{t,0,2Pi},{v,-1,1},PlotPoints->{40,4},Ticks->False]

则输出所求图形（如图7-39）. 观察所得到的曲面, 理解它是单侧曲面.

 

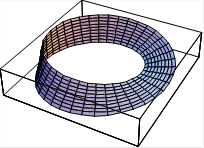
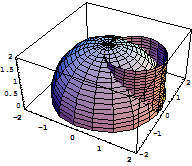
     图7-38                                              图7-39