实验目的 

掌握利用Mathematica计算多元函数偏导数和全微分的方法, 掌握计算二元函数极值和条件极值的方法. 理解和掌握曲面的切平面的作法. 通过作图和观察, 理解二元函数的性质和等高线的概念.

基本命令

1.求偏导数的命令D

命令D既可以用于求一元函数的导数, 也可以用于求多元函数的偏导数. 例如:

求对x的偏导数,则输入D[f[x,y,z],x]

求对y的偏导数,则输入D[f[x,y,z],y]

求对x的二阶偏导数, 则输入D[f[x,y,z],{x,2}]

求对的混合偏导数, 则输入D[f[x,y,z],x,y]

2.求全微分的命令Dt

基本格式为Dt[f[x,y]]

其输出的表达式中含有Dt[x],Dt[y],它们分别表示自变量的微分dx,dy.

3.在平面上作二元函数的等高线的命令ContourPlot

命令的基本格式为ContourPlot[f[x,y],{x,x1,x2},{y,y1,y2}]

例1设求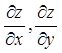和全微分dz.

输入Clear[z];z=(1+x*y)^y;D[z,x]；D[z,y]；Dt[z]

则有输出

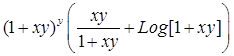
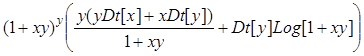
例2求曲面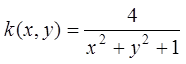在点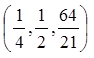处的切平面方程, 并把曲面和它的切平面作在同一图形里.

输入Clear[k,z];

k[x_,y_]=4/(x^2+y^2+1);(*定义函数k(x,y)*)

kx=D[k[x,y],x]/.{x->1/4,y->1/2};(*求函数k(x,y)对x的偏导数, 并代入在指定点的值*)

ky=D[k[x,y],y]/.{x->1/4,y->1/2};(*求函数k(x,y)对y的偏导数, 并代入在指定的值*)

z=kx*(x-1/4)+ky*(y-1/2)+k[1/4,1/2];(*定义在指定点的切平面函数*)

qm=Plot3D[k[x,y],{x,-2,2},{y,-2,2},PlotRange->{0,4},BoxRatios->{1,1,1},

PlotPoints->30,DisplayFunction->Identity];

qpm=Plot3D[z,{x,-2,2},{y,-2,2},DisplayFunction->Identity];

Show[qm,qpm,DisplayFunction->$DisplayFunction]

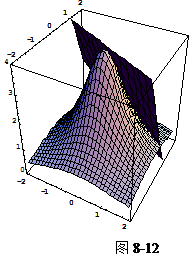
则输出所求曲面与切平面的图形（如图8-12所示）.

例3求的极值.

输入Clear[f];

f[x_,y_]=x^3-y^3+3x^2+3y^2-9x;

fx=D[f[x,y],x]

fy=D[f[x,y],y]

critpts=Solve[{fx==0,fy==0}]

则分别输出所求偏导数和驻点:

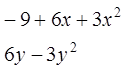
{{x->-3,y->0},{x->-3,y->2},{x->1,y->0},{x->1,y->2}}

再输入求二阶偏导数和定义判别式的命令

fxx=D[f[x,y],{x,2}];

fyy=D[f[x,y],{y,2}];

fxy=D[f[x,y],x,y];

disc=fxx*fyy-fxy^2

输出为判别式函数的形式:(6+6x)(6-6y)

再输入data={x,y,fxx,disc,f[x,y]}/.critpts;

TableForm[data,TableHeadings->{None,{"x ", "y ", "fxx ", "disc ", "f"}}]

最后我们得到了四个驻点处的判别式与的值并以表格形式列出.

X      y      fxx     disc     f

    -3      0     -12      -72     27

    -3      2     -12      72     31

     1      0      12      72     -5

    1      2      12      -72     -1

易见,当时判别式disc=72, 函数有极大值31;

当时判别式disc=72, 函数有极小值-5;

当和时, 判别式disc=-72,函数在这些点没有极值.

最后,把函数的等高线和四个极值点用图形表示出来,

输入d2={x,y}/.critpts;

g4=ListPlot[d2,PlotStyle->PointSize[0.02],DisplayFunction->Identity];

g5=ContourPlot[f[x,y],{x,-5,3},{y,-3,5},Contours->40,PlotPoints->60,ContourShading->False,Frame->False,Axes->Automatic,AxesOrigin->{0,0},DisplayFunction->Identity];

Show[g4,g5,DisplayFunction->$DisplayFunction]

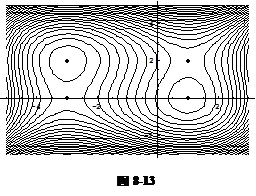则输出等高线图形（如图8-13所示）.

       从上图可见, 在两个极值点附近, 函数的等高线为封闭的. 在非极值点附近, 等高线不封闭. 这也是从图形上判断极值点的方法.