实验目的
本次实验学习常微分方程的解法，要求掌握Dsolve,NDSolve两个命令的用法，会求解常微分方程的应用问题．
实验内容
1、Mathematica命令Dsolve用于常微分方程的解析解；
①微分方程的通解；
命令：Dsolve[微分方程,y[x],x]
含义：给出独立变量为x的微分方程的通解y[x]．
注：微分方程中未知函数要表示成y[x]，而不能只用y，Mathematica认为y为常数，没有给定初值条件的微分方程的解包含一个任意常数，缺省情况下用C[1]表示，其它的常数（高阶方程）用C[2],C[3],…表示．
②使用定解条件求微分方程的特解；
命令：Dsolve[{微分方程，定解条件},y[x],x]
含义：求微分方程满足定解条件的特解．
③解微分方程组；
命令：Dsolve[微分方程组,{y[x], …,z[x]},x]
Dsolve[{微分方程组，定解条件},{y[x], …,z[x]},x]
2、NDSolve用于求常微分方程的数值解；
命令：NDsolve[{微分方程，定解条件},y,{x,xmin,xmax}]
含义：给出在方程中定义的微分方程以及初始条件所确定的解y的数值近似．其中独立变量x满足xmin≤x≤xmax．
3、利用Dsolve命令求解常微分方程的应用题．
实验步骤
1．Dsolve命令的使用；
1）微分方程的通解
①求解一阶微分方程
=x+y．
输入：
②求解微分方程
+y=0．
输入：
2）使用定解条件求微分方程的特解
①求
=y的通解和满足初始条件y(0)= 
(0)=2, 
(0)=
(0)=1的特解．
输入：
②求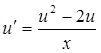
满足初始条件
的特解．
输入：
③求解
=x+y，初始条件y(0)=2的特解，然后给出解的图形．
输入 ：
3）解微分方程组
求解常微分方程组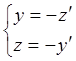
的通解和满足y(1)=1,z(1)=0的特解．
输入：
2、NDSolve用于数值近似；
①微分方程
初值条件y(0)=1,给出数值近似解．
注：Mathematica对近似值进行插值，即构造一个过这些点的光滑函数，并以InterpolatingFunction对象的形式返回解．
输入：
输出：
输入：
输出：
输入：
输出：
输入：
输出：
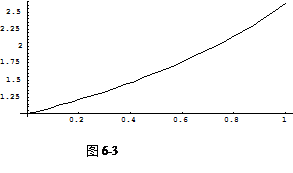
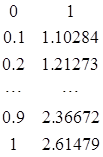
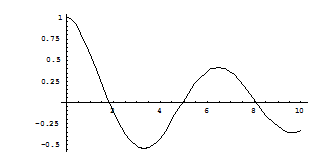
输入：
（如图6-3）
②画出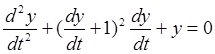
，y(0)=1,
(0)=0，在0≤t≤10上解的图形．
输入：
输出：
输入：
（如图6-4）
③对于
，分别画出它相对于初值条件为(0)=1，y(0)=-2,-1,0,1,2的五组解在0≤x≤30上的图形．
输入：
$
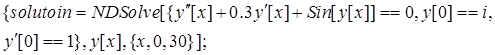
（如图6-5）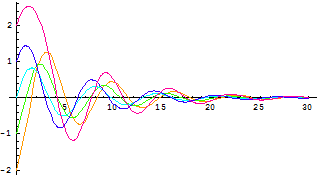
3、应用
有一种细菌，其繁殖速度正比于即时的细菌总数，如果从某时刻开始，一天后有500个细菌，两天后有1200个细菌，那么4天后有多少个细菌？
注：满足
，其中N为某时刻细菌的数目，k为比例常数，
t=1时N=500．
输入：
输出：
输入：
