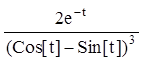实验目的  深入理解导数与微分的概念, 导数的几何意义. 掌握用Mathematica求导数与高阶导数的方法. 深入理解和掌握求隐函数的导数, 以及求由参数方程定义的函数的导数的方法.

基本命令

1.求导数的命令D与求微分的命令Dt

D[f,x]给出f关于x的导数, 而将表达式f中的其它变量看作常量. 

D[f,{x,n}]给出f关于x的n阶导数.

Dt[f]给出f的微分.

上述命令对表达式为抽象函数的情形也适用, 其结果也是一些抽象符号.

命令D的选项NonConstants->{…}指出{…}内的字母是x的函数.

命令Dt的选项Constants->{…}指出{…}内的字母是常数.

 

实验举例

【例1】求函数的一阶导数.

输入D[x^n,x]，则输出函数的一阶导数

注：在求导数时, 已经将指数n看作常数.

【例2】求函数的一阶导数. 并求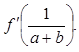

输入D[Sin[a*x]*Cos[b*x],x]/.x->1/(a+b)

则输出函数在该点的导数

 

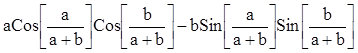
【例3】求函数的1阶到11阶导数.

输入Clear[f];f[x_]=x^10+2*(x-10)^9;D[f[x],{x,2}]

则输出函数的二阶导数

类似可求出3阶、4阶导数等等. 为了将1阶到11阶导数一次都求出来, 输入

Do[Print[D[f[x],{x,n}]],{n,1,11}]

则输出

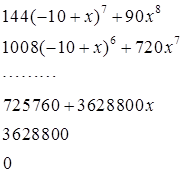
或输入Table[D[f[x],{x,n}],{n,11}]

则输出集合形式的1至11阶导数(输出结果略).

【例4】求函数与的微分.

输入Dt[Sin[2*x]]，则输出函数的微分2 Cos[2x] Dt[x]

再输入Dt[Sin[a*x]*Cos[b*x],Constants->{a,b}]//Simplify

其中选项Constants->{a,b}指出a,b是常数.

则输出函数的微分

Dt[x,Constants->{a,b}](aCos[a x]Cos[b x]-b Sin[a x] Sin[b x])

输出中的Dt[x,Constants->{a,b}]就是自变量的微分dx.

如果输入Dt[Sin[a*x]*Cos[b*x]]，则将a, b看作变量, 得到的是三元函数的全微分:

Cos[ax] Cos[b x] (x Dt[a]+a Dt[x])+(-x Dt[b]-b Dt[x] Sin[a x] Sin[b x]

【例5】求由方程确定的隐函数的导数.

方法1  输入deq1=D[2x^2-2 x*y[x]+y[x]^2+x+2 y[x]+1==0,x]

这里输入y[x]以表示y是x的函数. 输出为对原方程两边求导数后的方程deq1:

1+4x-2 y[x]+2y' [x]-2 xy' [x]+2 y[x]y' [x] == 0

再解方程, 输入Solve[deq1,y ' [x]]

则输出所求结果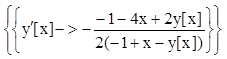

方法2  使用微分命令.

输入deq2=Dt[2 x^2-2x*y+y^2+x+2y+1==0,x]

得到导数满足的方程deq2:1+4x-2y+2 Dt[y,x]-2x Dt[y,x]+2y Dt[y,x]= =0

再解方程, 输入Solve[deq2,Dt[y,x]]，

则输出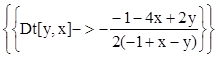

注意前者用y’[x], 而后者用Dt[y,x]表示导数.

2.求隐函数的导数及由参数方程定义的函数的导数

【例6】求由参数方程确定的函数的导数.

输入D[E^t*Sin[t],t]/D[E^t*Cos[t],t]，

则得到导数

再输入D[%,t]/D[E^t*Cos[t],t]//Simplify，

则得到二阶导数