实验目的

理解并掌握用函数的导数确定函数的单调区间、曲线的凹凸区间和函数的极值的方法. 理解曲线的曲率圆和曲率的概念.

实验举例

例3.1求函数的单调区间.

输入  f1[x­_]:=x^3-2x+1;

Plot[{f1[x],f1' [x]},{x,-4,4},PlotStyle->{GrayLeve1[0.01],Dashing[{0.01}]}]

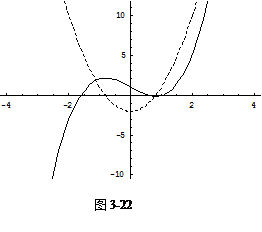则输出（如图3-22）.

图中的虚线是导函数的图形. 观察函数的增减与导函数的正负之间的关系.

再输入Solve[f1 ' [x]==0,x] , 则输出

        即得到导函数的零点. 用这两个零点,把导函数的定义域分为三个区间. 因为导函数连续,在它的两个零点之间,导函数保持相同符号.因此,只需在每个小区间上取一点计算导数值,即可判定导数在该区间的正负,从而得到函数的增减. 输入f1' [-1]；f1' [0]；f1' [1]；输出为1,-2,1.说明导函数在区间上分别取+,-和+. 因此函数在区间和上单调增加, 在区间上单调减少.

例3.2  求函数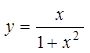的极值.

输入f2[x_]:=x/(1+x^2);

Plot[f2[x],{x,-10,10}]

则输出（如图3-23）.

观察它的两个极值.再输入Solve[f2'[x]==0,x]；

则输出{{x->-1},{x->1}}即驻点为用二阶导数判定极值,

输入   f2''[-1]；f2'' [1]  ,则输出1/2与-1/2.

因此是极小值点, 是极大值点.为了求出极值,再输入f2[-1]；f2[1]

输出-1/2与1/2. 即极小值为-1/2,极大值为1/2.

例3.3求曲线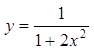的凹凸区间和拐点.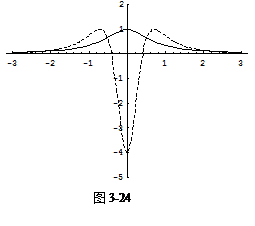

输入  f3[x_]:=1/(1+2x^2);

Plot[{f3[x],f3''[x]},{x,-3,3},PlotRange->{-5,2},

PlotStyle->{GrayLeve1[0.01],Dashing[{0.01}]}] , 输出（如图3-24）, 

其中虚线是函数的二阶导数. 观察二阶导数的正负与曲线的凹凸之间的关系.

再输入gen=Solve[f3'' [x]==0,x] , 则输出    

即得到二阶导数等于0的点是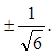 用例1中类似的方法知在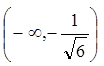和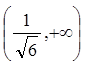上二阶导数大于零, 曲线弧向上凹. 在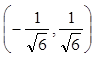上二阶导数小于零, 

曲线弧向上凸.再输入f3[x]/.gen；则输出{3/4,3/4}

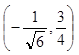这说明函数在和的值都是3/4. 因此两个拐点分别是和.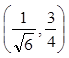

例3.4  已知函数

在区间上画出函数的图形, 并找出所有的驻点和拐点.

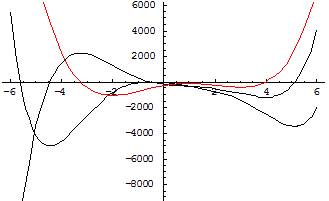
输入命令     f[x_]=x^6/2-2*x^5-25*x^4/2+60*x^3-150*x^2-180*x-25;

      Plot[{f[x],f' [x],f '' [x]},{x,-6,6},

     PlotStyle->{GrayLevel[0],Dashing[{0.01'}],RGBColor[1,0,0]}];

     NSolve[f' [x]==0, x]NSolve[f '' [x]==0,x];

则输出（如图3-25）