一、慕课视频（来自西安电子科技大学郭宝龙教授《工程信号与系统》慕课）

二、重点概念

拉普拉斯变换的概念

常见函数的拉普拉斯变换

三、知识要点

一）线性性质

若  f1(t)←→F1(s)          f2(t)←→F2(s)   

则      a1f1(t)+a2f2(t)←→a1F1(s)+a2F2(s)  

二）尺度变换

若f(t) ←→ F(s) ,    且有实数a>0 ，则f(at) ←→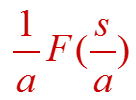

三） 时移特性

若 f(t) <----->F(s) ,   有实常数t0>0 ,

则 f(t-t0)(t-t0)<----->e-st0F(s)  

四）复频移特性

若f(t) ←→F(s) , 且有复常数sa=σa+jωa,

则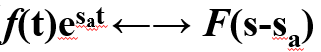

五）时域微分定理

若 f(t) ←→ F(s) ,  

则 f’(t) ←→ sF(s) – f(0-)    

六）时域积分

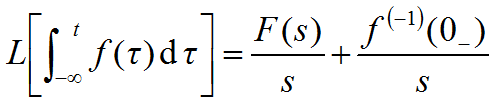
七）卷积定理

若因果函数  f1(t)←→ F1(s) ,

                         f2(t)←→ F2(s) ,

  则         f1(t)*f2(t)←→ F1(s)F2(s)

八）初值定理

设F(s)为真分式(若F(s)为假分式则化为真分式)，则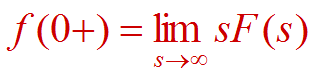 

九）终值定理

若f(t)当t →∞时存在，则 

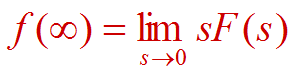
四、上课PPT

五、课后作业

5.1（4）

5.2（b)

5.3（11）（12）

5.4（1）