函数（Function）

函数是数学中用于描述变量之间关系的基础概念。在最简单的形式中，函数f 是一个规则，它将输入（或自变量）\( x \)映射到输出（或因变量）\( f(x) \)。

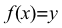
例如，线性函数f(x) = 2x + 1 描述了x 和 y 之间的线性关系。

导数（Derivative）

导数是用于描述函数在某一点处的局部行为或变化率的数学工具。对于函数\( f(x) \)，其在\( x = a \)处的导数通常表示为\( f'(a) \)或\( \frac{df}{dx} \)。

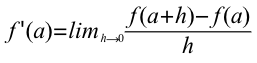
例如，函数 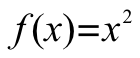 在x = 2 处的导数是 f'(2) = 4 ，表示当 x在2附近变化时， f(x) 以4的速度变化。

1. 函数和导数是物理、工程、经济学等多个领域的基础概念，用于描述自然现象和社会现象。

2. 在计算机科学中，导数（特别是偏导数和梯度）在优化算法和机器学习模型（如神经网络）中有广泛应用。

3. 函数和导数是微积分和数学分析的核心概念，对数学的发展有着重要影响。

函数和导数是数学和科学的基础概念，它们在理解和描述变量间复杂关系方面具有重要作用。

从自然科学到社会科学，再到现代的数据科学和人工智能，函数和导数都有着广泛和深远的应用。