实际问题:
水果店内有两种水果,价格分别是苹果2元/千克;香蕉3元/千克。一共要买70kg苹果和80kg香蕉。问:总共需要花费多少钱?
通常计算方式:
通用计算公式是 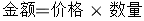
根据上式 
基于向量的表示
将两种水果的价格组成一组:(2,3),这组数的第1个是苹果的价格,第2个是香蕉的价格;把采购数量也组成一组:(70, 80),第1个数是苹果的数量,第2个数是香蕉的数量。
在数学上把这样组成一组的数称之为“向量(vector)”,这组数的第几个数成为这个向量的第几”分量(component)”,向量分量的个数是向量的“维度(dimension)”。
价格向量: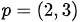
数量向量: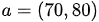
金额仍然是价格与数量的乘积,只不过总金额是两个向量的点积:
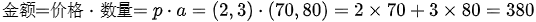
两个向量的点积(或内积)是两向量各分量的乘积之和,这是高中的知识,也是线性代数中也很常见。
向量思维,是用向量把一组数看作一个整体,把握整体关系,而非内部细节,从而简化问题。
| 水果 | 价格 | 数量 | 金额 |
| 苹果 | 2 | 70 | 2*70=140 |
| 香蕉 | 3 | 80 | 3*80=240 |
| 合计 | 380 |
我们可以用表格来形象理解向量思维,将“列”作为一个整体来表达计算关系,“价格列”乘以“数量列”等于“金额列”,“金额列”各项合计就是订单的销售金额。
NumPy科学计算包
NumPy(Numerical Python)是Python的一种开源的数值计算扩展包,目前已经成为使用Python进行科学计算的基础软件包。对NumPy的详细说明可以参看NumPy中文网。
NumPy提供了一个强大的多维数组对象(array),可以高效地进行数值计算、数据操作和数学运算。 使用NumPy前需要导入numpy模块,按惯例使用np的模块别名引用模块内的变量和函数。

根据我们上一章学习的面向对象编程的内容,使用NumPy包中的函数和模块,可以使用.的形式,例如从NumPy里引入π的数值:
NumPy使用数组(array)对象表达向量。

这条语句是使用函数np.array将一个列表[2, 3]创建成一个“一维数组”对象,作为价格向量p。
同样,创建一个一维数组作为数量向量a。

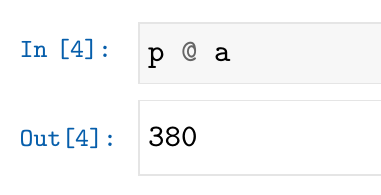
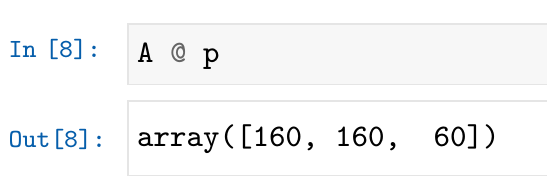
Python中使用运算符“@”表示向量乘法(点积),所以上面的计算在Python中就是
需要注意的是,Python中的向量除了点积乘法“@”之外,还有“算术运算”乘法“*”。点积运算是向量与向量层面的运算;而“算术运算”乘法实际是向量内各分量层面的乘法。例如下面,向量各分量的乘法:
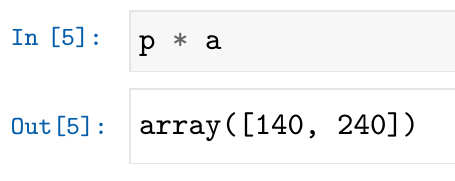
可以看到p和a两个向量相乘后得到的还是一个向量,也就是说向量p与向量a的各分量逐一的进行相乘。向量分量的“算术运算”除了乘法外,还可以进行作为分量的数所能进行一切运算,如加“+”、减“-”、乘“*”、除“/”、整除“//”、取模“%”、幂“**”以及各类函数。向量分量的“算术运算”,需要对每个分量逐个进行计算,因此参与运算的两向量维度相同,计算后也是一个同维度的向量。而对于向量点积,参与计算的两个向量也必须相同维度,但得到一个数。
如果对向量算术乘法得到的向量各分量求和,那么会得到和向量点积一样的结果。
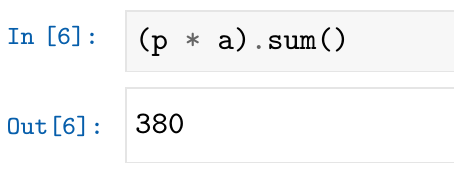
上面程序,向量算术乘法 后得到的向量,调用这个向量(数组对象)的sum()方法,可以计算这个向量各分
量的和,结果和
后得到的向量,调用这个向量(数组对象)的sum()方法,可以计算这个向量各分
量的和,结果和 是一样的。
是一样的。
基于矩阵表示
向量是一组数,矩阵(matrix)要比向量复杂一些,矩阵是由“一组向量”构成,可以看作“向量”的“向量”,而不仅是一组数。上一节的例子中,分3个批次购买水果,如下表所示:
| 批次 | 苹果 | 香蕉 |
| 第1批 | 20 | 40 |
| 第2批 | 35 | 15 |
| 第3批 | 15 | 25 |
| 合计 | 70 | 80 |
第1批数量向量 (20, 40),第 2 批数量向量(35,15),第3批数量向量(15,25), 这三个向量构成一个“订单采购批次”矩阵,A,矩阵很像一个抽象的表格。
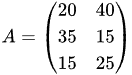
数组(array)对象也可以用来表示矩阵。就如,用一维数组表示一组数的向量,可以用一维数组的数组,用二维数组来表示矩阵一维向量的向量。

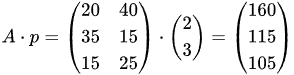
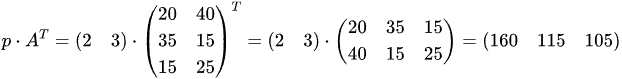

价格组合方案
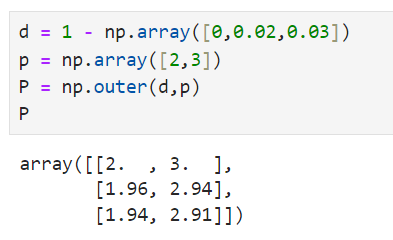
如果可以有两个等级的折扣可以执行1%和3%,根据折扣公式:折后价格 = (1-折扣)X 价格 。可以计算出一个折扣向量:

标量(数)1减了一个3维的向量,这是numpy的“广播(broadcast)”机制,这里将一个标量自动扩展成一个向量,其各分量都是1,实际的运算是“np.array([1,1,1])-np.array([0, 0.02, 0.03])”。 价格组合方案是将折扣向量和价格向量进行组合,各种折扣与各类货品的两两组合,这种组合操作可以使用“外积”的向量运算,两两分量进行内积的组合,如果分量是一个实数标量而用乘法。
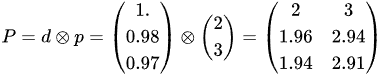
numpy使用函数np.outer()计算两个向量的外积。