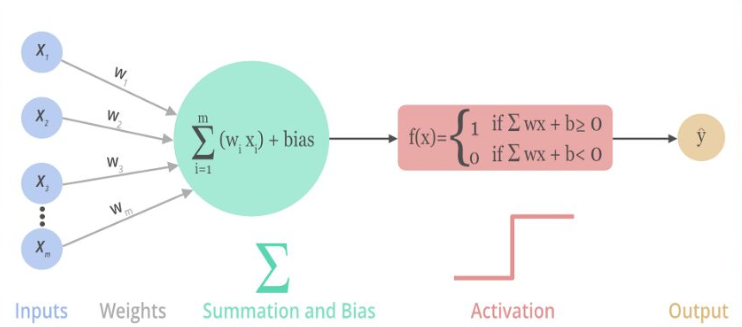
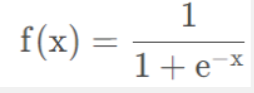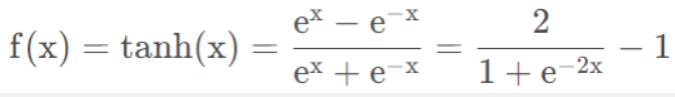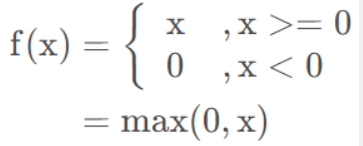多层感知器回归器。
该模型使用 LBFGS 或随机梯度下降优化平方误差。
class sklearn.neural_network.MLPRegressor(hidden_layer_sizes=(100,), activation='relu', *,
solver='adam', alpha=0.0001, batch_size='auto', learning_rate='constant', learning_rate_init=0.001,
power_t=0.5, max_iter=200, shuffle=True, random_state=None, tol=0.0001, verbose=False,
warm_start=False, momentum=0.9, nesterovs_momentum=True, early_stopping=False,
validation_fraction=0.1, beta_1=0.9, beta_2=0.999, epsilon=1e-08, n_iter_no_change=10,
max_fun=15000)
参数:
‘constant’ 是由‘learning_rate_init’ 给出的恒定学习率。
‘invscaling’ 在每个时间步 ‘t’ 使用 ‘power_t’ 的逆缩放 index 逐渐降低学习率 learning_rate_。 effective_learning_rate = learning_rate_init /pow(t, power_t)
‘adaptive’ 保持学习率恒定为 ‘learning_rate_init’ 只要训练损失不断减少。如果 ‘early_stopping’ 开启,每次连续两个 epoch 未能将训练损失减少至少 tol 或未能将验证分数增加至少 tol 时,当前学习率除以 5。
‘lbfgs’ 是quasi-Newton 方法系列中的优化器。
‘sgd’ 指的是随机梯度下降。
‘adam’ 指的是由 Kingma、Diederik 和 Jimmy Ba 提出的基于随机梯度的优化器
‘identity’, no-op 激活,用于实现线性瓶颈,返回 f(x) = x
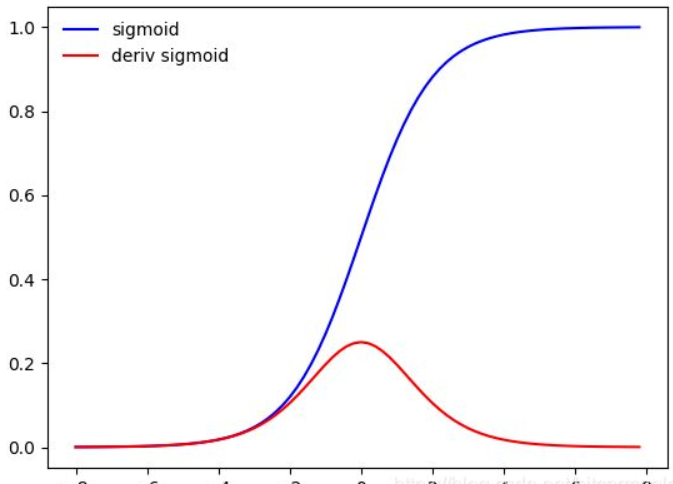
‘logistic’,逻辑 sigmoid 函数,返回 f(x) = 1 /(1 + exp(-x))。
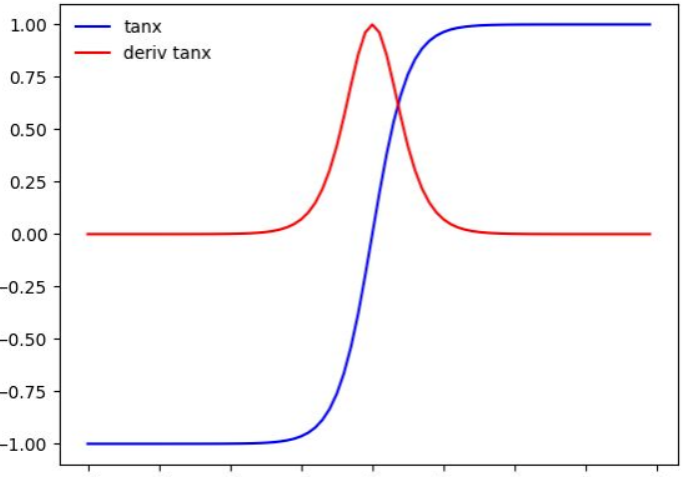
‘tanh’,双曲 tan 函数,返回 f(x) = tanh(x)。
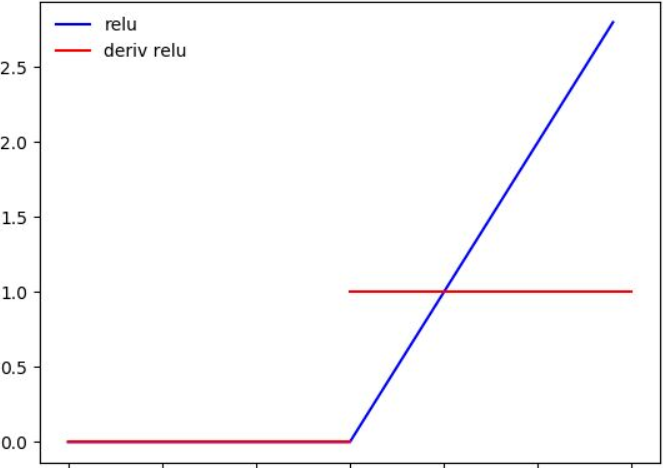
‘relu’,整流后的线性单位函数,返回 f(x) = max(0, x)
hidden_layer_sizes:元组,长度= n_layers - 2,默认=(100,)
第 i 个元素表示第 i 个隐藏层中的神经元数量。
activation:{‘identity’, ‘logistic’, ‘tanh’, ‘relu’},默认='relu'
隐藏层的激活函数。
solver:{‘lbfgs’, ‘sgd’, ‘adam’},默认='adam'
权重优化的求解器。
注意:就训练时间和验证分数而言,默认求解器 ‘adam’ 在相对较大的数据集(具有数千个训练样本或更多)上运行良好。然而,对于小型数据集,‘lbfgs’ 可以更快地收敛并表现更好。
alpha:浮点数,默认=0.0001
L2 惩罚(正则化项)参数。
batch_size:整数,默认='自动'
随机优化器的小批量大小。如果求解器是‘lbfgs’,分类器将不使用小批量。当设置为 “auto”、batch_size=min(200, n_samples) 时。
learning_rate:{‘constant’, ‘invscaling’, ‘adaptive’},默认='常量'
权重更新的学习率计划。
仅在solver='sgd'时使用。
learning_rate_init:浮点数,默认=0.001
使用的初始学习率。它控制step-size 更新权重。仅在solver='sgd' 或‘adam’ 时使用。
power_t:浮点数,默认=0.5
逆缩放学习率的 index 。当learning_rate设置为‘invscaling’时,它用于更新有效学习率。仅在solver='sgd'时使用。
max_iter:整数,默认=200
最大迭代次数。求解器迭代直到收敛(由‘tol’ 确定)或此迭代次数。对于随机求解器 (‘sgd’, ‘adam’),请注意,这决定了 epoch 的数量(每个数据点将被使用多少次),而不是梯度步骤的数量。
shuffle:布尔,默认=真
是否在每次迭代中打乱样本。仅在solver='sgd' 或‘adam’ 时使用。
random_state:int,RandomState 实例,默认=None
确定权重和偏差初始化的随机数生成,train-test 如果使用提前停止,则拆分,当solver='sgd' 或‘adam’ 时进行批量采样。传递一个 int 以获得跨多个函数调用的可重现结果。请参阅词汇表。
tol:浮点数,默认=1e-4
优化的容差。当 n_iter_no_change 连续迭代的损失或分数没有提高至少 tol 时,除非将 learning_rate 设置为 ‘adaptive’,否则认为达到收敛并停止训练。
verbose:布尔,默认=假
是否将进度消息打印到标准输出。
warm_start:布尔,默认=假
当设置为 True 时,重用之前调用的解决方案作为初始化,否则,只需擦除之前的解决方案。请参阅词汇表。
momentum:浮点数,默认=0.9
梯度下降更新的动量。应介于 0 和 1 之间。仅在solver='sgd' 时使用。
nesterovs_momentum:布尔,默认=真
是否使用涅斯捷罗夫的动量。仅在求解器 ='sgd' 且动量 > 0 时使用。
early_stopping:布尔,默认=假
当验证分数没有提高时,是否使用提前停止来终止训练。如果设置为 true,它将自动留出 10% 的训练数据作为验证,并在连续 n_iter_no_change 的验证分数没有提高至少 tol 时终止训练。仅在solver='sgd' 或‘adam’ 时有效。
validation_fraction:浮点数,默认=0.1
留出作为提前停止验证集的训练数据的比例。必须介于 0 和 1 之间。仅在 early_stopping 为 True 时使用。
beta_1:浮点数,默认=0.9
在 adam 中估计一阶矩向量的 index 衰减率应该在 [0, 1) 中。仅在solver='adam'时使用。
beta_2:浮点数,默认=0.999
在 adam 中估计二阶矩向量的 index 衰减率应该在 [0, 1) 中。仅在solver='adam'时使用。
epsilon:浮点数,默认=1e-8
亚当数值稳定性的值。仅在solver='adam'时使用。
n_iter_no_change:整数,默认=10
不满足tol 改进的最大时期数。仅在solver='sgd' 或‘adam’ 时有效。
max_fun:整数,默认=15000
仅在求解器='lbfgs' 时使用。函数调用的最大数量。求解器迭代直到收敛(由‘tol’ 确定),迭代次数达到max_iter,或此函数调用次数。请注意,函数调用的数量将大于或等于 MLPRegressor 的迭代次数。
属性:
loss_:浮点数
使用损失函数计算的当前损失。
best_loss_:浮点数
求解器在整个拟合过程中达到的最小损失。
loss_curve_:形状列表(n_iter_,)
在每个训练步骤结束时评估的损失值。列表中的第 i 个元素表示第 i 次迭代的损失。
t_:int
求解器在拟合期间看到的训练样本数。数学上等于n_iters * X.shape[0],意思是time_step,它被优化器的学习率调度器使用。
coefs_:形状列表 (n_layers - 1,)
列表中的第 i 个元素代表第 i 层对应的权重矩阵。
intercepts_:形状列表 (n_layers - 1,)
列表中的第 i 个元素表示对应于第 i + 1 层的偏置向量。
n_features_in_:int
拟合期间看到的特征数。
feature_names_in_:ndarray 形状(n_features_in_,)
拟合期间看到的特征名称。仅当 X 具有全为字符串的函数名称时才定义。
n_iter_:int
求解器已运行的迭代次数。
n_layers_:int
层数。
n_outputs_:int
输出数量。
out_activation_:str
输出激活函数的名称。
注意:
MLPRegressor 迭代训练,因为在每个时间步都会计算损失函数相对于模型参数的偏导数以更新参数。
它还可以在损失函数中添加一个正则化项,以缩小模型参数以防止过度拟合。
此实现适用于表示为密集和稀疏 numpy 浮点值数组的数据。
案例举例1:
from sklearn.neural_network import MLPRegressor
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
X, y = make_regression(n_samples=200, random_state=1)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
regr = MLPRegressor(random_state=1, max_iter=500).fit(X_train, y_train)
regr.predict(X_test[:2])
array([-0.9..., -7.1...])
regr.score(X_test, y_test)
0.4...
案例举例2:
使用 MLPRegressor 拟合 3D 函数
def threeDFunc(xin,yin):
z = np.zeros((40,40))
for xIndex in range(0,40,1):
for yIndex in range(0,40,1):
z[xIndex,yIndex]=(np.exp(-(xin[xIndex]**2+yin[yIndex]**2)/0.1))
return z
xThD = np.arange(-1,1,0.05)
yThD = np.arange(-1,1,0.05)
zThD = threeDFunc(xThD, yThD)

classifier = neural_network.MLPRegressor(hidden_layer_sizes=(200, 200),
activation='logistic', learning_rate='adaptive')
xy = np.array((xThD.flatten(),yThD.flatten()))
classifier.fit(np.transpose(xy), zThD)
pre = classifier.predict(np.transpose(xy))
import pylab
from mpl_toolkits.mplot3d import Axes3D
fig = pylab.figure()
ax = Axes3D(fig)
X, Y = np.meshgrid(xThD, yThD)
ax.plot_wireframe(X, Y, zThD)
ax.plot_wireframe(X, Y, pre, color='red')
print(np.shape(zThD))
print(np.shape(pre))
plt.show()
使用 activation='tanh'
将激活函数更改为双曲 tan 函数,使用 solver='lbfgs' 将求解器更改为 lbfgs。
如果分类器实例化如下所示,则红色和蓝色的图应该几乎相同:
classifier = neural_network.MLPRegressor(hidden_layer_sizes=(200, 200),
solver='lbfgs', activation='tanh', learning_rate='adaptive')