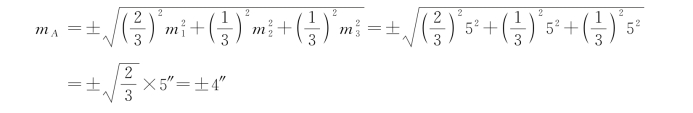误差传播定律

一、观测值的函数

在测量工作中，有些未知量往往不能直接测得，而是由某些直接观测值通过一定的函数关系间接计算得到。例如，水准测量中，测站高差是由前、后视读数求得的，即h=a-b。式中高差h是直接观测值a、b的函数；又如三角高程测量中，高差h是由直接观测值水平距离、竖直角、仪器高、目标高推算得到，函数关系式如下：h=D tanα+i-v。水准测量计算高差的函数式为线性函数式，而三角高程测量计算高差的函数式为非线性函数式。两种函数的一般表达式如下。

1.线性函数

线性函数的一般形式为

式中：x 1，x 2，…，x n为独立观测值，k 1，k 2，…，k n为常数。

2.非线性函数

非线性函数即一般函数，其形式为

对函数取全微分

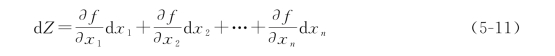
因为真误差很小，可用真误差Δx i代替d x i，得真误差关系式：

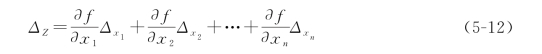
式中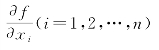：为函数对各自变量所取的偏导数。

二、函数的中误差

由于直接观测值存在误差，函数也受其影响而产生误差。阐述观测值中误差与函数中误差关系的定律，称为误差传播定律。下面按线性函数与非线性函数两种情况分别进行讨论。

1.线性函数的中误差

线性函数的一般形式

其真误差关系式为

若对x 1，x 2，…，x n均观测n次，则可得

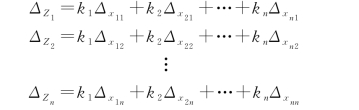
将上面式子平方后求和，再除以n，则得

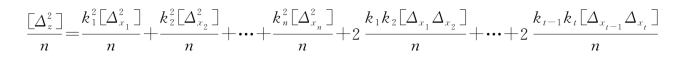
由于Δx 1，Δx 2，…，Δx n均为独立观测值的偶然误差，所以其乘积Δx iΔx i+1也必然呈现偶然性。

设函数Z的中误差为m Z，根据偶然误差特性和中误差的定义，当n→∞时，可得

式中：m 1，m 2，…，m n分别为各观测量的中误差。

2.非线性函数的中误差

非线性函数Z=f（x 1，x 2，…，x n）的真误差关系式为

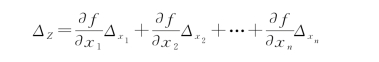
其中偏导数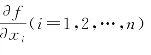为常数，因此，仿照式（5-13），得函数Z的中误差为

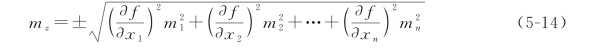
可将线性函数看成非线性函数的一种特例，也可以写出线性函数的全微分式，其系数k不变。

三、应用实例

【例题5-2】 自水准点BM 1向水准点BM 2进行水准测量（图5-3），设各段所测高差分别为h 1=+3.852m±5mm；h 2=+6.305m±3mm；h 3=-2.346m±4mm，求BM 1、BM 2两点间的高差及中误差（其中，后缀±5mm、±3mm、±4mm为各段观测高差的中误差）。

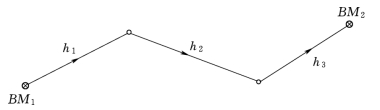
图5-3　水准测量平差

解：（1）列函数式。BM 1、BM 2之间的高差h=h 1+h 2+h 3=7.811m，即两点间的高差为7.811m。

（2）写出函数的真误差与观测值真误差的关系式。Δh=Δh 1+Δh 2+Δh 3，可见各系数k 1、k 2、k 3均为1。

（3）高差中误差

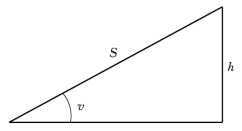
图5-4　三角形观测

【例题5-3】 在三角形（图5-4）中，测得斜边S为100.000m，其观测中误差为3mm，观测得竖直角v为30°，其测角中误差为3″，求高差h的中误差。

解：（1）列函数式：h=S sin v。

（2）写出函数的真误差与观测值真误差的关系式。由于是非线性函数，则先写出全微分式：

d h=sin v d s+S cos v d v

再写出真误差的关系式：Δh=sin vΔs+S cos vΔv=（sin30°）Δs+100cos（30°）Δv

（3）求高差中误差：

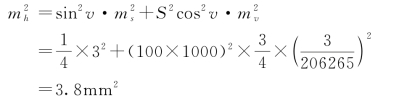
则中误差：m h=±1.95mm

【例题5-4】 以同精度观测了一个三角形的3个内角L 1、L 2、L 3，其中误差均为5″，且各观测值之间互相独立，求将三角形闭合差平均分配后的角A的中误差。

解：（1）列函数式：闭合差W=L 1+L 2+L 3-180°。

平均分配后的角（由于L 1与W互相不独立，故对该式要进一步转换）

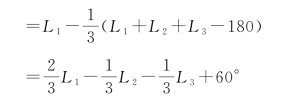
（2）写出函数的真误差与观测值真误差的关系式：

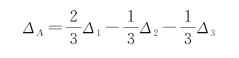
（3）高差中误差：