观测值的精度评定

观测量（如角度、距离、两点间的高差等）的真值无法得知，只有经过多次重复测量，经过平差计算才能得到近似于真值的可靠值，称为平差值，常用符号L^表示。

在相同的观测条件下进行的观测，称为等精度观测。在不同的观测条件下进行的观测，称为非等精度观测。下面介绍等精度观测平差值计算及精度评定。

一、等精度观测的平差值计算

设在相同的观测条件下，对某未知量X进行了n次观测，观测值为L 1，L 2，…，L n

将式（5-15）求和后除以n，得

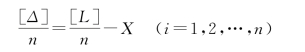
当n→∞时，根据偶然误差的特性，有

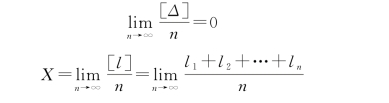
即当n趋近无穷大时，算术平均值为真值。

在实际工作中观测次数有限，所以算术平均值不可视为所求量的真值；但随着观测次数的增加，算术平均值是趋近于真值，认为是该值的最可靠值，即平差值。

结论：等精度观测的平差值等于这些观测值的算术平均值。

二、等精度观测的精度评定

（一）中误差的计算

前面给出了等精度观测的中误差计算公式：

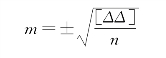
式中：Δ为观测值的真误差。

真值X有时是知道的（例如三角形3个内角之和的真值为180°），但更多情况下，真值是不知道的。因此，真误差也无法知道，不能直接用上式求出中误差。但是根据前述，可以求得观测值的平差值，平差值与观测值之差称为改正数v i，即

实际工作中可以利用观测值的改正数来计算观测值的中误差。推导如下

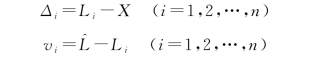
将上两式合并得

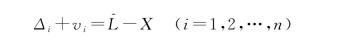
令

则

得出

上式等号两边平方求和再除以n，得

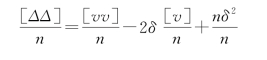
由于［v］=0，有

其中

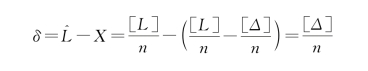
则

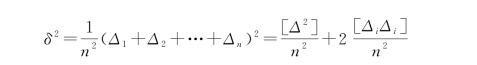
当n→∞时，上式右端第二项趋于0，则

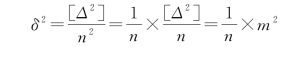
将上式代入式（5-17）得

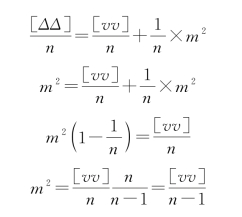
则

式（5-18）为同精度观测中用观测值的改正数计算观测值中误差的公式，称为白塞尔公式。

【例题5-5】 对一段距离进行5次观测，其观测结果见表5-3，求该组距离观测值的中误差。

表5-3　距离观测及中误差计算

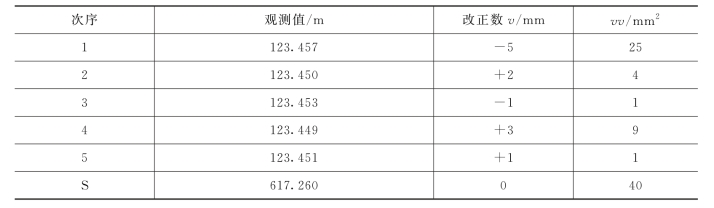
解：各观测值的改正数具体数值见表5-3

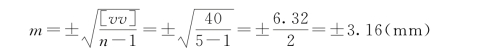
（二）等精度观测平差值的精度评定

由前述可知，等精度观测的平差值就是算术平均值，要评定它的精度，可以把算术平均值看成是各个观测值的线性函数。

【例题5-6】 算术平均值已知各观测值的中误差为m 1=m 2=…=m n=m，求算术平均值（平差值）的中误差。

解：对算术平均值的表达式求全微分：

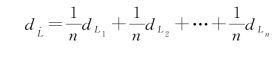
根据误差传播定律有

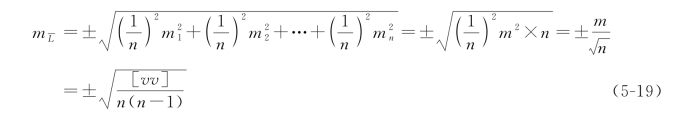
【例题5-7】 已知各三角形内角和见表5-4，求测角中误差m。

表5-4　三角形内角和观测值及中误差计算表

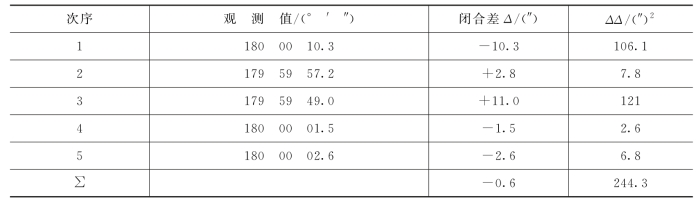
解：先计算出各三角形闭合差（表5-4），再利用真误差求三角形闭合差的中误差（即函数值的中误差），得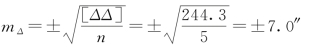

列函数式：真误差（闭合差）Δ=A+B+C-180°（其中3个内角A、B、C为等精度观测，则m A=m B=m c=m）

根据误差传播定律得

现已算得mΔ为±7.0″，需求出m，即为传播律的逆向使用。

测角中误差