测量误差及其分类

测量实践表明，在一定的外界条件下对同一量进行多次观测，不论观测者使用多么精密的仪器和工具、采用多么合理的观测方法、观测多么精细，其观测结果总会存在差异。这种差异说明了观测中存在误差，而且观测误差的产生是不可避免的。本章主要介绍产生误差的基本原因、误差的性质、观测成果质量的评判标准以及误差传播定律等。

一、测量误差及来源

任何观测值都包含误差，例如，闭合水准路线的高差闭合差往往不等于0，说明观测值中有误差存在。观测对象客观存在的量，称为真值，通常用X表示，例如三角形内角和的真值为180°。每次观测所得的数值，称为观测值，通常用L i（i=1，2，…，n）表示。观测值与真值的差值，称为真误差，也称为观测误差，通常用Δi表示，有

产生观测误差的因素是多方面的，主要概括为3个方面：

（1）观测时由于观测者感觉器官的鉴别能力存在局限性，在仪器的对中、整平、照准、读数等方面都会产生误差。同时，观测者的技术熟练程度也会对观测结果产生一定影响。

（2）测量中使用的仪器和工具，在设计、制造、安装和校正等方面不可能十分完善，同时仪器的精度有限，致使测量结果产生误差。

（3）观测过程中的外界条件（如温度、湿度、风力、阳光、大气折光等）时刻都在变化，必将对观测结果产生影响。

通常把上述的人、仪器、客观环境这3种因素综合起来称为观测条件。

因受上述因素的影响，测量中存在误差是不可避免的。但是误差与粗差是不同的，粗差是指观测结果中出现的错误，如测错、读错、记错等，通常“测量误差”不包括粗差。凡含有粗差的观测值应舍去，并需重测。

测量中，一般把观测条件相同的各次观测，称为等精度观测；观测条件不同的各次观测，称为非等精度观测。

二、测量误差的分类

根据观测误差的性质不同，观测误差分为系统误差和偶然误差两类。

1.系统误差

在相同观测条件下，对某观测量进行一系列观测，若出现的误差在数值、符号上保持不变或按一定的规律变化，这种误差称为系统误差。

系统误差是由仪器制造或校正不完善、观测者生理习性及观测时的外界条件等原因引起的。例如，用名义长度为30m而实际长度为30.003m的钢卷尺量距，每量一尺段就有3mm的误差。这种量距误差，其数值和符号不变，且量的距离越长，误差越大。因此，系统误差在观测成果中具有累计性。

系统误差的特性有同一性，单向性，累积性。

系统误差在观测成果中的累积性，对成果质量影响显著。因其符号和大小有一定的规律性，如能找到规律，可在观测中采取相应措施，消除或削弱系统误差的影响。

系统误差消除的方法如下：

（1）测量仪器误差，对观测结果加以改正。例如进行钢尺检定，求出尺长改正数，对量取的距离进行尺长改正。

（2）测前对仪器进行检校，以减少仪器校正不完善的影响。例如水准仪的i角检校，使其影响减到最小限度。

（3）采用合理观测方法，使误差自行抵消或削弱。例如，水平角观测中，采用盘左、盘右观测，可消除视准轴误差；水准尺的零点误差可以通过偶数站到达来消除。

2.偶然误差

在相同观测条件下，对某观测量进行一系列观测，若出现的误差在数值、符号上有一定的随机性，从表面看并没有明显的规律性，但从大量误差的总体而言，具有一定的统计规律，这种误差称为偶然误差。如用全站仪测角时的照准误差；水准测量中，在标尺上读数时的估读误差等。通过多次观测取平均值的方法可以削弱偶然误差的影响，但是不能完全消除偶然误差的影响。

为了提高观测成果的质量、发现和消除错误，在测量工作中，一般都要进行多于必要的观测，称多余观测。例如，测量一平面三角形的三个内角，以便检校内角和，从而判断结果的正确性。

三、偶然误差的特性

偶然误差产生的原因是随机性的，只有通过大量观测才能揭示其内在的规律，观测次数越多，规律性越明显。

假如在相同的观测条件下，独立观测了358个三角形的3个内角，每个三角形内角之和应等于180°，由于观测值存在误差而往往不相等。根据式（5-1）可计算各三角形内角和真误差（在测量工作中称为三角形闭合差）

式中：（L 1+L 2+L 3）i为第i个三角形内角观测值之和。

现取误差区间的间隔dΔ=3″，将这一组误差按其正负号与误差值的大小排列。出现在基本区间误差的个数称为频数，用K表示，频数除以误差的总个数n得到的值称为频率（K/n），也称相对个数。统计结果见表5-1。

表5-1　多次观测结果中偶然误差在区间出现个数统计表

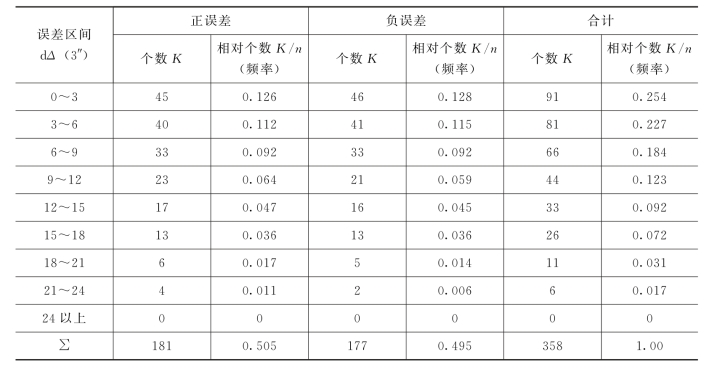
由表5-1中可以看出：小误差出现的频率较大，大误差出现的频率较小；绝对值相等的正负误差出现的频率相当；绝对值最大的误差不超过某一个定值。其他测量结果也显示出上述规律。因此偶然误差具有如下特性：

（1）在一定的观测条件下，偶然误差的绝对值不会超过一定的限值。

（2）绝对值小的误差比绝对值大的误差出现的机会多。

（3）绝对值相等的正负误差出现的机会相等。

（4）偶然误差的算术平均值随观测次数的无限增加而趋向于0，即

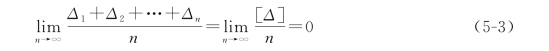
式中：［Δ］为误差总和。

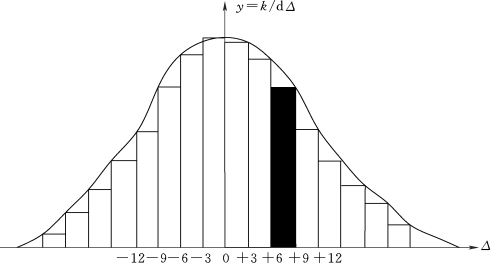
图5-1　频率直方图

为了充分反映误差分布的情况，除了用上述表格的形式（误差分布表）表示，还可以用直观的图形来表示。如图5-1所示，以横坐标表示误差的大小，纵坐标表示各区间误差出现的相对个数除以区间的间隔值。这样，每一误差区间上方的长方形面积，就代表误差出现在该区间的相对个数。例如图中有阴影的长方形面积就代表误差出现在+6″～+9″区间内的相对个数为0.092。这种图称为直方图，其特点是能形象地反映出误差的分布情况。

如果继续观测更多的三角形，即增加误差的个数，当n→∞时，各误差出现的频率趋近于一个完全确定的值，这个数值就是误差出现在各区间的概率。此时如将误差区间无限缩小，那么图5-1中各长方条顶边所形成的折线将成为一条光滑的连续曲线，称为误差分布曲线，也叫正态分布曲线。曲线上任一点的纵坐标y均为横坐标Δ的函数，其函数形式为

式中：e为自然对数的底（e=2.7183）；σ为观测值的标准差，其几何意义是分布曲线拐点的横坐标，其平方σ2称为方差。

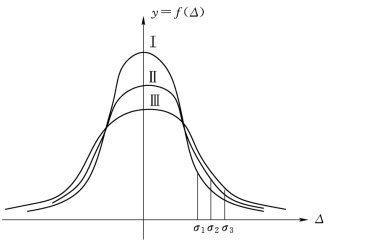
图5-2　三组观测分布曲线

如图5-2所示，有三条误差分布曲线Ⅰ、Ⅱ及Ⅲ，代表不同标准差σ1，σ2及σ3的三组观测。由图中看出，曲线Ⅰ较高而陡峭，表明绝对值较小的误差出现的概率大，分布密集；曲线Ⅱ、Ⅲ较低而平缓，分布离散。因此，前者的观测精度高，后两者则较低。由误差分布的密集和离散程度，可以判断观测的精度。