直线定向与坐标方位角计算

一、直线定向

要确定两点间平面位置的相对关系，除了需要测量两点间的距离，还要确定直线的方向。确定地面上一条直线与标准方向的角度关系的工作，称为直线定向。

（一）标准方向的种类

测量工作采用的标准方向有真子午线方向、磁子午线方向和坐标纵轴方向。

（1）真子午线方向。通过地面上某点作其所在的真子午线的切线，称为该点的真子午线方向，又称真北方向。

（2）磁子午线方向。磁针水平静止时其轴线所指的方向线，称为该点的磁子午线方向。

（3）坐标纵轴方向。坐标纵轴方向就是平面直角标系中的纵坐标轴方向。若采用高斯平面直角坐标，则以中央子午线作为坐标纵轴。

真子午线方向、磁子午线方向和坐标纵轴方向合称为标准方向，它们的北方向称为三北方向，如图6-4所示。

（二）直线方向的表示方法

表示直线方向的方式有方位角与象限角两种，其中，象限角应用较少，通常作为方位角推算的中间变量。

（1）方位角。由标准方向的北端起，顺时针方向量至某直线的角度，称为该直线的方位角，角值为0°～360°，如图6-5所示。根据采用的标准方向是真子午线方向、磁子午线方向和纵坐标轴方向，测定的方位角分别称为真方位角、磁方位角和坐标方位角，相应地用α真、α磁和α来表示。

（2）象限角。某直线与坐标纵轴所夹的锐角称为象限角，一般用R表示。由于象限角为锐角，与所在象限有关，因此描述象限角时，不但要注明角度的大小，还要注明所在的象限。如图6-6所示，北东R 1、南东R 2、南西R 3、北西R 4分别为四条直线的象限角。

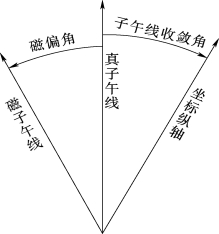
图6-4　三北方向线

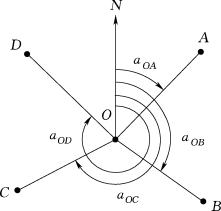
图6-5　方位角

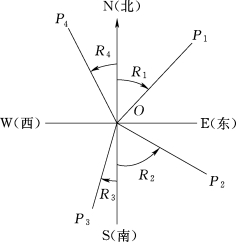
图6-6　象限角

（3）方位角与象限角的关系。根据方位角与象限角的定义，它们之间的换算关系见表6-5。

表6-5　方位角、象限角与坐标增量的关系

（三）三种方位角之间的关系

（1）真方位角与磁方位角的关系。地磁南北极与地球南北极并不重合，因此，过地面上某点的磁子午线与真子午线不重合，其夹角δ称为磁偏角，如图6-7所示。磁针北端偏于真子午线以东称东偏，偏于以西称西偏。直线的真方位角与磁方位角可按式（6-1）换算，式中δ值，东偏时取正值，西偏时取负值

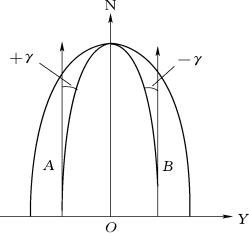
（2）真方位角与坐标方位角的关系。由高斯分带投影可知，除了中央子午线上的点，投影带内其他各点的坐标轴方向与真子午线方向都不重合，其夹角γ称为子午线收敛角，如图6-8所示。坐标轴方向北端偏于真子午线以东称东偏，偏于以西称西偏。真方位角与坐标方位角之间的关系可用式（6-2）换算，式中的γ值，东偏时取正值，西偏时取负值

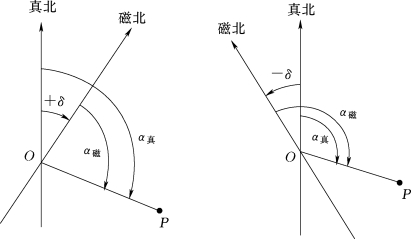
图6-7　真方位角与磁方位角的关系

（3）坐标方位角与磁方位角的关系。若已知某点的磁偏角δ与子午线收敛角γ，则坐标方位角与磁方位角之间的换算关系见式（6-3），式中的δ、γ值，东偏时取正值，西偏时取负值。

二、坐标方位角与推算

（一）正、反坐标方位角

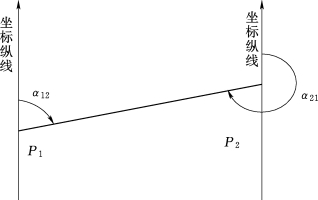
图6-9　直线的正反坐标方位角

地面上各点的真（磁）子午线方向都是指向地球（磁）的南北极，各点的子午线都不平行，给计算工作带来不便。而在平面直角坐标系中，纵坐标轴方向线均是平行的。因此在普通测量工作中，多数是以坐标方位角表示直线的方向。如图6-9所示，设直线P 1至P 2的坐标方位角a 12为正坐标方位角，则P 2至P 1的方位角α21为反坐标方位角，显然，正、反坐标方位角互差180°，见式（6-4）。当α21＞180°时，式（6-1）取“-”号，当α21＜180°时，取“+”号。

（二）坐标方位角推算

坐标方位角推算分以下两种情况。

1.共用顶点的坐标方位角推算

如图6-10所示，由AB方位角推算AC方位角时，观测角β为左角，而由AC方位角推算AB方位角时，观测角β为右角，推算公式如下：

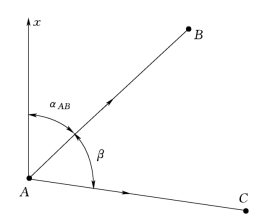
图6-10　共用顶点方位角推算

以上公式简称为“左加右减”。

左、右角的判别方法如下：人站在测站上，面向路线前进方向（即面向待求点方向），所测转折角位于观测者的左手边则称为左角，在观测者右手边则称为右角。

2.连续折线的方位角推算公式

如图6-11（a）所示，α12为已知方位角，转折角β2为右角，推算2—3边的方位角为

α23=α12+180°-β2

如图6-11（b）所示，α12为已知方位角，转折角β2为左角，推算2—3边的方位角为

α23=α12+β2-180°

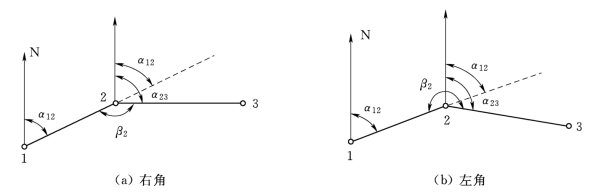
图6-11　折线方位角推算

因此，连续折线方位角推算时，要考虑转折角βi是左角还是右角，其通用公式为式（6-7）和式（6-8）。

式中：α后为转折前已知边的坐标方位角；α前为转折后待求边的坐标方位角；脚标“后”和“前”为前进方向的前后。

在推算过程中须注意：推算出的方位角α前若大于360°，应减去360°；若小于0°，应加上360°。

三、坐标增量计算

地面上两点的坐标值之差称为坐标增量，用Δx AB表示A点至B点的纵坐标增量，Δy AB表示A点至B点的横坐标增量。坐标增量有方向性和正负意义，Δx BA，Δy BA分别表示B点至A点的纵、横坐标增量，其符号与Δx AB，Δy AB相反。

1.根据两个点的坐标计算坐标增量

如图6-12所示，设A，B两点的坐标分别为A（x A，y A），B（x B，y B）。则A至B点的坐标增量为

而B至A点的坐标增量为

很明显，A点至B点与B点至A点的坐标增量，绝对值相等，符号相反。由于坐标方位角和坐标增量均有方向性（由下标表示），需注意下标的书写次序。

2.根据直线的坐标方位角和边长计算坐标增量

在图6-12中，设AB的坐标方位角为αAB，边长为D AB。则A点至B点的坐标增量为

四、坐标正算

根据已知点的坐标、观测边的长度及其坐标方位角计算待求点的坐标，称为坐标正算。如图6-13所示，假设已知点1的坐标为（x 1，y 1）和1—2边的坐标方位角α12，测得1—2边长D 12，则2点的坐标（x 2，y 2）计算公式为

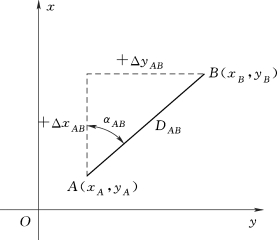
图6-12　坐标增量

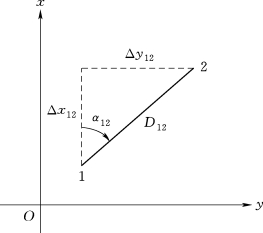
图6-13　坐标正算

式中：Δx 12、Δy 12为1—2边坐标增量

【例题6-1】 如图6-13所示，已知1—2边长为D 12=123.45m，方位角为α12=78°36′48″，1点坐标为（3145.67，4234.78）（单位：m），试求2点坐标。

解：

五、坐标反算

根据直线两端点坐标计算直线的边长和坐标方位角，称为坐标反算。

根据图6-13可知，假设1、2点坐标分别为（x 1，y 1）、（x 2，y 2），则可按以下步骤分别计算坐标方位角和边长：

首先由式（6-13）计算直线边的象限角，再根据坐标增量的符号判断其所在象限，按照表6-6方位角与象限角的关系计算其坐标方位角，然后按照式（6-14）计算边长。

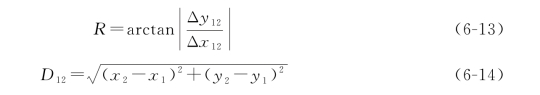
表6-6　方位角、象限角与坐标增量的关系

【例题6-2】 已知1、2点坐标分别为（4342.99，3814.29）、　（2404.50，525.72）（单位：m），试计算1—2边长及其坐标方位角。

解：

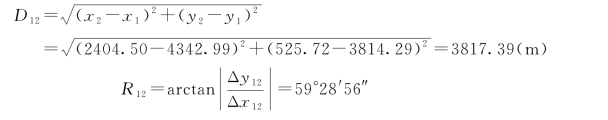
由于Δx 12＜0，Δy 12＜0，则α12=R 12+180°=239°28′56″